Федеральное агентство морского и речного транспорта Федеральное государственное бюджетное образовательное учреждение высшего образования

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОРСКОГО И РЕЧНОГО ФЛОТА

имени адмирала С. О. МАКАРОВА

ИНСТИТУТ ВОДНОГО ТРАНСПОРТА

Кафедра судостроения и энергетических установок

Курсовой проект

«Определение позиционных характеристик понтона»

по дисциплине «Вычислительный эксперимент в проектировании объектов морской (речной) техники»

Выполнил: студент группы М-11

Авцин. В.М.

Проверил: Афанасьев М.П.

Санкт-Петербург 2024

Оглавление

Введение 3

Создание геометрии. 4

Расчеты 5

0 градусов 5

10 градусов 9

20 градусов 10

30 градусов 11

45 градусов 12

90 градусов 13

Построение графиков зависимости позиционных характеристик от угла 𝜷 14

Вывод 16

Введение

При движении судна на корпусе возникают усилия, которые в безразмерном виде приведены к коэффициентам 𝐶_𝑥, 𝐶_𝑦, 𝐶_𝑀𝑧 (позиционным характеристикам).

Цель работы: спроектировать прямоугольный понтон и исследовать его позиционные характеристики в диапазоне углов от 0 до 90 градусов с помощью платформы для инженерного анализа SimScale.

Исходные данные:

Прямоугольный понтон с главными размерениями:

• L=1,885 м

• B=0,6 м

• T=0,067 Fn=0,15

Создание геометрии.

Для того чтобы исследовать позиционные характеристики прямоугольного понтона, необходимо создать его модель.

Это было выполнено в ПО «FreeCAD»

Рисунок 1 - Модель прямоугольного понтона

Далее в SimScale был добавлен Flow Region (вода) вокруг понтона таким образом, чтобы:

• Слева и сверху от понтона было пространство, приблизительно равное одной длине понтона;

• Справа от понтона было пространство, приблизительно равное 3- 4 длин понтона;

• Снизу – 2 длины;

• Глубина Flow Region =6T.

Рисунок 2 -Flow Region

0 градусов

Расчеты

Первый расчет задан таким образом, что поток набегает под углом 0 градусов к оси х

Рисунок 3 - Расположение осей

Материалом Flow Region выбрана вода

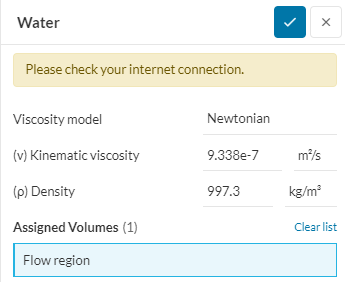
Рисунок 4 - Характеристики Flow Region

Заданы следующие начальные условия:

𝑈_𝑥 = 0,63

Граничные условия:

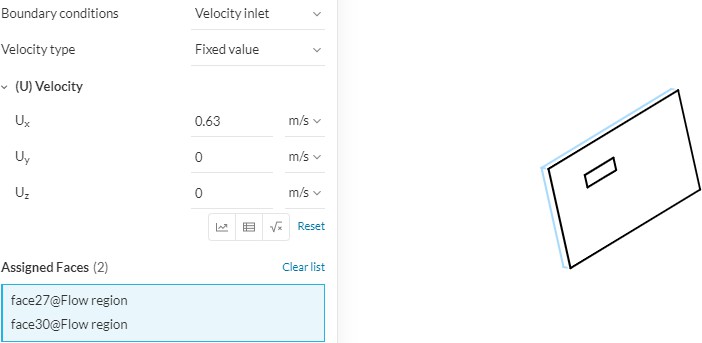
Рисунок 5 - Граничные условия (скорость)

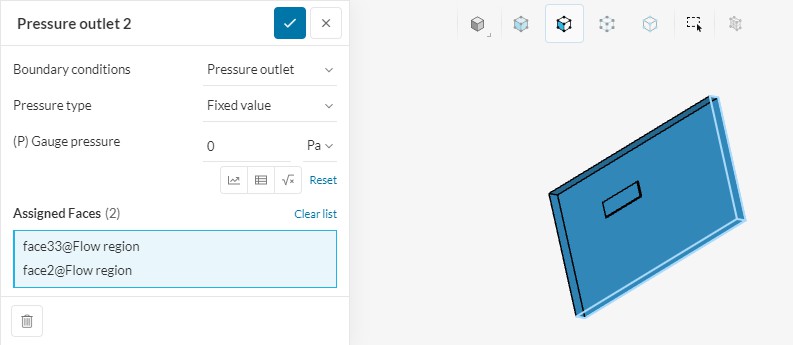
Рисунок 6 - Граничные условия (давление)

По ватерлинии была задана плоскость симметрии:

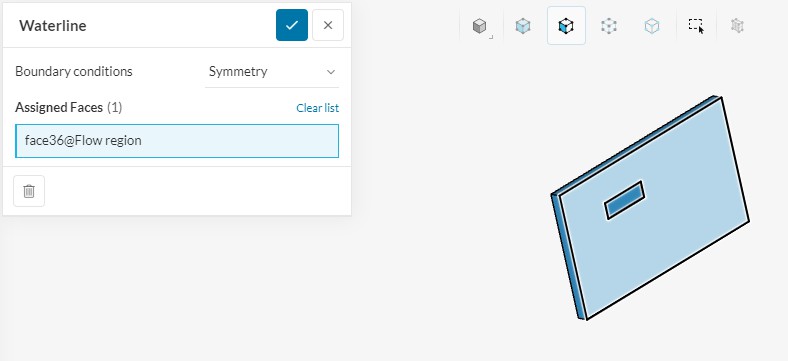
Рисунок 7 - Граничные условия (симметрия)

С помощью граничного условия «Wall => Slip» была задана имитация дна.

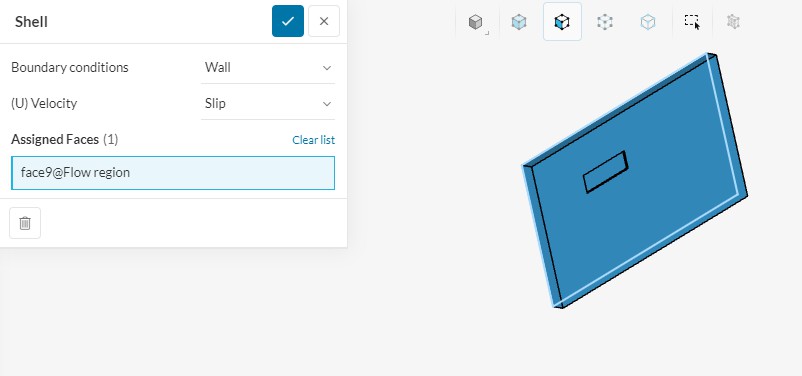
Рисунок 8 - граничные условия (стена)

Также с помощью граничного условия «Wall», но в данном случае «No-Slip» был сымитирован корпус понтона

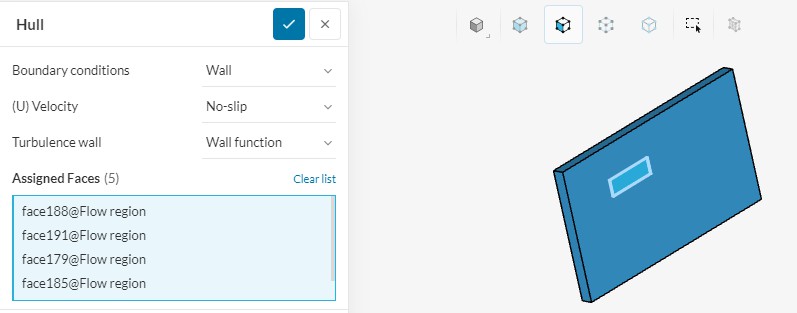
Рисунок 9 - Граничные условия (стена)

Для расчета необходимо сгенерировать сетку. А для того чтобы получить более точные значения возле корпуса понтона, должны присутствовать пограничные слои. В данном случае их три.

Рисунок 10 - Сетка и ее параметры

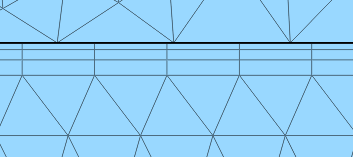
Рисунок 11 - Пограничные слои

В результате получилось следующее:

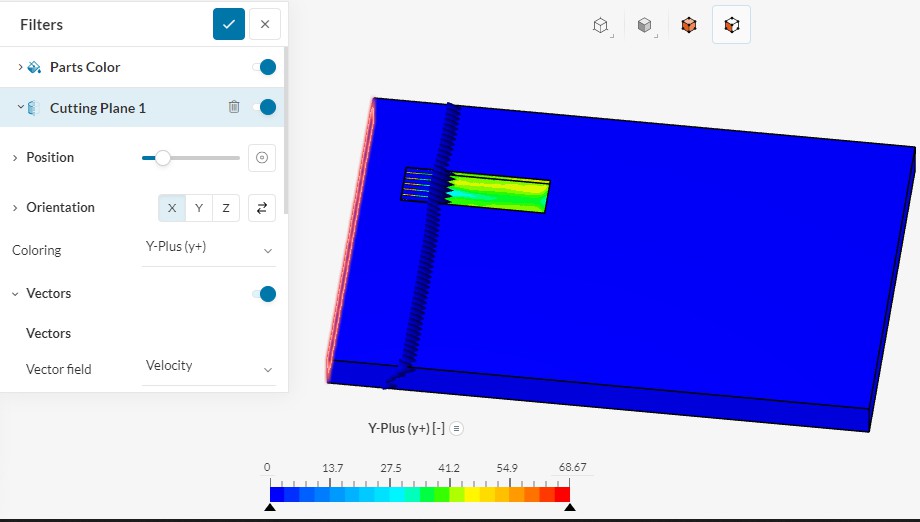
Рисунок 12 - направление векторов скорости

𝑋 = 𝑋_𝑝 + 𝑋_𝑣 = 9,67 + 0,43 = 10,1 Н

𝑌 = 𝑌_𝑝 + 𝑌_𝑣 = 0,04 − 0,02 = 0,02 Н

𝑀_𝑧 = 𝑀_𝑧𝑝 + 𝑀_𝑧𝑣 = 0,026 − 0,003 = 0,023 Нм

10 градусов

Поток набегает под углом 10 градусов к оси х

В этой и последующих симуляциях меняются только граничные условия, связанные со скоростями.

Рисунок 13 - Граничные условия (скорость; 10 градусов)

Рисунок 14 - Направление векторов скорости

𝑋 = 𝑋_𝑝 + 𝑋_𝑣 = 10,82 + 0,79 = 11,61 Н

𝑌 = 𝑌_𝑝 + 𝑌_𝑣 = −3,14 − 0,23 = −3,37 Н

𝑀_𝑧 = 𝑀_𝑧𝑝 + 𝑀_𝑧𝑣 = 0,498 − 0,026 = 0,472 Нм

20 градусов

Поток набегает под углом 20 градусов к оси х

В этой и последующих симуляциях меняются только граничные условия, связанные со скоростями.

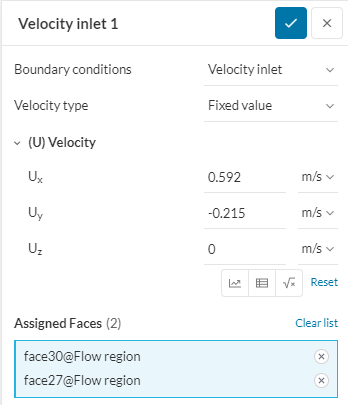
Рисунок 15 - Граничные условия (скорость; 10 градусов)

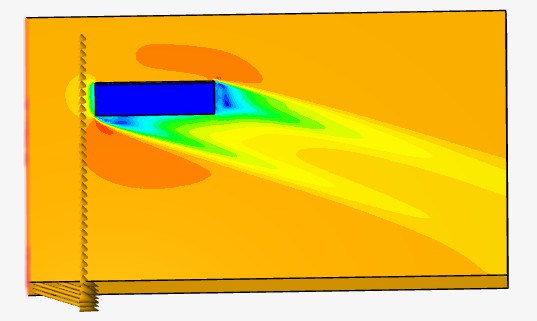
Рисунок 16 - Направление векторов скорости

𝑋 = 𝑋_𝑝 + 𝑋_𝑣 = 10,49 + 0,99 = 11,48 Н

𝑌 = 𝑌_𝑝 + 𝑌_𝑣 = −8,16 − 0,42 = −8,58 Н

𝑀_𝑧 = 𝑀_𝑧𝑝 + 𝑀_𝑧𝑣 = 1,08 + 0,01 = 1,09 Нм

30 градусов

Поток набегает под углом 30 градусов к оси х

В этой и последующих симуляциях меняются только граничные условия, связанные со скоростями.

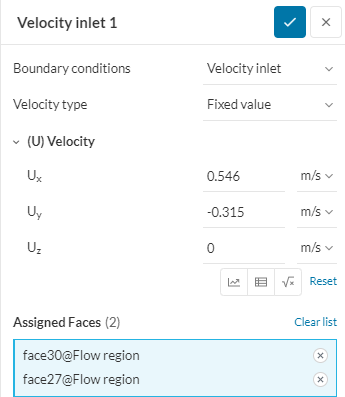
Рисунок 17 - Граничные условия (скорость; 10 градусов)

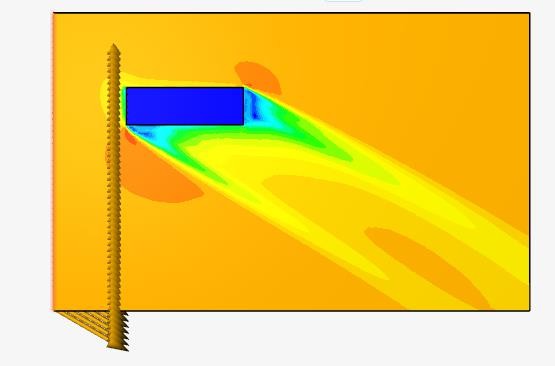
Рисунок 18 - Направление векторов скорости

𝑋 = 𝑋_𝑝 + 𝑋_𝑣 = 9,33 + 1,01 = 10,34 Н

𝑌 = 𝑌_𝑝 + 𝑌_𝑣 = −13,79 − 0,52 = −14,31 Н

𝑀_𝑧 = 𝑀_𝑧𝑝 + 𝑀_𝑧𝑣 = 1,66 + 0,06 = 1,72 Нм

45 градусов

Поток набегает под углом 45 градусов к оси х

В этой и последующих симуляциях меняются только граничные условия, связанные со скоростями.

Рисунок 19 - Граничные условия (скорость; 10 градусов)

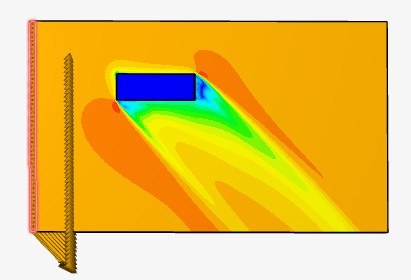
Рисунок 20 - Направление векторов скорости

𝑋 = 𝑋_𝑝 + 𝑋_𝑣 = 6,80 + 0,91 = 7,71 Н

𝑌 = 𝑌_𝑝 + 𝑌_𝑣 = −22,42 − 0,48 = −22,9 Н

𝑀_𝑧 = 𝑀_𝑧𝑝 + 𝑀_𝑧𝑣 = 2,55 + 0,13 = 2,68 Нм

90 градусов

Поток набегает под углом 90 градусов к оси х

В этой и последующих симуляциях меняются только граничные условия, связанные со скоростями.

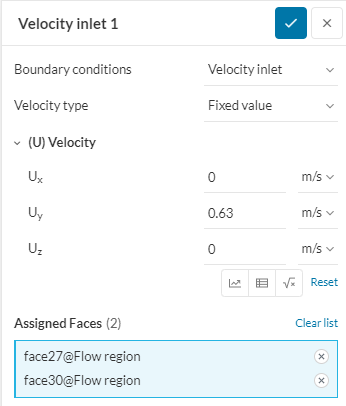
Рисунок 21 - Граничные условия (скорость; 10 градусов)

Рисунок 22 - Направление векторов скорости

𝑋 = 𝑋_𝑝 + 𝑋_𝑣 = −2,25 − 0,25 = −2,5 Н

𝑌 = 𝑌_𝑝 + 𝑌_𝑣 = 29,56 + 0,21 = 29,77 Н

𝑀_𝑧 = 𝑀_𝑧𝑝 + 𝑀_𝑧𝑣 = 2,596 + 0,105 = 2,701 Нм

Построение графиков зависимости позиционных характеристик от угла 𝜷.

Таблица 1 - Исходные данные для построения графиков

β	X	𝑪𝒙	Y	𝑪𝒚	𝑴𝒛	𝑪𝑴𝒛
0	10,1	402,98	0,02	0,80	0,023	0,49
10	11,61	463,23	-3,37	-134,46	0,472	9,99
20	11,48	458,04	-8,58	-342,33	1,09	23,07
30	10,34	412,56	-14,31	-570,96	1,72	36,41
45	7,71	307,62	-22,9	-913,69	2,68	56,73
60	4,61	183,93	-30,71	-1225,30	3,13	66,25
75	2,29	91,37	-33,13	-1321,86	2,37	50,16
90	-0,061	-2,43	-33,34	-1330,23	-0,475	-10,05

В этой таблице:

2𝑋

^{𝐶𝑥 =} 𝜌𝑣²𝐿𝑇

2𝑌

^{𝐶𝑦 =} 𝜌𝑣²𝐿𝑇

₂𝑀_𝑧

^{𝐶𝑀𝑧 =} 𝜌𝑣²𝐿²𝑇

500,00

400,00

300,00

Сх

200,00

100,00

0,00

-100,00

Название оси

Рисунок 23 - Зависимость Сх от 𝜷

200,00

0,00

-200,00

-400,00

Су

-600,00

-800,00

-1000,00

-1200,00

-1400,00

-1600,00

Название оси

Рисунок 24 - Зависимость Сy от β

80,00

70,00

60,00

50,00

CMz

40,00

30,00

20,00

10,00

0,00

-10,00

-20,00

0 20 40 60 80 100

β

Рисунок 25 - Зависимость СMz от β

Вывод

В ходе работы над курсовым проектом была сделана модель прямоугольного понтона с заданными главными размерениями. С помощью этой модели и доступными ПО были найдены позиционные характеристики (безразмерные гидродинамические коэффициенты), которые пригодятся для дальнейшего исследования гидродинамических характеристик понтона.