Примеры курсовых / 4_kursovaya_Skirdova

Национальный исследовательский ядерный университет

Московский инженерно-физический институт

Кафедра физики прочности

Курсовая работа по дисциплине

«Основы сопротивления материалов»

Задача № 4 Схема № 18 Вариант № 18

Студент __Скирдова Елена___

Группа ____Б19-204_________

Преподаватель Симонов В.Н.

Дата выполнения работы: 10.05.21

Москва – 2021

1

Таблица 4

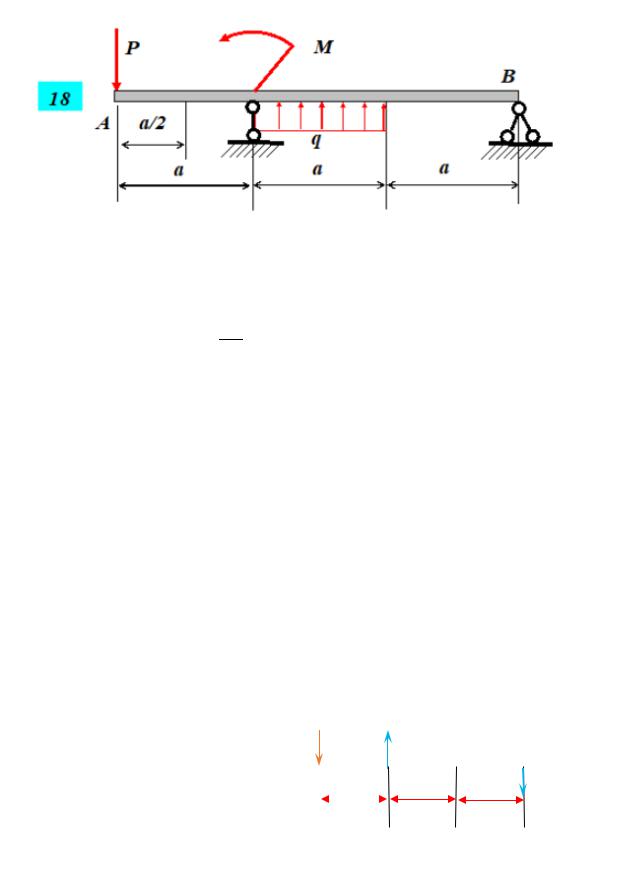
Схема

РЕШЕНИЕ

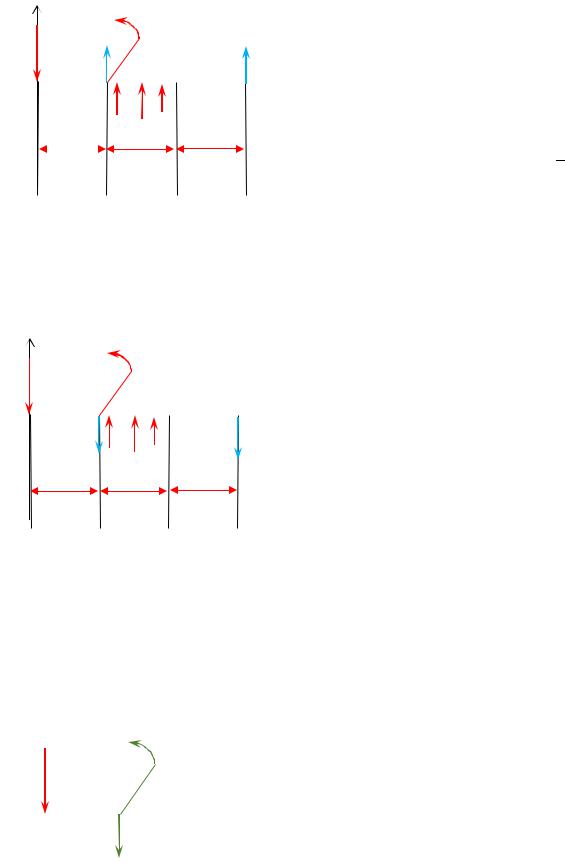
1. Определение опорных реакций.

Балка лежит на двух видах опор: шарнирно-подвижной опоре – и шарнирно-неподвижной опоре.

2

СЕЧЕНИЕ CD

4

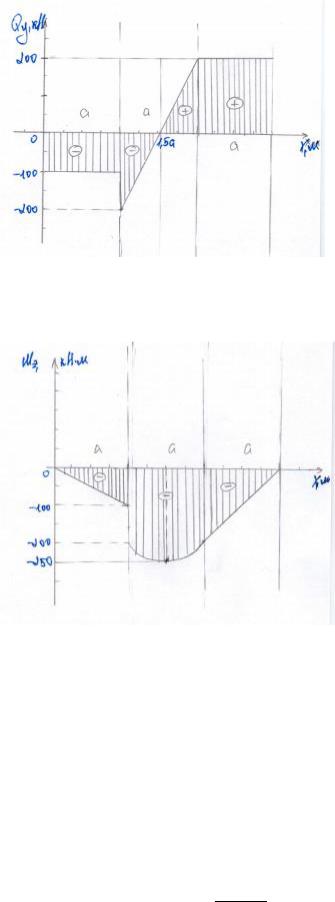
Эпюра поперечных сил Qy :

Эпюра изгибающих моментов Mz:

3.Определение размеров поперечного сечения из условия прочности

В опасном сечении должно выполняться условие прочности:

Из условия [ ] = 160 Мпа.

Из предыдущих вычислений имеем | | = 250 кН на участке ВС. Тогда

≥ | | ≥ 1562.5 10−6м3

σ

≥ 1562.5 см3

5

Определение размеров сечений:

1. Круглое сечение:

3= 32 = 1562.5 см3

2. Прямоугольное сечение:

33

= √ 2 = 0.1328 м

h = 2b = 0.2657 м

3. Двутавровое сечение:

= . см

Из ГОСТ 8238-89:

6

4. Построение эпюры нормальных σ и касательных напряжений.

Опасным сечением, является середина участка ВС, но так как | = 0,

= /2

то рассмотрим сечение С:

= 200 кН

= −200 кН м

Двутавровое сечение:

= 39727 см4

= |2

−2

| = 125.86 МПа

2

| = −125.86 МПа

−2

На уровне перехода от стенки к полке:

7

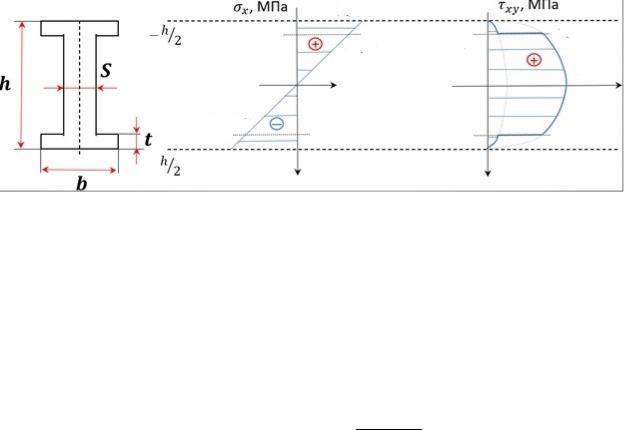
Эпюры:

125.86

−118.21

−125.86

5.Анализ напряженного состояния для двутавра в точке перехода от полки в стенку в зоне растяжения на уровне минимальной ширины.

= 200 кН > 0

В зоне растяжения: 2 =125.86 Мпа

На уровне минимальной ширины: (2) = 31.53 Мпа

Тогда главные напряжения 1, 2, 3 и :

1 = = 133.32 МПа

2 = 0

3 = = −7.46 МПа

8

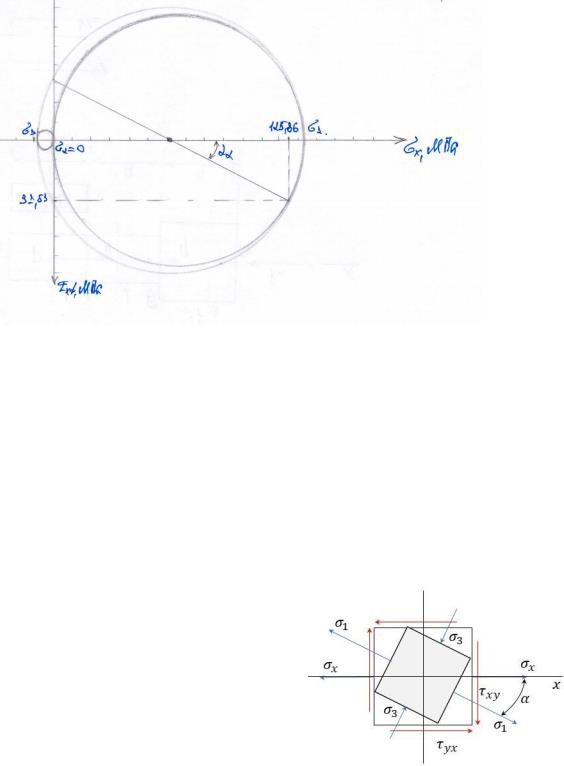
Теперь качественно оценим правильность полученных результатов с помощью кругов Мора.

Из кругов Мора получаем:

1 ≈ 133 МПа

2 = 0

3 ≈ −8 МПа

Следовательно, данные полученные аналитически и графически совпадают.

Представим результаты на элементарном кубике:

9

6.Определение линейного в точке А и углового в сечении В перемещения с помощью интеграла Мора.

Интеграл Мора имеет следующий вид:

1= ∫ 1

– обобщенное перемещение,– модуль Юнга,– освой момент инерции,– длина балки,

– эпюра изгибающего момента от всех внешних нагрузок,1 – эпюра изгибающего момента от единичной нагрузки,– продольная ось балки.

В случае определения линейного перемещения сечения обобщенное перемещение равно. Тогда в искомой точке прикладывается единичная сила P = 1Н в поперечном направлении (ось ), определяется момент в каждом участке от этой единичной силы и вычисляется интеграл Мора.

а) Определение линейного перемещения в сечении А