Практическая №3 (Построение множественной регрессии) / Практическая №3 (Вариант 13) / Практическая №3 (Вариант 13)

ГУМРФ имени адмирала С.О. Макарова

ИНСТИТУТ ВОДНОГО ТРАНСПОРТА

Кафедра технологии судоремонта

Практическая работа №3

ПОСТРОЕНИЕ МНОЖЕСТВЕННОЙ РЕГРЕССИИ

по дисциплине «Теория инженерного эксперимента»

Вариант №13

Выполнил студент группы М-11 Чернов Н.Е.

Проверил преподаватель к.т.н. Горбаченко Е.О.

Санкт-Петербург

2024

Цель работы: получение умений и навыков в обработке результатов экспериментов методом наименьших квадратов

Номер опыта	Значение факторов		Результат опыта (y)		Примечание
			1-я попытка	2-я попытка (повтор)
1	15	67	165	155	- межэлектродное расстояние (мм); - расстояние от верх. торца вертикально располо женной втулки (мм); y – толщина хромового покрытия (мкм).
2	30	67	135	125
3	15	317	228	232
4	30	317	200	210

Найдём среднее значение отклика по результатам двух попыток проведения опыта:

, при ;

, при ;

, при ;

, при .

Запишем систему уравнений для модели, представленной в виде гиперболоида:

;

;

;

.

;

;

;

.

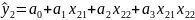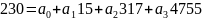Произведём замену переменных: 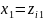; ; , тогда запишем уравнения следующим образом:

;

;

;

.

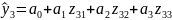Решение этой системы в матричном виде записывается в виде уравнения:

Где А – вектор-столбец искомых параметров:

1
1
1
1

Z – матрица всех значений факторов, использованных при проведении опытов:

1	15	67	1005
1	30	67	2010
1	15	317	4755
1	30	317	9510

Z = =

– матрица, транспонированная по отношению к матрице Z,

Y – вектор-столбец опытных значений изучаемой величины y:

160

130

230

205

Y = =

1	1	1	1
15	30	15	30
67	67	317	317
1005	2010	4755	9510

Z^T=

725

15900

157325

3465300

Найдем произведение матриц Z^TY =

Найдем аналогично произведение матриц:

4	90	768	17280
90	2250	17280	432000
768	17280	209956	4724010
17280	432000	4724010	118100250

Z^TZ =

Находим обратную матрицу:

2,54	-0,085	-0,008	0,0007
-1,268	0,085	0,004	-0,0007
-0,536	0,018	0,008	-0,0007
0,268	-0,018	-0,004	0,0007

(Z^TZ)^-1 =

Наконец, перемножаем матрицы и получаем искомое A: А = (Z^TZ)^-1 на Z^TY:

1657

-1366

-1265

1705

А =

Значит, искомая модель будет иметь следующий вид:

Рисунок 1 – Графическое изображение функции отклика