1. Энергия и импульс

Энергией покоя 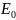материальная точка обладает в ИСО относительно которой она покоится и называется собственной энергией материальной точки:

где — масса покоя материальной точки, кг; с — скорость света, .

Любое изменение энергии материальной точки означает изменение её массы и наоборот:

где 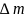— изменение массы материальной точки, кг; с — скорость света, .

Полная энергия материальной точки:

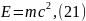
где 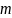— масса материальной точки, кг; с — скорость света, .

Между полной энергией материальной точки, энергией покоя и импульсом существует зависимость:

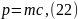
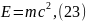
значит:

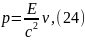
составим:

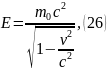
запишем:

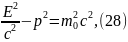
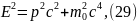
тогда:

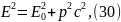
где — энергия покоя, Дж; p — импульс, кг. — скорость света, ; m — масса материальной точки, кг; Е — полная энергия, Дж; — масса покоя, кг; inv — инвариант.

3. Длина тел в различных системах отсчета

Рассмотрим стержень, расположенный вдоль оси   и покоящийся в системе отсчёта К'. Длина стержня в системе К' будет 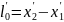 , где  ,   – не изменяющиеся со временем t' координаты начала и конца стержня., а индекс 0 показывает, что в системе К' стержень покоится. Теперь определим длину этого стержня в системе К, относительно которой он движется, со скоростью 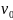 . Для этого измерим координаты концов стержня  и    системе К в один и тот же момент времени t. Их разность  и определяет длину стержня в системе К. Используя преобразования Лоренца получим:

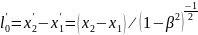  _, (31)

или

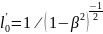(32)

Таким образом, длина стержня, измеренная в системе, относительно которой он движется, оказывается меньше длины, измеренной в системе отсчёта, относительно которой стержень покоится.

Из формулы (32) следует, что линейный размер тела, движущегося относительно инерциальной системы отсчёта, уменьшается в направлении движения в 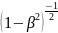  раз, то есть так называемое лоренцево сокращение длины тем больше, чем больше скорость движения.

Из преобразований Лоренца следует: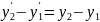 ;  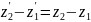,то есть поперечные размеры тела не зависят от скорости его движения и одинаковы во всех инерциальных системах отсчёта.

Таким образом, линейные размеры тела наибольшие в той системе отсчёта, относительно которой тело покоится.

3.1. Длительность событий в различных системах отсчёта.

Пусть в некоторой точке (с координатой x), покоящейся относительно системы К, происходит событие, длительность которого (разность показаний часов в начале и конце события) τ = t₂ - t₁, где t₁ – начало события, а t₂ – конец события. В системе К` длительность события - t’,

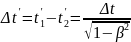(33)

То есть

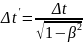(34)

Длительность события, происходящего в некоторой точке ИСО, наименьшая в той ИСО, относительно которой точка неподвижна. Время, отсчитанное по часам, движущимся вместе с телом, называется собственным, оно обозначается t’ = τ₀.

Промежуток времени

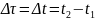(35)

это промежуток времени между теми же событиями, измеренный по часам системы К, относительно которой частица (вместе со своими часами) движется со скоростью  . Если поместим в систему К наблюдателя, то с его точки зрения t – промежуток времени, измеренный по неподвижным часам, а t₀ – по часам, движущимся со скоростью V₀ и, τ < t.

Вывод: движущиеся часы идут медленнее покоящихся.

Выводы

В работе были рассмотрены основные понятия в специальной теории относительности. Из представленного выше материала можно сделать выводы.

1.Законы классической ньютоновской механики могут применяться только при скоростях много меньших скорости света. Это даёт нам понимание об малом количестве обстоятельств, при которых можно будет описать движение тела классическими ньютоновскими законами.

2.Преобразования Лоренца не отрицают преобразованию Галилея, а только дополняют их. Они считаются верными при любых скоростях, а классическая механика верна лишь в частных случаях.

3.Классическая механика является частным случаем релятивистской механики и при скоростях малы по отношению к скорости света скоростью света.

Литература

1. Угаров, В.А. Специальная теория относительности / В.А. Угаров. – 2-е изд. – Москва: Издательство «Наука» Главная редакция физико-математической литературы, 1977. – 384 с.

2. Яворский, Б.М. Справочник по физике / Б.М. Яворский, А.А. Детлаф. – 3-е изд. – Москва: Издательство «Наука» Главная редакция физико-математической литературы, 1990. – 624 с.