
БЕЛОРУССКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ АВИАЦИИ
Факультет гражданской авиации
Кафедра естественнонаучных и общепрофессиональных дисциплин
ОТЧЕТ
по самостоятельной работе по теме
«ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ. ОСНОВНЫЕ ПОНЯТИЯ И ПОСТУЛАТЫ»
по дисциплине физика
СОДЕРЖАНИЕ
Введение……………………………………………………………………………...31. Преобразования Лоренца и следствия из них…………………………………...5
2. Законы сохранения в релятивисткой механике………………………………..12
3. Длина тел в различных системах отсчета……………………………………...17
Выводы……………………………………………………………………………...19
Литература………………………………………………………………………......20
Введение
Принцип относительности – фундаментальный физический закон, согласно которому любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя, и в такой же системе в состоянии равномерного прямолинейного движения. Состояния движения или покоя определяются по отношению к произвольно выбранной инерциальной системе отсчета. Принцип относительности лежит в основе специальной теории относительности Эйнштейна.
Инерциальная система отсчета (ИСО) – понятие классической механики, первой фундаментальной физической теории, которая имеет высокий статус и в современной физике. Основы этой теории заложил И.Ньютон.
«Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние» – так Ньютон сформулировал закон, который сейчас называется первым законом механики Ньютона, или законом инерции.
Система отсчета, в которой справедлив закон инерции: материальная точка, когда на нее не действуют никакие силы (или действуют силы взаимно уравновешенные), находится в состоянии покоя или равномерного прямолинейного движения, – называется инерциальной. Всякая система отсчета, движущаяся по отношению к ней поступательно, равномерно и прямолинейно, есть также инерциальная.
Теория относительности – физическая теория пространства и времени. В частной (специальной) теории относительности рассматриваются только инерциальные системы отсчета. Явления, описываемые теорией относительности, называются релятивистскими (от лат. «относительный») и проявляются при скоростях, близких к скорости света в вакууме (эти скорости тоже принято называть релятивистскими).
Существует фактически две различных теории относительности, известных в физике, одна из них называется специальной (частной) теорией относительности, другая – общей теорией относительности. Альберт Эйнштейн предложил первую из них в 1905 г., вторую – в 1916 г. Принимая во внимание, что специальная теория относительности связана, в первую очередь, с электрическими и магнитными явлениями и с их распространением в пространстве и времени, общая теория относительности была разработана, прежде всего, чтобы иметь дело с тяготением. Обе теории сосредотачиваются на новых подходах к пространству и времени, подходах, которые отличаются глубоко от тех, которые используются в каждодневной жизни; но релятивистские понятия пространства и времени неразрывно вплетаются в любую современную интерпретацию физических явлений в пределах от атома до вселенной в целом.
Преобразования Лоренца и следствия из них
Рассмотрим некоторые следствия преобразований Лоренца, выявляющие то новое, что они вносят в представления о пространстве и времени.
 Предельный
случай медленных движений
Предельный
случай медленных движений
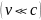 В
механике макроскопических тел, имеющей
дело со скоростями, гораздо
меньшими скорости света,
хорошо подтверждается принцип
относительности, основанный на
преобразованиях Галилея. Поэтому в
пределе медленных
движений преобразования Лоренца должны
сводиться к преобразованиям Галилея.
Однако если считать
В
механике макроскопических тел, имеющей
дело со скоростями, гораздо
меньшими скорости света,
хорошо подтверждается принцип
относительности, основанный на
преобразованиях Галилея. Поэтому в
пределе медленных
движений преобразования Лоренца должны
сводиться к преобразованиям Галилея.
Однако если считать
 0, то преобразования принимают вид
0, то преобразования принимают вид
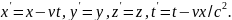 (1)
(1)
Как
видно, они отличаются от преобразований
Галилея тем, что вместо абсолютного
времени
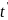 = t
вводится местное время Лоренца
= t
вводится местное время Лоренца
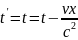 Однако
для реальных физических задач
пространственные координаты можно
считать ограниченными. Поэтому, исключая
бесконечно удаленные точки, т. е.
полагая
Однако
для реальных физических задач
пространственные координаты можно
считать ограниченными. Поэтому, исключая
бесконечно удаленные точки, т. е.
полагая 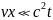 убеждаемся,
что преобразования в самом деле переходят
в преобразования Галилея.
убеждаемся,
что преобразования в самом деле переходят
в преобразования Галилея.
Таким образом, новая теория пространства-времени, основанная на преобразованиях Лоренца, удовлетворяет принципу соответствия, переходя в пределе медленных движений в старую теорию Ньютона-Галилея. Выполнение принципа соответствия является необходимым условием, предъявляемым ко всякой новой теории, поскольку старая, хорошо проверенная теория обязательно должна содержаться в новой в качестве предельного случая, то есть при изменении входящих в теорию параметров в некоторой ограниченной области.
Преобразования Лоренца теряют
физический смысл при
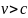 В
самом деле, в этом случае
В
самом деле, в этом случае
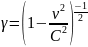 становится
мнимой величиной, а вместе с ней мнимыми
оказываются и новые координаты
становится
мнимой величиной, а вместе с ней мнимыми
оказываются и новые координаты
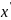 и время
.
Но результаты любых измерений пространства
и времени выражаются в действительных числах,
поэтому физический смысл имеют лишь
действительные координаты и время.
Следовательно, системы отсчета, движущиеся
со скоростью, превышающей скорость света в
вакууме, не имеют физического смысла и
должны быть изъяты из рассмотрения.
Вместе с тем преобразования, осуществляющие
переход к таким системам и рассматриваемые
формально математически, безусловно
могут оказаться полезными при решении
некоторых задач.
и время
.
Но результаты любых измерений пространства
и времени выражаются в действительных числах,
поэтому физический смысл имеют лишь
действительные координаты и время.
Следовательно, системы отсчета, движущиеся
со скоростью, превышающей скорость света в
вакууме, не имеют физического смысла и
должны быть изъяты из рассмотрения.
Вместе с тем преобразования, осуществляющие
переход к таким системам и рассматриваемые
формально математически, безусловно
могут оказаться полезными при решении
некоторых задач.
Ранее,
анализируя распространение световой волны в
двух инерциальных системах отсчета
 и
и
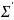 ,
находящихся в относительном движении,
мы пришли к выводу, что постулаты
Эйнштейна непротиворечивы только при
допущении относительности одновременности
пространственно-разобщенных событий.
Убедимся теперь в этом с помощью
преобразований Лоренца. При этом для
упрощения картины вообще не будем
рассматривать координаты y
и z
,
находящихся в относительном движении,
мы пришли к выводу, что постулаты
Эйнштейна непротиворечивы только при
допущении относительности одновременности
пространственно-разобщенных событий.
Убедимся теперь в этом с помощью
преобразований Лоренца. При этом для
упрощения картины вообще не будем
рассматривать координаты y
и z
Пусть
в неподвижной системе отсчета
зафиксированы
два пространственно-разобщенных события
(t1
, x1)
и (t2,
x2),
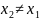 посмотрим,
как будут выглядеть эти события в системе
, движущейся
со скоростью
посмотрим,
как будут выглядеть эти события в системе
, движущейся
со скоростью
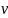 .
Применяя преобразования Лоренца,
имеем
.
Применяя преобразования Лоренца,
имеем
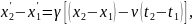
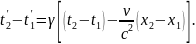 (2)
(2)
Допустим, что в системе события одновременны, то есть
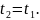
Тогда в системе , справедливы соотношения
 (3)
(3)
откуда
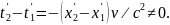 (4)
(4)
Таким образом, события, одновременные в системе , становятся неодновременными в системе , то есть одновременность пространственно разобщенных событий относительна. Это обстоятельство является тем существенно новым, что вносится преобразованиями Лоренца в наши представления о пространстве-времени.
В
самом деле, в классической механике Ньютона,
основанной на принципе относительности
Галилея, время считалось абсолютным и
признавалась лишь пространственная
относительность, то есть относительность
одноместности событий, разделенных во
времени. Так, если в системе
события (t1
, x1)
и (t2,
x2), происходят
в одной точке (x1
= x2) и
в разные моменты времени
 ) то
в системе
согласно преобразованиям Галилея,
они будут разделены отрезком
) то
в системе
согласно преобразованиям Галилея,
они будут разделены отрезком
 . Что
же касается одновременности событий,
то она считалась абсолютной:
. Что
же касается одновременности событий,
то она считалась абсолютной:
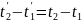 .
.
Чтобы нагляднее представить себе относительность одновременности, рассмотрим ее проявление на конкретной модели. Допустим, что в системе одновременно вспыхнули расставленные вдоль оси лампочки. Тогда в системе вспышки не будут одновременными и лампочки зажигаются последовательно одна за другой, причем фронт вспышек, перемещается со скоростью
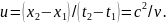 (5)
(5)
Эта скорость связана с относительной скоростью систем и соотношением
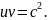
Использованным
в свое время Луи де Бройлем для описания
«волн материи». Де Бройль предположил,
что со всякой неподвижной частицей
массы 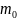 связан
некоторый периодический процесс
частоты
связан
некоторый периодический процесс
частоты 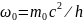 ,
где
,
где
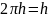 -
постоянная Планка. Иначе говоря, он
постулировал существование волнового
поля
-
постоянная Планка. Иначе говоря, он
постулировал существование волнового
поля
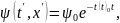 (6)
(6)
Изменяющегося по гармоническому закону одновременно во всех точках пространства. Если же частица движется со скоростью
![]() (7)
(7)
То,
считая поле
 скалярным,
найдем, что в системе
связанной с частицей, поле де Бройля
имеет вид
скалярным,
найдем, что в системе
связанной с частицей, поле де Бройля
имеет вид
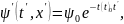 (8)
(8)
А в системе , согласно преобразованиям Лоренца,
 ,
(9)
,
(9)
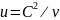 ,
,
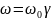 ,
,
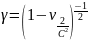 .
.
Таким
образом, с каждой движущейся со скоростью
частицей
связано поле де Бройля в виде плоской
волны, распространяющейся в пространстве
с фазовой скоростью 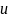 определяемой
соотношением.
определяемой
соотношением.
Ограниченность
скорости распространения сигнала. Формулы
позволяют также сделать вывод о том,
что скорость любого сигнала, то есть
возмущения, переносящего информацию,
не может превышать скорость света с.
В самом деле, пусть сигнал, посылаемый
из точки X1 в
момент времени t1 принимается
в точке X2 в
момент времени t2.
Очевидно, что момент испускания сигнала
предшествует моменту его приема, то
есть 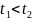 а
скорость распространения сигнала равна
а
скорость распространения сигнала равна
 (10)
(10)
В то же время в движущейся системе отсчета
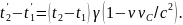 (11)
(11)
Так
как для всех реальных систем отсчета 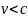 ,то
при
,то
при  всегда
всегда
 и
поэтому из
и
поэтому из 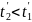 то
есть последовательность моментов
испускания сигнала и его приема
сохраняется неизменной во всех
реальных инерциальных системах
отсчета.
то
есть последовательность моментов
испускания сигнала и его приема
сохраняется неизменной во всех
реальных инерциальных системах
отсчета.
Однако
если 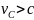 ,
то найдутся системы отсчета, удовлетворяющие
условию
,
то найдутся системы отсчета, удовлетворяющие
условию
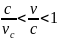 ,
,
Для
которых
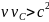 поэтому
. Но
такое изменение последовательности
моментов испускания и поглощения сигнала
в зависимости от выбора системы отсчета
(всегда произвольного) несовместимо с
принципом причинности, по крайней мере
в той форме, в какой он выполняется для
всех макроскопических процессов.
Согласно этому принципу, всякая информация
сначала посылается (причина), а затем
принимается (следствие), менять причины
и следствия местами невозможно.
поэтому
. Но
такое изменение последовательности
моментов испускания и поглощения сигнала
в зависимости от выбора системы отсчета
(всегда произвольного) несовместимо с
принципом причинности, по крайней мере
в той форме, в какой он выполняется для
всех макроскопических процессов.
Согласно этому принципу, всякая информация
сначала посылается (причина), а затем
принимается (следствие), менять причины
и следствия местами невозможно.
Итак,
принимая принцип причинности, мы
вынуждены признать, что скорость передачи
информации не может превышать скорость света с.
Однако этот вывод не следует переносить
на все без исключения физические
процессы, поскольку не все процессы
можно превратить в сигналы, то есть
использовать для передачи информации.
Примером таких процессов могут быть,
скажем, волны де Бройля, распространяющиеся
с фазовой скоростью, превышающей скорость света.
Это связано с тем, что бесконечная
монохроматическая волна не несет никакой
информации и поэтому не может быть
сигналом. Передать информацию можно
лишь с помощью группы волн, центр которой
распространяется с групповой скоростью.
В частности, для волн де Бройля, как
можно показать, групповая скорость совпадает
со скоростью частицы, ассоциируемой с
этой волной, и связана с фазовой скоростью
и волны соотношением. При этом 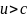 ,
так как
и
предполагается, что с частицей всегда
можно связать систему отсчета.
,
так как
и
предполагается, что с частицей всегда
можно связать систему отсчета.
Допустимо
существование и реальных частиц,
движущихся со скоростью, большей скорости света,
если отказаться от обычно подразумеваемой
независимости процессов их испускания
и поглощения. Для обычных, досветовых,
частиц 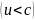 процесс
испускания (эмиссии) во всех возможных
системах отсчета предшествует процессу
поглощения (абсорбции). Для сверхсветовых
же частиц
процесс
испускания (эмиссии) во всех возможных
системах отсчета предшествует процессу
поглощения (абсорбции). Для сверхсветовых
же частиц 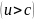 последовательность
процессов эмиссии и абсорбции зависит
от выбора системы отсчета, то есть
произвольна. Таким образом, если
допустить, что сверхсветовая частица,
испущенная в точке X1 эмиттером E, поглощается
в точке X2 регистрирующим
прибором—абсорбером А, то в некоторой
другой возможной системе отсчета процесс
абсорбции в точке
последовательность
процессов эмиссии и абсорбции зависит
от выбора системы отсчета, то есть
произвольна. Таким образом, если
допустить, что сверхсветовая частица,
испущенная в точке X1 эмиттером E, поглощается
в точке X2 регистрирующим
прибором—абсорбером А, то в некоторой
другой возможной системе отсчета процесс
абсорбции в точке 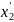 предшествует
процессу эмиссии в точке
предшествует
процессу эмиссии в точке
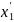 . Тем
самым нарушается макроскопическая
причинность, гак как следствие (регистрация
частицы) предшествует причине (испусканию
частицы). Если же для сверхсветовых
частиц не противопоставлять процессы
поглощения и испускания, а рассматривать
их как единый процесс эмиссии—абсорбции,
или абсорбции — эмиссии, то есть не
считать возможной регистрацию лишь
одного процесса поглощения частицы, а
полагать осуществимой только регистрацию
всего процесса сразу в обеих точках X1
и X2, то
противоречия с принципом причинности
не возникнет.
. Тем
самым нарушается макроскопическая
причинность, гак как следствие (регистрация
частицы) предшествует причине (испусканию
частицы). Если же для сверхсветовых
частиц не противопоставлять процессы
поглощения и испускания, а рассматривать
их как единый процесс эмиссии—абсорбции,
или абсорбции — эмиссии, то есть не
считать возможной регистрацию лишь
одного процесса поглощения частицы, а
полагать осуществимой только регистрацию
всего процесса сразу в обеих точках X1
и X2, то
противоречия с принципом причинности
не возникнет.
Таким образом, теории относительности не противоречит допущение о существовании точечных объектов, движущихся со сверхсветовой скоростью, испускаемых и поглощаемых обычными частицами в различных пространственных точках. Однако последовательность процессов эмиссии и абсорбции для этих объектов относительна, то есть зависит от выбора системы отсчета. Такие гипотетические сверхсветовые частицы (тахионы) представляются в одной системе отсчета движущимися от точки X1 к точке X2 а в другой – от X2 к X1.
Помимо эффекта десинхронизации имеется еще два кинематических эффекта теории относительности (уже второго порядка), наиболее поражающие воображение: это эффекты сокращения движущихся масштабов и замедления хода движущихся часов.
