СОДЕРЖАНИЕ

1 КОРНЕВЫЕ КРИТЕРИИ КАЧЕСТВА ПЕРЕХОДНЫХ ПРОЦЕССОВ 2

2 ВЫПОЛНЕНИЕ ЛАБОРАТОРНОЙ РАБОТЫ 7

3 ИССЛЕДОВАНИЕ ВЛИЯНИЯ НУЛЕЙ И ПОЛЮСОВ 11

3.1 ВАРИАНТ 1 11

3.2 ВАРИАНТ 2 16

3.3 ВАРИАНТ 3 20

3.4 ВАРИАНТ 4 24

ЗАКЛЮЧЕНИЕ 28

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 29

111Equation Chapter 1 Section 1исследование влияния нулей и полюсов

Цель работы: исследование влияния взаимного расположения нулей и полюсов передаточной функции разомкнутой системы на динамические свойства замкнутой системы.

1 Корневые критерии качества переходных процессов

Для определения характера переходного процесса в системе используется ее реакция на единичный ступенчатый входной сигнал. Переходную характеристику h(t) системы можно вычислить с помощью обратного преобразования Лапласа, используя формулы разложения Хевисайда:

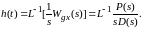
Если D(s) не имеет кратных корней, то

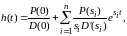(1.1)

где s_i — корни характеристического полинома замкнутой системы D(s)=0; D’(s_i)=dD(s)/ds=s_i – первая производная характеристического полинома D(s) по s при s=s_i.

Из (1) видно, что на характер переходного процесса влияют и числитель и знаменатель передаточной функции замкнутой системы  . Если числитель   не имеет нулей, то есть представляет собой постоянную величину, то характер переходных процессов можно оценить по ее полюсам, то есть корням характеристического уравнения замкнутой САУ D(s)=0.

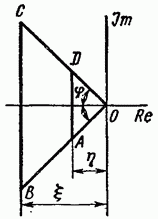
Рисунок 1.1 – Область расположения корней

На плоскости корней s можно выделить область, в которой располагаются корни характеристического уравнения системы для оценки качества ее переходного процесса. Обычно это представлено трапецией ABCD на рисунке 1.1, где корни располагаются внутри трапеции на сторонах и основаниях, а вне ее - ни одного корня. Параметры степени устойчивости η, колебательности μ и вещественной части ε максимально удаленного корня от мнимой оси определяются для выделения этой области на плоскости корней. Степень устойчивости η отражает ближайшее расстояние от мнимой оси до любого корня, определяющее основание трапеции AD на рисунке 1.1. Колебательность μ для системы характеризует количество колебаний в переходном процессе и зависит от расположения комплексно-сопряженных корней внутри трапеции ABCD. Вещественная часть ε максимально удаленного корня от мнимой оси также влияет на оценку качества переходного процесса. Она должна быть минимальной для достижения оптимальной производительности и качества работы системы.

Пусть общее решение дифференциального уравнения системы

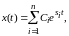(1.2)

где 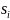  — корни характеристического уравнения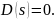 

Составляющая этого решения, определяемая степенью устойчивости, запишется в виде

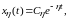(1.3)

для случая вещественных корней или

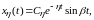(1.4)

для случая, когда среди корней есть пара комплексно-сопряженных.

Переходный процесс в системе считается закончившимся, когда затухает его медленнейшая составляющая, определяемая степенью устойчивости. Время затухания процесса можно грубо оценить по затухающей составляющей .

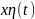Для анализа степени устойчивости системы можно определить ее коэффициенты 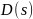и вычислить соответствующую степень устойчивости. Для синтеза системы по заданной степени устойчивости можно определить варьируемые параметры системы.

Путем смещения мнимой оси влево на величину 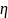можно сделать один из корней характеристического полинома системы расположенным на мнимой оси, что соответствует границе устойчивости системы. Это соответствует условию, когда старший определитель Гурвица равен нулю: 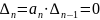. Это условие может быть использовано для определения степени устойчивости системы по ее коэффициентам или для решения обратной задачи.

Пусть характеристическое уравнение системы

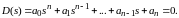
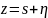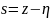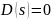Введем новую переменную  . Подставив значение   в уравнение  , получим новое смещенное уравнение:

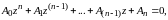2\* MERGEFORMAT (1.5)

Если в смещенном уравнении окажется 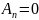 , то ближайшим к мнимой оси окажется нулевой корень, а если 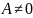 , то пара сопряженных комплексных корней.

Условие границы устойчивости для системы, описанной уравнением (1.5), по критерию Гурвица 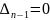  при соблюдении всех остальных условий устойчивости Гурвица.

Колебательностью системы называют тангенс угла, образованного отрицательной вещественной полуосью и лучом из начала координат к корню, у которого отношение мнимой части к действительной максимально (рисунок 1.1):

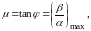3\* MERGEFORMAT (1.6)

где 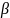– значение мнимой части корней  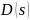;  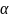– действительная часть.

При определенных параметрах системы можно рассчитать значение колебательности  (задача анализа колебательности) или решить обратную задачу и синтезировать систему с заданной колебательностью. Для этого в характеристическое уравнение системы вводится замена 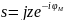, равноценная повороту мнимой оси на угол 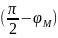 . Это приводит к тому, что пара комплексно-сопряженных корней характеристического полинома располагается на мнимой оси, а фиктивная система находится на границе устойчивости. 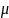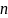Колебательность является верхней границей для оценки числа колебаний в переходном процессе. Увеличение значения приводит к увеличению числа колебаний за время регулирования.

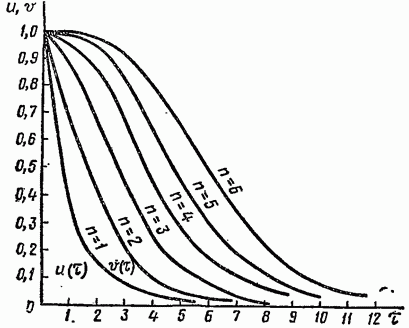
Рисунок 1.2 – Графики переходных процессов

Реальный переходный процесс может иметь значительно лучшее качество.

Запишем смещенное характеристическое уравнение:

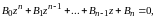4\* MERGEFORMAT (1.7)

где

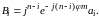5\* MERGEFORMAT (1.8)

В (1.7) часть коэффициентов — комплексные числа.

Так как фиктивная система находится на границе устойчивости, то (1.7) имеет пару сопряженных мнимых корней  .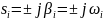

Если в (1.7) подставить 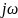  вместо  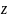и разделить смещенный характеристический полином на мнимую и действительную части, то их можно поочередно приравнять нулю, получив при этом систему двух уравнений

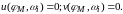
Исключив из этой системы 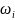получим искомое значение  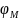и .

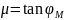Эту задачу можно решать, используя свойства корней алгебраических уравнений по формулам Виета.

Для определенных классов распределения корней и начальных условий можно построить две кривые: мажоранту и миноранту, которые ограничивают кривую переходного процесса сверху и снизу:

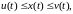6\* MERGEFORMAT (1.9)

где   — миноранта, а 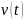  — мажоранта.

Приведем некоторые формулы для расчета мажорант и минорант без доказательства. Для случая вещественных корней и нулевых начальных условий 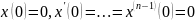  мажоранта и миноранта описываются соответственно уравнениями

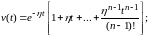7\* MERGEFORMAT (1.10)

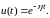8\* MERGEFORMAT (1.11)

Перерегулирование для этого класса корней отсутствует. На рисунке 1.2 показаны кривые 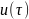и 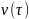для разных степеней уравнения, причем  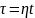 — относительное время. Чем выше  , тем грубее оценка. Если учесть величину 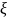 , то можно сблизить миноранту и мажоранту.

Для систем, имеющих среди корней пару комплексно-сопряженных, при тех же начальных условиях мажоранта описывается уравнением (1.10), а миноранта

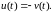9\* MERGEFORMAT (1.12)

При этом перерегулирование

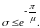10\* MERGEFORMAT (1.13)

Если  , то 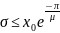  ,что проиллюстрировано на рисунке 1.3.

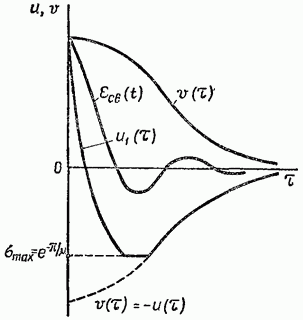
Рисунок 1.3 – График изменения переходных процессов

Используя мажоранту и миноранту, можно оценить время регулирования переходного процесса:

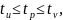
гд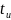е   — время регулирования по миноранте;  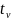— время регулирования по мажоранте.