Практическая №2 (Линейный парный регрессионный анализ) / Практическая №2 (Вариант 8) / Практическая 2

Федеральное агентство морского и речного транспорта Федеральное государственное бюджетное образовательное учреждение высшего образования ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ МОРСКОГО И РЕЧНОГО ФЛОТА имени адмирала С. О. МАКАРОВА

ИНСТИТУТ ВОДНОГО ТРАНСПОРТА

Кафедра технологии судоремонта

Журнал практических работ

по дисциплине «Теория инженерного эксперимента»

Вариант №8

Выполнил студент группы М-11 Петров К.Э.

Проверил преподаватель к.т.н Горбаченко Е.О.

Санкт-Петербург

2024 г.

Практическая работа №2

ЛИНЕЙНЫЙ ПАРНЫЙ РЕГРЕССИОННЫЙ АНАЛИЗ.

Цель работы: получение умений и навыков в обработке результатов экспериментов методом наименьших квадратов.

1. РЕШЕНИЕ ЗАДАЧИ РАСЧЀТА ПАРАМЕТРОВ АППРОКСИМИРУЮЩЕЙ ФУНКЦИИ. РЕГРЕССИОННЫЙ АНАЛИЗ. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ (МНК)

Необходимо установить вид аппроксимирующей функции графоаналитическим методом и МНК по результатам исследования времени рекристаллизации при увеличении температуры. Результаты эксперимента приведены в таблице 2. Исходные данные для оценки результатов многократных измерений представлены в таблице 1.

Таблица 1 - Исходные данные для оценки результатов многократных измерений

№ опытов (измерений)	x - абсолютная температура, К	у - время рекристаллизации, с
1	333	8000
2	340	6500
3	350	2500
4	360	1000
5	370	600
6	380	250
7	390	100
8	400	70

а) б)

Рисунок 1 – Зависимость времени рекристаллизации от увеличении температуры построенная в координатах с обычными (а) и логарифмическими (б) шкалами.

Это значит, что аппроксимирующая функция является степенной вида 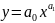. Проведём осевую линию с помощью Exele. Определим параметры и по формулам;

Постоянную определим по формуле:

Значит, по результатам графоаналитического анализа аналитический вид аппроксимирующей функции будет выглядеть следующим образом:

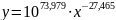
Теперь найдём вид аппроксимирующей функции с применением МНК.

Так как аппроксимирующая функция имеет вид , т. е. является степенной, произведём замену переменных: . При этом степенная функция преобразуется в линейную: .

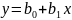Найдём параметры и 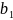новой (линейной) функции, предварительно рассчитав суммы, стоящие в этих выражениях, в табличной форме (табл. 2).

Таблица 2 - Табличная форма обработки экспериментальных данных

№ опыта
1	2,522	3,903	6,363	15,234	9,845	6,426	41,287
2	2,531	3,813	6,408	14,538	9,652	6,344	40,251
3	2,544	3,398	6,472	11,546	8,645	5,942	35,307
4	2,556	3,000	6,535	9,000	7,669	5,556	30,872
5	2,568	2,778	6,596	7,718	7,135	5,346	28,583
6	2,580	2,398	6,655	5,750	6,186	4,978	24,778
7	2,591	2,000	6,714	4,000	5,182	4,591	21,078
8	2,602	1,845	6,771	3,404	4,801	4,447	19,777
∑	20,495	23,135	52,513	71,191	59,115	43,631	241,935

Проверим правильности вычислений:

Расчёты произведены верно.

Значит линейный вид функции следующий:

Параметры аппроксимирующей функции и следующие:

Таким образом, вид аппроксимирующей функции, полученный МНК:

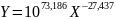
2. ОПРЕДЕЛЕНИЯ ПОГРЕШНОСТИ ПРЕДСКАЗАНИЯ ПОСТРОЕННЫМ УРАВНЕНИЕМ РЕГРЕССИИ РЕЗУЛЬТАТОВ ОПЫТОВ

Оценим значимость полученного уравнения регрессии:

Сначала рассчитаем дисперсию , характеризующую разброс значений относительно среднего значения , причём . Затем рассчитаем остаточную дисперсию , характеризующую разброс значений относительно линии регрессии. Промежуточные расчёты выполним в табличной форме (табл. 3). Тогда:

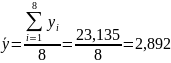
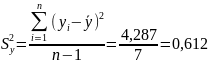
Таблица 3 - Табличная форма для вычисления общей и остаточной дисперсий

№ опыта
1	2,522	3,903	3,975	-0,072	0,005	1,011	1,023
2	2,531	3,813	3,727	0,086	0,007	0,921	0,848
3	2,544	3,398	3,382	0,016	0,000	0,506	0,256
4	2,556	3,000	3,046	-0,046	0,002	0,108	0,012
5	2,568	2,778	2,720	0,058	0,003	-0,114	0,013
6	2,580	2,398	2,402	-0,004	0,000	-0,494	0,244
7	2,591	2,000	2,092	-0,092	0,009	-0,892	0,795
8	2,602	1,845	1,791	0,054	0,003	-1,047	1,096
∑	20,495	23,135	-	-	0,030	-	4,287

Тогда экспериментальное значение критерия Фишера примет следующее значение:

Для уровня значимости q = 5 % и числа степеней свободы

табличное значения критерия Фишера F_табл = 4,21.

Так как F_экс>>F_табл, то полученное уравнение регрессии значимо описывает результаты эксперимента на уровне существенно меньше 5 %, т. е. точно.

3. ОСНОВЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ

Оценим коэффициент корреляции данных эксперимента, представленных в таблице 4.

Таблица 4 - Результаты расчёта сумм

№ опыта
1	2,522	3,903	6,363	15,234	9,845
2	2,531	3,813	6,408	14,538	9,652
3	2,544	3,398	6,472	11,546	8,645
4	2,556	3,000	6,535	9,000	7,669
5	2,568	2,778	6,596	7,718	7,135
6	2,580	2,398	6,655	5,750	6,186
7	2,591	2,000	6,714	4,000	5,182
8	2,602	1,845	6,771	3,404	4,801
∑	20,495	23,135	52,513	71,191	59,115

Коэффициент корреляции ρ определяется через отношение угловых коэффициентов и по формуле:

Знак минус указывает на то, что зависимость убывающая.

На рисунке 2 представлены регрессия y по x и регрессия x по y. Обратную регрессию построили угловой коэффициент обратной регрессии. Согласно расчётам прямой регрессии угловой коэффициент , тогда угловой коэффициент обратной регрессии

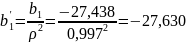
Коэффициент 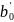регрессии x по y определим с учётом того, что линии регрессии проходят через центр тяжести поля экспериментальных точек. Центр тяжести имеет координаты   , где x — среднее арифметическое значение абсцисс экспериментальных точек, а y — среднее арифметическое значение ординат экспериментальных точек.

Тогда, подставив значения в уравнение регрессии x по y: , то получим:

Отсюда . А значит уравнение регрессии x по y запишется в виде:

Рисунок 2 – Линии прямой и обратной регрессии, построенные для экспериментальных данных таблицы 3.

Как видно из рисунке 2, две регрессии образуют практически не заметные «ножницы», что объясняется очень высоким коэффициентом корреляции экспериментальных данных.