Линейное программирование
.pdfГлава 4. Линейное программирование.
§1. Математические модели в теории исследования операций.
Под термином «исследование операций» будем понимать применение математических количественных методов для обоснования решений во всех областях целенаправленной человеческой деятельности.
Исследование операций – это комплексная математическая дисциплина, занимающаяся построением, анализом и применением математических моделей принятия оптимальных решений при проведении операций.
Операцией называется совокупность взаимосогласованных действий, направленных на достижение определенной цели.
Всякий выбор зависящих от нас параметров называется решением.
В задачах исследования операций имеются фиксированные условия, которые нельзя нарушать, то есть ограничения, налагаемые на решения.
Они образуют множество D – множество допустимых решений.
Решение называется оптимальным, если оно предпочтительнее, лучше по сравнению с другими.
Чтобы сравнивать между собой разные решения, необходим критерий
эффективности.
Критериев эффективности может быть один или несколько. Если в задаче все критерии эффективности могут быть приведены к одному общему критерию эффективности, то задача называется однокритериальной, а общий критерий эффективности – целевой функцией.
= ( ) – зависимость целевой функции от входных параметров. D – множество допустимых решений.
Оптимальным будет решение , обращающее критерий эффективности (целевую функцию) в max или min.
Пример. Имеется ряд предприятий, потребляющих известные виды сырья и ряд сырьевых баз, имеющих сырье. Базы и предприятия связаны путями сообщения. Требуется разработать такой план снабжения предприятий сырьем (с какой базы, в каком количестве, какое сырье), чтобы потребности были обеспечены при минимальных расходах на перевозки.
Операция – процесс составления плана. Решение – определенный план.
Критерий эффективности – суммарные расходы на перевозку. Оптимальное решение – такой план, который дает минимальные расходы. Ограничения – общее количество сырья не превышает количество исходного сырья.
1
В зависимости от вида критерия эффективности (целевой функции) и ограничений рассматривают:
1.Детерминированные модели
Линейное программирование, в том числе транспортная задача;
Целочисленное программирование;
Динамическое программирование.
2.Вероятностные модели
Теория массового обслуживания;
Теория игр;
Календарное планирование;
Модели управления запасами
идр.
§2. Задачи линейного программирования.
Среди задач на отыскание значений параметров, обеспечивающих экстремум функции при наличии ограничений, наложенных на аргументы, наиболее простыми являются задачи линейного программирования.
К задачам линейного программирования относятся такие задачи, в которых
1)целевая функция = ( 1, 2, … , ) линейно зависит от 1, 2, … , .
2)ограничения, налагаемые на 1, 2, … , имеют вид линейных равенств или неравенств относительно 1, 2, … , .
Рассмотрим примеры задач линейного программирования.
2
1. Задача планирования производства (задача использования сырья).
Для изготовления двух видов продукции 1 и 2 используют три вида
сырья 1, 2, 3.
Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, приведены в таблице.
|
|
|
Количество единиц сырья, идущих на |
|
Вид сырья |
|
Запас сырья |
изготовление единицы продукции |
|
|
|
|
1 |
2 |
1 |
|
20 |
2 |
5 |
2 |
|
40 |
8 |
5 |
3 |
|
30 |
5 |
6 |
Прибыль от единицы продукции |
50 |
40 |
||
|
(руб.) |
|
|
|
Требуется составить такой план выпуска продукции, чтобы при ее реализации получить максимальную прибыль.
3
2. Задача составления рациона (задача диеты).
При откорме каждое животное ежедневно должно получать не менее 33 ед. питательного вещества А; не менее 23 ед. питательного вещества В;
не менее 12 ед. питательного вещества С (белки; кальций; углеводы). Для откорма используются три вида кормов: 1, 2, 3
Содержание количества единиц питательных веществ в 1 кг каждого вида корма и стоимость 1 кг корма даны в таблице.
|
Количество единиц питательных |
||||
Питательные вещества |
|
веществ в 1 кг корма |
|
||
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
A |
4 |
|
3 |
|
2 |
B |
3 |
|
2 |
|
1 |
C |
1 |
|
1 |
|
2 |
Стоимость 1 кг корма |
20 |
|
20 |
|
10 |
Требуется составить такой пищевой рацион, чтобы стоимость его была минимальной.
4
§3. Постановка задачи линейного программирования (ЗЛП) и различные формы ее записи.
Дана целевая функция |
|
|
|
|
|
|
|
|
|
|
|
|
, , … , |
|
|
= |
|
|
+ |
|
+ + |
или |
|||
1 2 |
|
1 |
1 |
|
2 |
2 |
|
|
|
|
||
|
|
|
|
|
= |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
и система ограничений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
+ + |
|
≤ |
|
||||
|
11 1 |
|
12 |
2 |
|
1 |
|
1 |
|
|||
|
|
+ |
|
+ + |
|
≥ |
|
|||||
|
21 |
1 |
|
22 |
2 |
|
2 |
|
2 |
|
||
|
… … … … … … … … … … … … … … . . |
|
||||||||||
|
1 |
+ |
2 |
+ + |
|
≤ |
|
|||||
|
|
1 |
|
2 |
|
|
|
|
||||
|
|
|
≥ 0, ≥ 0, … , |
≥ 0 |
|
|||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ ≥ ; = ( = 1, … , ) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
=1
≥ 0 ( = 1, … , )
Требуется найти такие значения переменных 1, 2, … , , которые удовлетворяют системе ограничений и максимизируют (минимизируют) целевую функцию.
= ( 1, 2, … , ) − входные параметры; решения (план). Решение = ( 1, 2, … , ) называется допустимым, если оно удовлетворяет системе ограничений.
− множество допустимых решений.
Допустимое решение = ( , , … , ) называется оптимальным, если при |
||
1 |
2 |
|
данном решении целевая функция принимает максимальное (минимальное) значение.
Если находим max, то это задача максимизации; если min, то задача минимизации.
Замечания.
1. В системе ограничений можно перейти к неравенствам одного вида (≥ 0 или ≤ 0), умножив обе части соответствующих неравенств на (-1).
2. Задачи максимизации и минимизации легко сводятся одна к другой: Если − оптимальное решение задачи максимизации целевой функции на множестве , то это же будет оптимальным решением задачи минимизации целевой функции = −
5

Итак, задача линейного программирования (ЗЛП) может быть сформулирована следующим образом:
1. Найти значения переменных 1, 2, … , , которые удовлетворяют
ограничениям
≤ ( = 1, … , )
=1
≥ 0 ( = 1, … , )
и обращают в max целевую функцию
|
, |
, … , = |
|
|
→ |
1 |
2 |
|
|
|
|
=1
Это общая постановка задачи линейного программирования.
2. Запишем в матричной форме. |
|
|
|
|||
Обозначим: |
|
|
|
|
|
|
11 |
… |
1 |
1 |
|
|
|
= … |
… . |
… ; = |
; = , … , ; = |
1 |
||
|
||||||
|
|
… |
|
|
1 |
|
1 |
|
|||||
|
|
|
|
|
||
|
|
|
|
|
|
|
Найти вектор , который удовлетворяет ограничениям
∙ ≤
≥ 0
иобращает в max целевую функцию
= ∙ →
Это общая постановка задачи линейного программирования в матричной форме.
Любую задачу линейного программирования (ЗЛП) можно свести к
стандартной (канонической) форме, так называемой основной задаче линейного программировании (ОЗЛП):
Найти значения 1, 2, … , , которые удовлетворяют ограничениям
|
|
|
|
+ |
+ + |
|
= |
|
|
||
|
|
11 1 |
12 |
2 |
1 |
|
1 |
|
|
||
|
|
|
+ |
+ + |
|
= |
|
|
|||
|
|
21 |
1 |
22 |
2 |
2 |
|
2 |
|
|
|
|
|
… … … … … … … … … … … … … … . . |
|
|
|||||||
|
|
1 |
+ |
+ + |
|
= |
|
|
|||
|
|
|
1 |
2 |
2 |
|
|
|
|
||
|
|
|
|
|
≥ 0, ≥ 0, … , |
≥ 0 |
|
|
|||
|
|
|
|
1 |
|
2 |
|
|
|
|
|
и обращают целевую функцию в max |
|
|
|
|
|
||||||
|
= , |
|
, … , |
= |
+ + + |
|
→ |
||||
|
1 |
2 |
|
|
1 1 |
2 |
2 |
|
|
|
|
Задача линейного программирования в стандартной (канонической) форме.
6
|
|
Итак |
|
|
= ∙ → |
− общая форма записи ЗЛП |
|
∙ ≤ − ограничения |
|||
|
|||
≥ 0 |
|
|
|
|
= ∙ → |
|
|
∙ = − ограничения |
− стандартная (каноническая) форма записи ЗЛП |
||
≥ 0 |
|
(ОЗЛП) |
|
Покажем, как от общей формы записи перейти к стандартной форме.
Задача 1.
2 1 + 5 2 ≤ 20
8 1 + 5 2 ≤ 40
5 1 + 6 2 ≤ 30
1 ≥ 0, 2 ≥ 0
Введем дополнительные переменные 3, 4, 5 (равные разности между правыми и левыми частями неравенств). Тогда
2 1 + 5 2 + 3 = 20 8 1 + 5 2 + 4 = 40
5 1 + 6 2 + 5 = 30
1 ≥ 0, 2 ≥ 0, 3 ≥ 0, 4 ≥ 0, 5 ≥ 0
Задача 2.
4 1 + 3 2 + 2 3 ≥ 33 3 1 + 2 2 + 3 ≥ 231 + 2 + 2 3 ≥ 121 ≥ 0, 2 ≥ 0, 3 ≥ 0
Введем дополнительные переменные 4, 5, 6 (равные разности между левыми и правыми частями неравенств). Тогда
4 1 + 3 2 + 2 3 − 4 = 33 3 1 + 2 2 + 3 − 5 = 231 + 2 + 2 3 − 6 = 12
1 ≥ 0, 2 ≥ 0, 3 ≥ 0, 4 ≥ 0, 5 ≥ 0, 6 ≥ 0
7
§4. О методах решения задачи линейного программирования.
Дана целевая функция |
|
|
|
|
|
|
|
|
|
|
|
|
, , … , |
= |
|
+ |
|
+ + |
|
||||||
1 2 |
|
|
1 1 |
|
2 2 |
|
|
|
|
|||
и система ограничений |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ + |
|
|
≤ |
|||||
|
11 |
1 |
|
|
12 |
2 |
|
1 |
|
1 |
||
|
|
+ |
+ + |
2 |
|
≤ |
||||||
|
21 |
1 |
|
|
22 |
2 |
|
|
|
2 |
||
|
… … … … … … … … … … … … … … . . |
|||||||||||
|
1 |
+ |
2 |
+ + |
|
|
≤ |
|||||
|
|
1 |
|
|
2 |
|
|
|
|
|||
|
|
|
|
≥ 0, |
≥ 0, … , |
≥ 0 |
||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ + |
|
= |
||||||
|
11 |
1 |
|
|
12 |
2 |
|
1 |
|
1 |
||
|
|
+ |
+ + |
|
= |
|||||||
|
21 |
1 |
|
|
22 |
2 |
|
|
2 |
|
2 |
|
|
… … … … … … … … … … … … … … . . |
|||||||||||
|
1 |
+ |
2 |
+ + |
|
|
= |
|||||
|
|
1 |
|
|
2 |
|
|
|
|
|||
|
|
|
|
≥ 0, |
≥ 0, … , |
≥ 0 |
||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
Можно считать, ≥ 0, = 1, … . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Требуется найти такие значения переменных 1, … , , которые удовлетворяют системе ограничений и максимизируют (минимизируют) целевую функцию.
При использовании классических методов возникают непреодолимые вычислительные сложности, поэтому для решения задач линейного программирования (ЗЛП) нужны специальные методы.
§5. Геометрический (графический, градиентный) метод решения ЗЛП.
I. Линии уровня, градиент.
Опр. Линией уровня функции , … , |
называется множество точек |
|||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
n-мерного пространства, в которых эта функция сохраняет постоянное |
||||||||||||||||||
значение, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
, … , |
|
|
= |
|
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
Опр. Градиентом функции |
, … , |
|
|
|
называется вектор, проекциями |
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
которого служат значения частных производных этой функции: |
|
|
||||||||||||||||
|
|
|
|
|
= |
|
|
|
, … , |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Если |
, … , 0 − некоторая фиксированная точка, то |
|
|
|||||||||||||||
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
, … , |
|
|
|
− градиент функции , … , |
в точке |
||||||||||
|
|
0 |
||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
0 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Свойства: градиент перпендикулярен к линиям уровня и указывает направление наискорейшего возрастания функции в данной точке 0.
8
В качестве целевой функции возьмем |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1, 2 |
|
= 1 1 + 2 2 |
|
|
|
|
|
|
||||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
+ |
|
|
|
= − линии уровня функции |
|
, |
= |
|
+ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
1 |
2 |
2 |
|||
2) |
|
|
= ; |
|
|
= . Значит, = |
, |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
1 2 |
|
2 |
|
|
|
1 2 |
|
|
|
|
|
|
|
|||||||
|
|
= |
|
|
, |
|
− градиент функции |
, |
= |
|
+ |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
1 |
2 |
2 |
|
|
|
||
Итак, градиент функции 1, 2 |
|
|
= 1 1 + 2 2 есть вектор, постоянный во |
|||||||||||||||||||
всех точках области определения функции и перпендикулярен линиям |
|
|||||||||||||||||||||
уровня функции. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
II. ЗЛП с системой ограничений в виде неравенств и |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
числом переменных = . |
|
|
|
|
|
|
|
|||||
Система ограничений |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
11 1 + 12 2 |
≤ 1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
… … … … … … … … . . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
≥ 0, 2 ≥ 0 |
|
|
|
|
|
|
|
|||
Целевая функция |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1, 2 |
= 1 1 |
+ 2 2 |
→ |
|
|
|
|
|
||||
Каждое неравенство системы ограничений геометрически определяет |
|
|||||||||||||||||||||
полуплоскость с граничной прямой |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
+ |
= , = 1, … , |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 1 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
Условия 1 |
≥ 0, 2 ≥ 0 определяют 1-й координатный угол плоскости О 1 2 |
|||||||||||||||||||||
Таким образом, система ограничений определяет область D – область |
|
|||||||||||||||||||||
допустимых решений, которая получается в результате пересечения |
|
|||||||||||||||||||||
полуплоскостей и первого координатного угла. |
|
|
|
|
|
|
|
|||||||||||||||
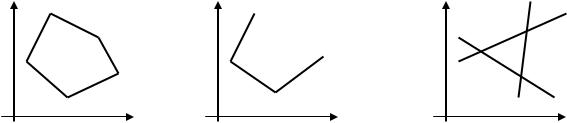
|
В качестве D области можем иметь: |
|
|
|
|
|
|
|
|
|||||||||||||
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||
0 |
1 |
0 |
1 |
0 |
1 |
В частности, можем иметь также точку, луч, отрезок.
9
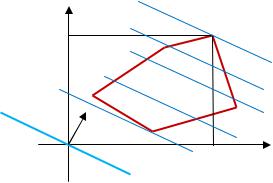
Рассмотрим случай, когда область D – область допустимых решений есть ограниченный многоугольник; будем называть его многоугольник решений.
2 |
|
|
|
B |
|
2 |
|
|
|
D |
|
|
|
|
0 |
|
|
|
1 |
1 |
|
1 1 + 2 2 = 0 |
|
Требуется: среди всех точек многоугольника найти такую точку, координаты
которой максимизирует целевую функцию 1, 2 |
= 1 1 + 2 2. |
||
Линии уровня 1 1 |
+ 2 2 = − семейство параллельных прямых. |
||
При переходе от точек одной линии к точкам другой линии значение |
|||
функции 1, 2 |
меняется (а вдоль одной линии постоянно). |
||
Для нахождения точки = ( , ) , в которой функция принимает |
|||
|
1 |
2 |
|
максимальное значение надо двигаться в направлении возрастания значений целевой функции (по градиенту этой функции).
Из т. О(0;0) выходит вектор = ( 1; 2), направление которого определяет направление возрастания целевой функции 1, 2 = 1 1 + 2 2. Строится линия уровня 1 1 + 2 2 = 0, которую передвигают в направлении вектора до тех пор, пока она не пройдет через последнюю общую точку линии уровня с областью D. В этой точке с координатами ( 1, 2) целевая функция принимает максимальное значение.
Порядок решения ЗЛП геометрическим методом.
1. Построить D – многоугольник решений системы ограничений (множество допустимых решений).
2.Построить вектор = ( 1; 2) и одну из линий уровня, например, 1 1 + 2 2 = 0.
3.Параллельным перемещением прямой 1 1 + 2 2 = 0 в направлении
= ( 1, 2) , в которой целевая функция
1, 2 = 1 1 + 2 2 достигает максимального значения.
− точка пересечения двух прямых, то для нахождения координат
точки необходимо решить систему двух соответствующих уравнений.
10
