
|
|
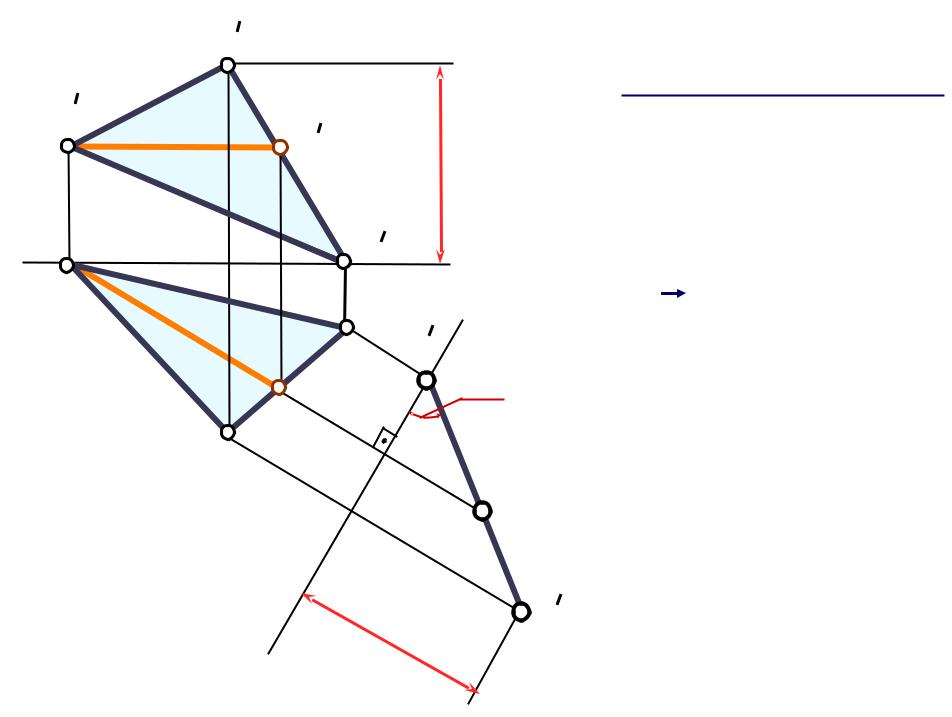
Задача 1 |
Плоскость общего положения |
|
Дано: |
|||||
|
|
|
bпреобразовать в проецирующую |
|||||||
|
|
|
Q(∆ABC) - |
|||||||
|
|
а |
|
|
|
|
|
|
плоскость общего положения |
|
|
|
|
|
|
|
|
Преобразовать в положение |
|||
|
|
|
1 |
|
Z |
|
фронтально-проецирующей |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
Для преобразования плоскости во фронтал |
|||
|
|
|
|
|
c |
|
но проецирующую необходимо заменить |
|||
x |
V |
|
|
|
|
плоскость проекций V на V1 , расположив |
||||
|
|
|
|
|
ее перпендикулярно плоскости Q, т.е. |
|||||
H |
а |
|
|
c |
|
|
|
|
V / H V1 / H, V1 H, V1 Q |
|
|
|
|
|
с1 |
|
1. Предварительно строим главную |
||||
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
линию-горизонталь (А1). |
|||
|
|
|
|
|
|
|
|
2. Проводим новую ось проекций Х1 |
||
|
|
b |
|
|
|
|
|
перпендикулярно горизонтальной |
||
|
|
|
|
а‘1 = |
|
проекции горизонтали X1 а1, |
||||
α -угол наклона |
|
|
|
3. Проводим из незаменяемых |
||||||
|
|
|
проекций точек линии связи к |
|||||||
плоскости Q |
|
|
|
1‘1 |
новой оси Х и откладываем |
|||||
к плоскости H. |
|
|
|
|||||||
|
|
|
координаты 1Z точек. |
|||||||
|
|
|
H |
|
|
Z |
|
b1 |
В результате |
|
|
|
|
V |
|
|
|
преобразования получили |
|||
|
|
|
x1 |
|
|
|
|
а1’b1‘c1’ - прямая, т.е |
||
|
|
|
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
Q(∆ABC) - фронтально |
||
|
|
|
|
|
|
|
|
|
проецирующая плоскость. |
|
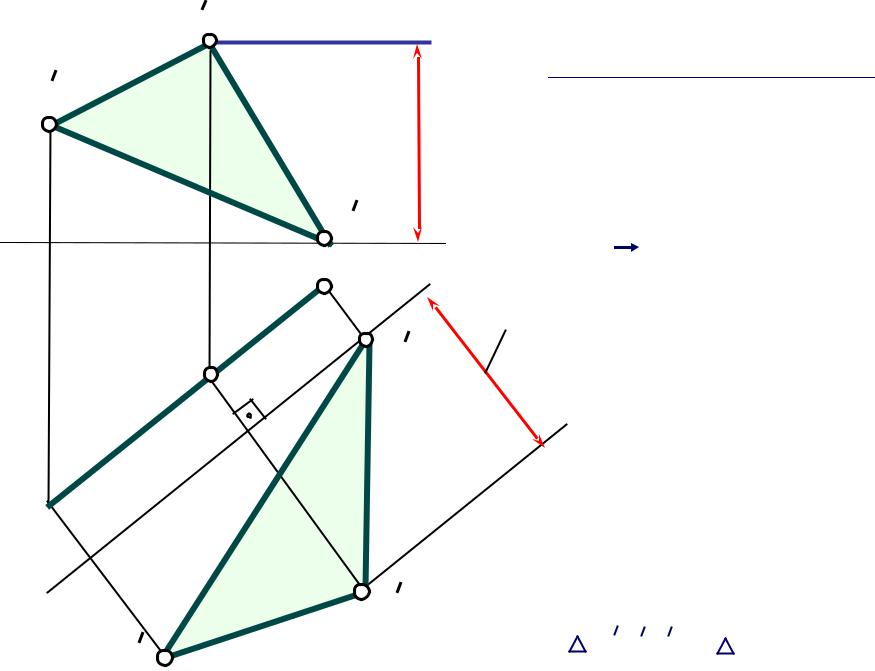
Задача 2
а
x HV
Плоскость проецирующую преобразовать Дано: |
|
||||||
bв плоскость уровня. |
|
Q(ΔABC) H - плоскость |
|||||
|
|
|
|
|
горизонтально-проецирующая |
||
|
|
|
B |
|
|
Преобразовать в |
|
|
|
|
Z |
|
|
положение |
|
|
|
|
|
|
|
фронтально |
Решение |
|
|
|
|
|
|
проецирующей |
|
|
|
|
|
|
|
|
|
|
|
c |
|
Переходим от системы V/H к |
|||
|
|
|
cистеме V1 /H. |
|
|||
|
c |
|
|
Z |
|
V/H V1 /H, V1 H, V1 //Q |
|
|
|
|
|
||||
|
|
|
|
1. Строим новую ось x1 |
|||
|
|
|
|||||
|
|
|
|
|
|||
|
|
|
c1 |
B |
|
||
b |
|
|
|
|
параллельно проекции аbc |
||
|
|
|
|
||||
|
|
|
|
x1 аbc |
|
||
|
|
|
|
|
|
2. Проводим из точек а, b, с |
|
|
|
|
|
|
|
линии связи к оси x1 |
|
а
x1 |
H |
V |
|
|
1 |
|
3. Откладываем |
|
координаты Z |
|
точек от новой оси |
b1 |
проекций |
В результате преобразования |
|
а1 |
b c |
|
/ а1 1 1/ = / ABC / |
|
|
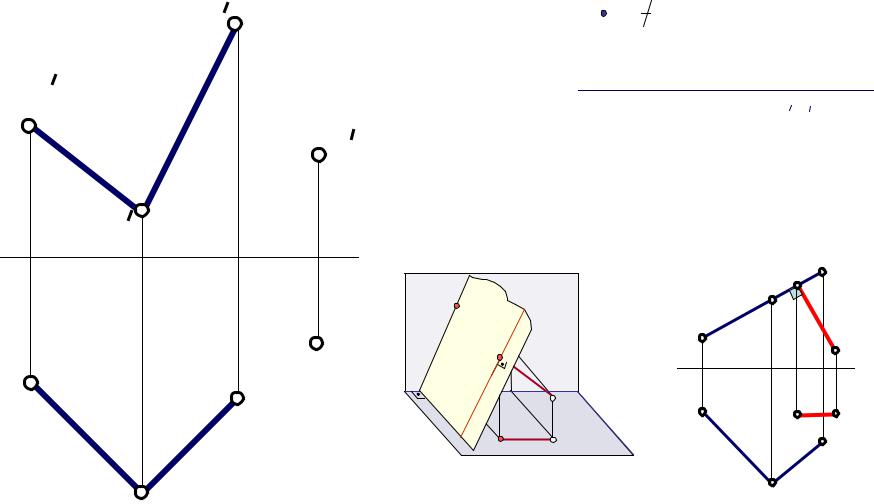
Задача 1 |
|
|
|
|
|
|
|
|
|
Дано: |
|
|
|
||||
Определить расстояние от точки K до плоскости Q |
|
|
|
|
|
||||||||||||||
|
BC) |
|
|
|
|||||||||||||||
|
|
c |
|
|
|
|
|
|
|
|
Q(AB |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
( )K |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
KN-расстояние от |
|
|
|||||||
а |
|
|
|
|
|
|
|
|
|
|
точки K до плоскости Q |
||||||||
|
|
|
|
|
|
|
|
|
|
|
/KN /- ? |
kn -? |
k |
|
- ? |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
k |
|
|
|
|
|
|
|
|
Анализ решения n |
|
|||||||
|
|
Рассмотрим пространственную картину и эпюр из |
|||||||||||||||||
|
b |
|
которых видно,что расстояние от точки до плоскост |
||||||||||||||||
X v |
|
проецируется в натуральную величину когда заданная |
|||||||||||||||||
|
плоскость будет проецирующей. |
|
|
c‘ |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
H |
|
|
|
V |
|
|
|
|
|
Q |
|
|
|
|
|
b‘ |
n’ |
|
|
|
|
|
|
|
г |
|
|
|
|
|
|
|
|
|
|
||||
|
|
k |
|
|
n’ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
р |
|
|
|
|
|
а‘ |
|
|
|
|||||
|
|
|
|
|
|
и |
k‘ |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
k’ |
|||||
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
аN |
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
л |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
ь |
|
|
|
|
|
|
|
|
||
а |
|
X |
|
|
|
|
|
|
ль |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
н |
т |
а |
K |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
k |
||||||
|
|
|
|
|
|
ро |
|
|
|
|
|
|
а |
|
|
||||
|
|
|
|
ф |
|
|
|
n |
k |
|
|
|
а |
|
|||||
|
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
c |
||||
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bb |
c |
|||
|
b |
Для решения задачи необходимо |
|
||||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
плоскость Q преобразовать в |
|
|
|
|
|
||||||||||||
|
|
положение проецирующей. |
|
|
|
|
|
|
|
||||||||||
|
|
|
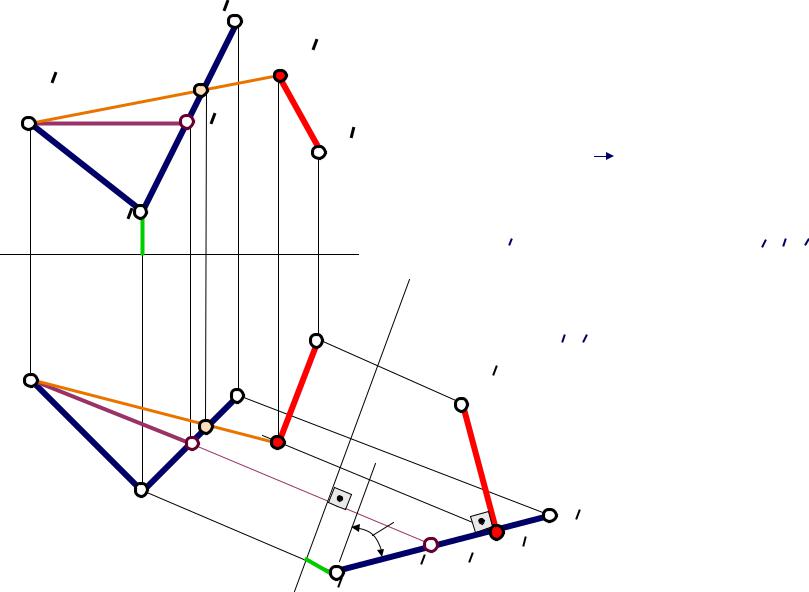
Задача 1 |
|
|
|
|
|
|
|
||
|
c |
|
|
|
|
|
|
Решение |
|
|
||
|
n |
|
1. Строим в плоскости горизонталь А1 |
|||||||||
|
|
|
||||||||||
а |
|
|
и преобразуем плоскость Q в положение |
|||||||||
|
|
|
фронтально проецирующей |
|
|
|
|
|||||
|
1 |
|
k |
|
|
А1-горизонталь |
|
|
|
|||
|
|
|
|
|
V/H |
V1/H, V1 |
H, |
|
|
|||
|
b |
|
|
|
|
|
V1 |
Q, X1 |
а1 |
|
|
|
X v |
|
|
|
2. Опускаем перпендикуляр из точки |
||||||||
|
|
X1 |
K( |
)kна след плоскости |
b а c |
1 |
||||||
H |
|
|
|
|
1 |
|
|
|
1 |
1 |
||
|
|
|
Получили: |
|
|
|
|
|
||||
|
|
|
k |
H V1 |
|
|
|
|
|
|||
|
|
|
|
|
KN |
V//1 – фронтальная прямая, т.е. |
||||||
|
|
c |
|
|
| |
k1|n=1 |KN|, поэтому |
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
k1 kn |
// |
|
|
|
|
|
||
а |
|
|
|
X1 |
|
|
|
|
|
|||
|
|
|
|
|
Фронтальную проекцию точки n |
|||||||
|
1 |
n |
|
|
|
строим из условия ее принадлежнос |
||||||
|
|
|
|
прямой АN плоскости Q |
|
|||||||
|
b |
|
|
|
|
n1 |
c1 |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
||
|
|
|
b1 |
а1 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
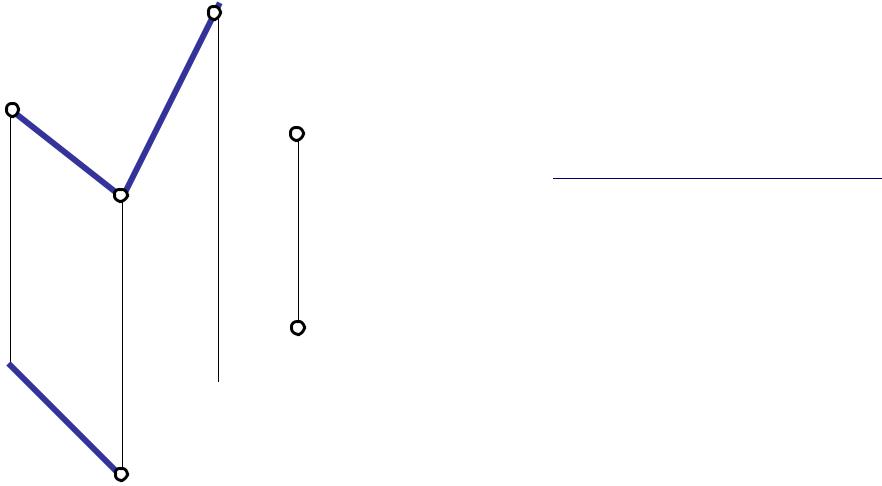
Задача 2
|
|
c’ |
|
Построить точку Е симметричную точке К |
||
|
|
|
|
|||
а’ |
|
|
относительно плоскости Q. |
|||
|
k’ |
K( |
Дано: |
|||
|
|
|
) |
|||
|
|
|
|
|
Q(AB |
BC) |
|
|
|
|
|
|
|
X v |
b’ |
|
|
k,k’ |
|
|
|
|
е -? |
e’ -? |
|||
|
|
|
|
|
||
H |
|
|
|
|
|
|
k
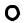 с а
с а 
b
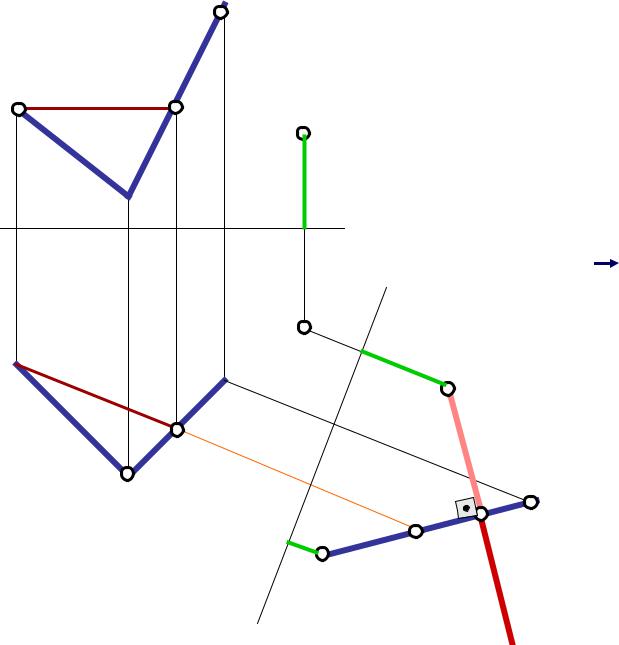
c’ |
|
а’ |
|
1’ |
k’ |
|
X Hv b’
k
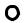 с а
с а 
1
b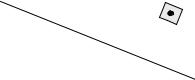
b’1
Задача 2
Решение
Для решения необходимо преобразовать плоскость Q в положение проецирующей. Искомая точка лежит на перпендикуляре, опущенном из точки К на след плоскости.
1. Преобразуем плоскость Q в положение фронтально проецирующей
X |
V/H |
V1/H, V1 H, |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
V |
|
Q, X а1, |
|
|
|
|
H V |
|
|
|
|
|
||
1 |
1 |
|
1 |
|
|
|
|
k’1 |
A1-горизонталь |
|
|
|
|
||
|
2. Опускаем перпендикуляр |
||||||
|
|
||||||
|
|
из точки k’на |
b’ |
а’ |
c’ |
1 |
|
|
|
|
1 |
1 |
1 |
|
|
|
c’1 |
и отмечаем точку e’1на |
|||||
|
расстоянии n’1e’1 = n’1k’1 |
||||||
а’1 |
n’1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 e’1
e’1
c’ |
e’ |
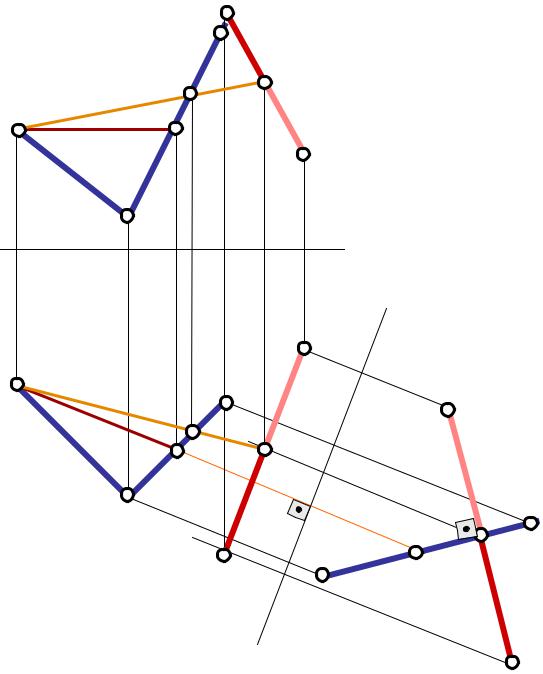
Задача 2 |
|
|
|
n’ |
|
|
|
||
а’ |
|
3. Строим проекции точки Е |
|||
|
|
в исходной системе координат |
|||
1’ |
|
k’ |
|||
|
KN V |
– фронтальная прямая, |
|||
|
|
||||
|
|
|
// 1 |
|
|
X v b’ |
|
|
т.е. |
|
|
|
|
| k’1n’| =1 |KN| = |
|n’1e’|1= |NE| |
||
H |
|
X1 |
поэтому |
|
|
|
|
|
|||
с |
|
k H V1 |
kn X1 // |
|
|
|
|
k’1 |
|
|
|
а |
n |
|
|
|
|
1 |
c’1 |
|
|||
b |
|
|
|
||
|
|
n’1 |
|
|
|
e |
|
|
|
|
|
|
а’1 |
|
|
||
|
|
b’1 |
e’1 |
|
|
|
|
|
|
||
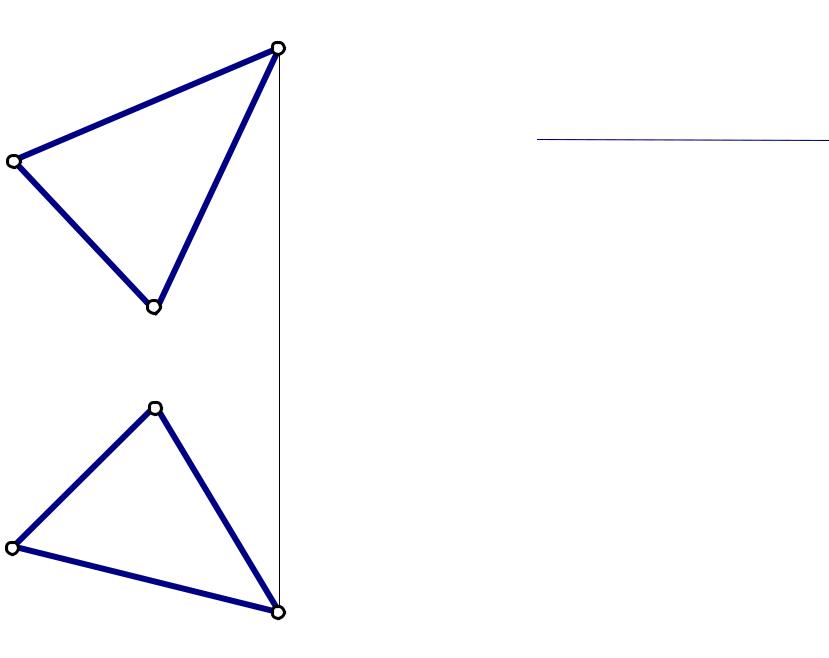
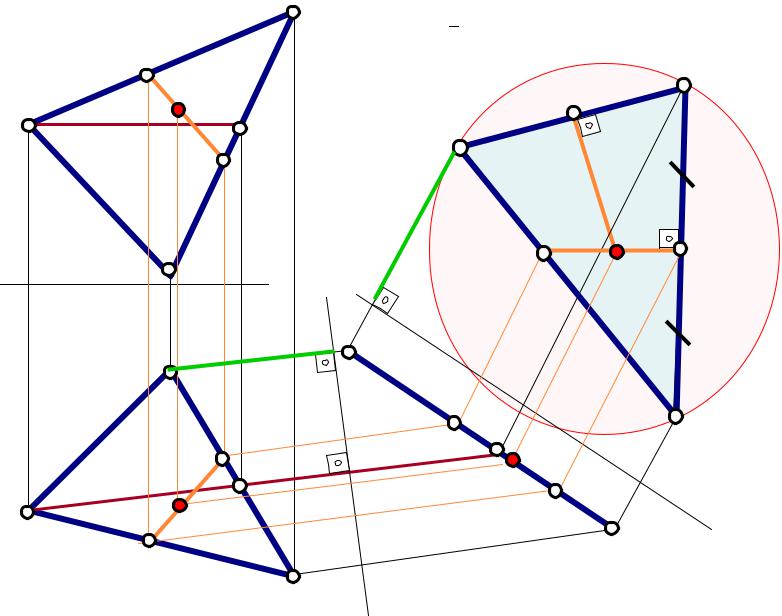
Задача 3
Найти центр окружности, описанной b’ Относительно трех точек А, В, С.
|
|
|
|
|
Дано: |
а’ |
|
|
|
Q ( A, B, С) |
|
|
|
|
О–центр описанной |
||
|
|
|
|
|
окружности о-? о’ -? |
|
|
|
|
|
Анализ решения |
X v |
|
|
c’ |
Для решения задачи необходимо преобразовать |
|
|
|
плоскость, заданную тремя точками, в положение |
|||
|
|
||||
|
|
|
|
|
плоскости уровня (две перемены плоскостей |
H |
|
|
|
||
|
|
c |
|
|
проекций). |
|
|
|
|
Далее на натуральной величине плоскости |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
определить центр описанной окружности как точку |
|
|
|
|
|
пересечения перпендикуляров, проведенных |
|
|
|
|
|
через середины сторон. |
а |
|
|
|
Задача завершена после возврата полученной точк |
|
|
|
|
|||
|
|
|
|
|
в исходную систему плоскостей проекций. |
b |
|
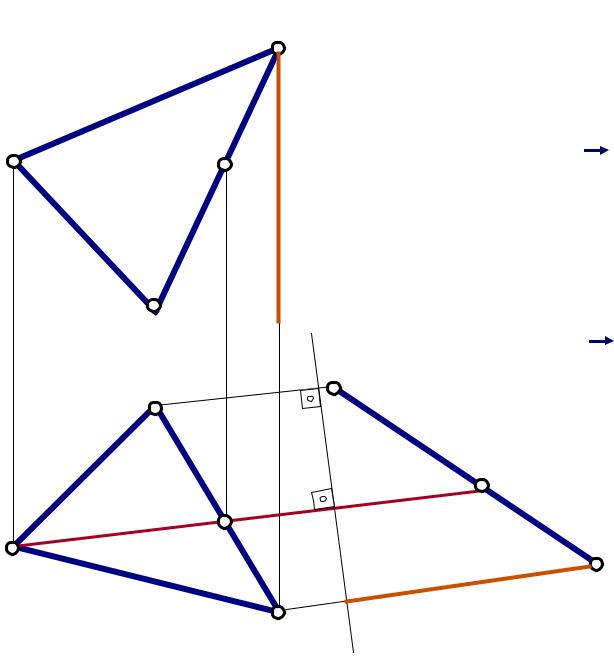
Задача 3 |
b’ |
Решение |
|
1. Преобразуем плоскость Q в |
|
положение фронтально проецирующей |
а’ |
|
|
1’ |
|
|
V/H |
V1/H, V1 |
H, |
||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
V |
Q, X |
а1, |
||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
A1-горизонталь |
||||||
X v |
|
c’ |
|
2. Преобразуем плоскость Q в положение |
||||||||||
|
X |
плоскости уровня (горизонтальную) |
||||||||||||
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
H |
|
|
|
|
|
V1/H V1/H1 , V1 H, |
||||||||
|
|
|
|
H V1 |
c1’ |
|||||||||
|
|
c |
|
|
|
|
H1 |
|
Q, X2 |
|
|
b ’ |
||
|
|
|
|
|
// |
// |
1 |
а1’с1’ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
а1’ |
|
1 |
а |
b1’ |
|
|
|
b |
|
|
|
Задача 3 |
|
|
|
|
|
|
b’ |
3. Строим центр О описаной окружности |
||||
|
f’ |
4. Выполним возврат точки О в систему Н |
|||||
|
|
|
|
|
|
|
|
|
|
О EF |
|
|
а1 |
||
|
|
|
|
|
|||
а’ |
o’ |
|
c1 |
|
|
||
1’ |
|
|
|
|
|||
|
|
e’ |
|
|
o1 |
|
|
X v |
c’ |
|
e1 |
f |
1 |
||
|
X |
|
|
|
|||
H |
|
|
1 |
|
|
|
|
|
|
H V1c1’ |
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
e |
|
e1’а ’ |
|
b1 |
||
|
1 |
1 |
o1’f1’ |
|
|||
|
|
|
|||||
а |
|
|
V H1 |
||||
o |
|
|
|
|
|||
|
f |
|
|
|
b1’ |
1 X2 |
|
|
b |
|
|
|
|||
|
|
|
|
|
|
||
Задача 4 |
Через точку А провести прямую |
|
под углом 400 к оси Х |
z
а’
X vH
а
yH
Дано:
A(а, )а’
АК– прямая под углом 400 к оси Х
аk-? а’к’ -?
Алгоритм решения
1.Зададим плоскость точкой А и отрезком оси Х;
2.2. Определим натуральную величину плоскости;
3.На натуральной величине построим прямую из точки А под углом 400 к оси Х;
4. Выполним возврат этой прямой в исходную систему координат.
