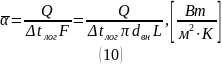САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ПЕТРА ВЕЛИКОГО

Институт Энергетики

Высшая школа атомной и тепловой энергетики

Лабораторная работа ТМО-5

"Исследование теплоотдачи при вынужденном турбулентном движении воздуха в трубах"

Студент гр. 3231401/20002 ______Школьников А.С.

Студент гр. 3231401/20002 ______Сирош С.А.

Преподаватель ________________ Павлов А. В.

Содержание

1. Введение 3

2. Описание установки 6

3. Результаты эксперимента 8

5. Вывод 17

1. Введение

Рассмотрим конвективный теплообмен в круглой трубе, поверхность которой поддерживается при постоянной температуре 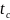, превышающей температуру протекающего по трубе воздуха. Условие =𝑐𝑜𝑛𝑠𝑡 обеспечивается тем, что труба окружена рубашкой нагрева, в которую поступает сухой насыщенный водяной пар при давлении, близком к атмосферному.

При конвективном теплообмене между средой с температурой 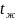и стенкой с температурой тепловой поток 𝑄 определяется законом Ньютона:

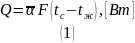
где 𝐹 - поверхность теплообмена, 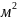; 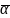- средний коэффициент теплоотдачи, Вт/( ·К). Тепловой поток 𝑄 при условии = 𝑐𝑜𝑛𝑠𝑡 можно определить двумя способами:

1. как разность потоков энтальпии сухого насыщенного пара и конденсата в изобарном процессе:

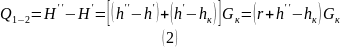
где ℎ′ и ℎ′′ – энтальпии насыщенной жидкости и сухого насыщенного пара, Дж/кг; 𝑟 – скрытая теплота парообразования, Дж/кг; ℎ′ – энтальпия кипящей жидкости, Дж/кг; 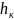– энтальпия конденсата, Дж/кг; 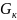– количество сконденсировавшегося (в результате теплообмена между паром и исследуемым воздушным потоком) пара, кг/с.

Обычно конденсат не успевает охладиться существенно ниже температуры насыщения. В этом случае можно считать, что ≈ ℎ ′ ;

2. по изменению энтальпии потока воздуха:

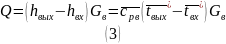
где 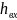, 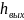– удельные энтальпии воздуха на входе и выходе из трубы, соответственно, Дж/кг; 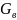– массовый расход воздуха, кг/с;

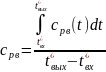− средняя изобарная теплоёмкость воздуха;

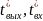− температуры торможения воздуха на входе и выходе из трубы.

В результате теплообмена воздушного потока с нагретой стенкой местное значение температуры изменяется по радиусу. Следовательно, для неизотермического потока на 3 выходе из рабочего участка необходимо найти среднюю температуру 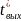, которая определяется из полной энтальпии потока в выходном сечении канала

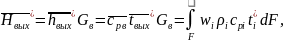
откуда

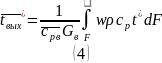
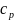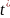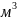где значения изобарной теплоёмкости , Дж/(кг·К), температуры торможения , плотности 𝜌, кг/ , и скорости 𝑤, м/с, являются функциями, изменяющимися по площади сечения трубы 𝐹, . Как известно, температура торможения связана с термодинамической температурой соотношением

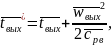
где 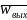- средняя скорость воздуха в выходном сечении трубы. При малых скоростях потока, когда воздух можно считать несжимаемой средой (при условии, что число Маха меньше 0,3), 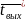≈ 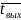. Среднемассовый расход воздуха (кг/с) рассчитывается по формуле:

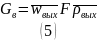
а скорость усредняется по площади сечения трубы:

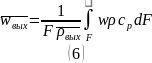
Первый способ определения теплового потока требует учитывать тепловые потери в разных элементах парового тракта, что не всегда удобно. В этом смысле второй способ предпочтительнее, поэтому он и применяется в данной работе. Кроме того, такой подход позволяет познакомиться с методикой осреднения скоростей и температур в однородном газовом потоке.

Во время опыта температура стенки поддерживается практически неизменной: подогрев трубы насыщенным паром обеспечивает это условие.

Коэффициент теплоотдачи от водяного пара к трубе достигает (7...12)·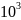 Вт/( ·К). Труба рабочего участка изготовлена из меди, обладающей высокой теплопроводностью (𝜆 = 385 Вт/(м·К)). В связи с этим полное термическое сопротивление системы пар–воздух будет практически определяться термическим сопротивлением от внутренней поверхности трубы к воздуху, а температура этой поверхности будет незначительно отличаться от температуры насыщенного пара 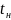, поэтому можно принять ≈ .

При установившемся тепловом режиме и неизменном (по длине трубы) коэффициенте теплоотдачи температура воздуха, протекающего по трубе, изменяется по экспоненциальному закону. Среднелогарифмический перепад между температурам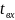и и

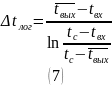
Зная величину 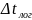, можно рассчитать среднюю температуру воздуха на рабочем участке:

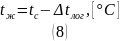
Поверхностью нагрева служит внутренняя поверхность трубы

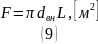
где 𝐿 – длина рабочего участка, м.

Значение коэффициента теплоотдачи определяется для каждого режима по закону Ньютона: