Лабораторна робота №4. Теорія двоїстості та аналіз лінійних моделей оптимізаційних задач

Виконала:

Студентка 3 курсу, 1 групи

Економіка підприємства

Стешенко Тетяна

Тема: Теорія двоїстості та аналіз лінійних моделей оптимізаційних задач Мета: Оволодіти методом побудови та розв’язку двоїстих задач. Завдання: 1.побудувати двоїсту задачу до задач запропонованих в доданому файлі "Двоїсті"(варіанти) 2.розвязати симплексним методом задачі лінійного програмування у двоїстій скороченій симплексній таблиці використовуючи модифіковані Жорданові виключення 3. Виписати результати розв'язки двох спряжених задач з таблиці.

Варіант - 1

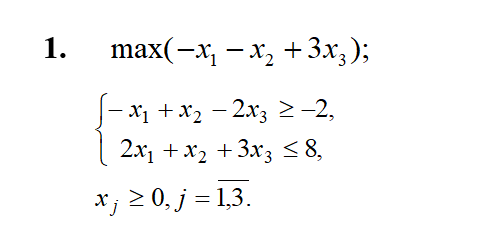
Двоїста задача лінійного програмування

Розв’яжемо пряму задачу лінійного програмування симплекс-методом з використанням симплексної таблиці. Оскільки в правій частині присутні негативні значення, помножимо відповідні рядки на (-1).

Визначимо максимальне значення цільової функції : при наступних умовах-обмеженнях:

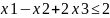
Для побудови першого опорного плану систему нерівностей перетворимо в систему рівнянь шляхом введення додаткових змінних (перехід до канонічної форми).

У 1-й нерівності (≤) вводимо базисну змінну x4. У 2-й нерівності (≤) вводимо базисну змінну x5.

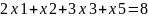
Матриця коефіцієнтів A=aij​ цієї системи рівнянь має вигляд:

A =

1 -1 2 1 0

2 1 3 0 1

Базисні змінні – це змінні, які входять тільки в одне рівняння системи обмежень і при цьому з одиничним коефіцієнтом.

Економічний сенс додаткових змінних

Додаткові змінні задачі ЛП позначають надлишки сировини, часу та інших ресурсів, що залишаються у виробництві даного оптимального плану. Розв’яжемо систему рівнянь щодо базисних змінних x4​,x5​. Вважаючи, що вільні змінні дорівнюють 0, отримуємо перший опорний план:

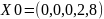
Базисне рішення називається допустимим, якщо воно невід’ємне.

Базис	B	x1	x2	x3	x4	x5
x4	2	1	-1	2	1	0
x5	8	2	1	3	0	1
F(X0)	0	1	1	-3	0	0

Переходимо до основного алгоритму симплекс-методу

Ітерація №0.

1. Перевірка критерію оптимальності. Поточний опорний план не є оптимальним, оскільки в індексному рядку знаходяться негативні коефіцієнти.

2. Визначення нової базисної змінної. Як ведучу виберемо стовпець, відповідний змінній x3​, оскільки це найбільший коефіцієнт за модулем.

3. Визначення нової вільної змінної. Визначимо значення Di​ по рядках як частка від ділення bi​/ai3​ і з них виберемо найменше:

Отже, 1-й рядок є ведучим.

Розв’язуючий елемент дорівнює 2 і знаходиться на перетині ведучого стовпця та ведучого рядка.

Базис	B	x1	x2	x3	x4	x5	min
x4	2	1	-1	2	1	0	1
x5	8	2	1	3	0	1	8/3
F(X1)	0	1	1	-3	0	0

4. Перерахунок симплексної таблиці. Формуємо наступну частину симплексної таблиці. Замість змінної x4​ в план 1 увійде змінна x3​. Рядок, що відповідає змінній x3​ в плані 1, отримана в результаті ділення всіх елементів рядка x4​ плану 0 на розв’язуючий елемент РЕ=2. На місці розв’язуючого елемента отримуємо 1. В інших клітинках стовпця x3​ записуємо нулі. Таким чином, в новому плані 1 заповнені рядок x3​ і стовпець x3​. Усі інші елементи нового плану 1, включаючи елементи індексного рядка, визначаються за правилом прямокутника.

B	x1	x2	x3	x4	x5
2 : 2	1 : 2	-1 : 2	2 : 2	1 : 2	0 : 2
8-(2*3):2	2-(1*3):2	1-(-1*3):2	3-(2*3):2	0-(1*3):2	1-(0*3):2
0-(2*-3):2	1-(1*-3):2	1-(-1*-3):2	-3-(2*-3):2	0-(1*-3):2	0-(0*-3):2

Отримуємо нову симплекс-таблицю:

Базис	B	x1	x2	x3	x4	x5
x3	1	1/2	-1/2	1	1/2	0
x5	5	1/2	5/2	0	-3/2	1
F(X1)	3	5/2	-1/2	0	3/2	0