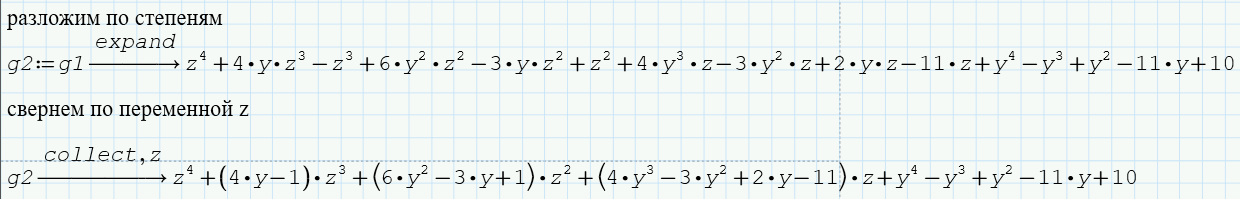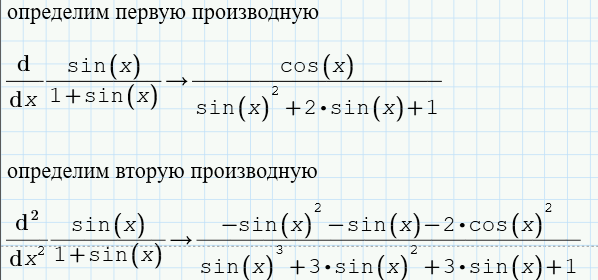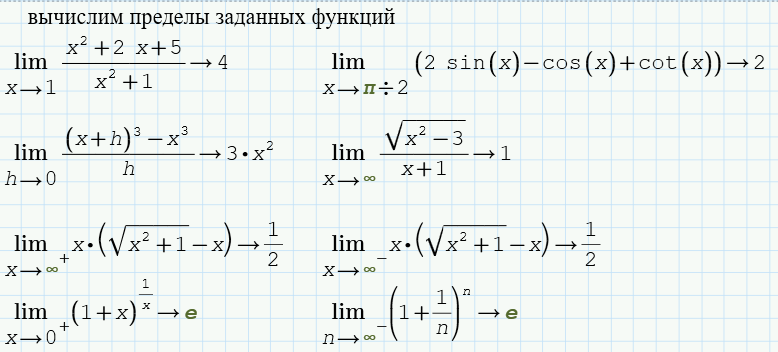Часть 3. Символьные вычисления
Упражнение 1.
Используя операцию float, представим заданные значения в требуемом формате.
Для применения указанной команды требуется объявить в рабочей области программы число, добавить float и отметить количество позиций, которое может занимать запись величины.
Пример обращения к оператору показан на рисунке 33.
|
Рисунок 33 – Вызов функции float |
Упражнение 2.
Выведем заданные числа в комплексной форме.
Для выполнения указанной задачи в приложении существует команда complex. Чтобы запись получилась более корректной, также воспользуемся операторами factor и float.
Полученные выражения представлены на рисунке 34.
|
Рисунок 34 – Преобразование комплексных чисел |
По условию задачи, требовалось реализовать упрощение последнего выражения. Выполнение данного действия также можно видеть на рисунке выше.
Упражнение 3.
Выполним преобразования заданного полинома g(x).
На рисунке 35 отображены результаты разложения выражения на множители и замены переменной, входящей в формулу. Отмеченные действия были реализованы с помощью операторов factor и explicit.
|
Рисунок 35 – Разложение выражения на множители и замена параметра |
На рисунке 36 приведены многочлены, сформированные путём использования функций expand, позволяющей разложить на степени выражение, и collect, реализующей сворачивание формулы по указанной переменной.
|
Рисунок 36 – Обращение к функциям expand и collect |
Упражнение 4.
Разложим выражения на элементарные дроби, используя операцию parfrac.
Исходные данные, записанные в расширенном виде, показаны на рисунке ниже.
|
Рисунок 37 – Преобразование в частичные доли |
Упражнение 5.
Представим заданные выражения в виде ряда составляющих с порядком разложения 6 элементов.
Ряд Тейлора можно сформировать с помощью функции series, после запятой также требуется отметить порядок разложения.
Полученные выражения представлены на рисунке 38.
|
Рисунок 38 – Разложение на составляющие |
Упражнение 6.
Для определения первообразной аналитически заданной функции f(x) воспользуемся инструментом «Интеграл», который помещен в раздел «Операторы».
Выведенное выражение можно изучить на рисунке 39.
|
Рисунок 39 – Применение команды «Интеграл» |
Упражнение 7.
Определим символьное
значение первой и второй производных
выражения f(x) с помощью специального
оператора «Производная», обозначенного
в программе в виде «
».
На рисунке 40 приведены формулы, полученные в ходе дифференцирования исходной функции.
|
Рисунок 40 – Использование оператора «Производная» |
Упражнение 8.
На рисунке 41 можно видеть результат выполнения трёх различных операций с заданными матрицами.
Транспонирование массива осуществляется путём обращения к одноименному оператору, который графически представляется в виде «МТ».
Инверсия матрицы совпадает по обозначению с возведением объекта в степень -1.
Вычислить детерминант элемента можно с помощью функции det().
|
Рисунок 41 – Матрицы в приложении Mathcad |
Упражнение 9.
Для вычисления пределов заданных функций обратимся к одноименному инструменту, расположенному в разделе программы «Символьные операции».
Результат произведенных действий отображен на рисунке 42.
|
Рисунок 42 – Вычисление пределов выражений |
Упражнение 10.
Осуществим создание пользовательских операторов путём прикрепления различных символов к заданным вычислительным процедурам.
Программная реализация математических модулей для перевода электрической энергии представлена на рисунке 43.
|
Рисунок 43 – Конвертация единиц электрической энергии |
Техническое исполнение математических модулей, выполняющих пересчет магнитной индукции, показано на рисунке 44.
|
Рисунок 44 – Конвертация единиц магнитной индукции |
Программная реализация математических модулей для перевода мощностных характеристик приведена на рисунке 45.
|
Рисунок 45 – Конвертация единиц мощности |
