МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ

Кафедра прикладной информатики

ОЦЕНКА

ПРЕПОДАВАТЕЛЬ

старший преподаватель _________________ А.В. Сорокин

подпись, дата

ЛАБОРАТОРНАЯ РАБОТА №2

Основы работы в системе Mathcad Вариант 19

по дисциплине «Моделирование»

РАБОТУ ВЫПОЛНИЛ

СТУДЕНТ ГР. Z9411 __________________ А.С. Чурилов

подпись, дата

Студенческий билет № 2019/3684

Санкт-Петербург 2023г.

Оглавление

Выполнение практических заданий 3

Часть 1. Основы работы с Mathcad 3

Часть 2. Решение уравнений средствами Mathcad 13

Часть 3. Символьные вычисления 18

Ответы на контрольные вопросы 25

Часть 1. Основы работы с Mathcad 25

Часть 2. Решение уравнений средствами Mathcad 29

Часть 3. Символьные вычисления 34

Заключение 37

Выполнение практических заданий Часть 1. Основы работы с Mathcad

Упражнение 1.

Вычислим в системе Mathcad значения заданных выражений. Для выполнения необходимых арифметических операций применим следующие команды: «Квадратный корень», «Модуль», «Факториал».

На рисунке 1 представлены найденные численные величины.

Рисунок 1 – Выполнение арифметических вычислений

Упражнение 2.

Определим заданные переменные a, b, c и выражения Z и N.

Локальное объявление выполняется с помощью комбинации знаков «:=», глобальное – путём применения оператора «≡».

После записи значений переменных добавим в документ выражения Z и N и найдём их величины. Стандартная точность отображения чисел – 3 знака в десятичной части.

Осуществление требуемых вычислений приведено на рисунке 2.

Рисунок 2 – Вычисление выражений в Mathcad

Изменим точность отображения значений до 4-ёх знаков после запятой. В результате реализации данного действия величины выражений Z и N представляются в программе более подробно, что демонстрируется на рисунке ниже.

Рисунок 3 – Произведение расчетов с заданной точностью

Упражнение 3.

Выведем на экран значение системной константы π со стандартной точностью отображения. После выполним повторную печать данной величины, установив максимальный формат ее представления локально.

Полученные значения показаны на рисунке 4.

Рисунок 4 – Локальное изменение точности отображения

Упражнение 4.

Выполним заданные операции с комплексными числами Z, Z₁ и Z₂.

На рисунке 5 представлено определение комплексного числа Z и применение к нему следующих операторов и функций: «Модуль», «Возврат вещественной части», «Возврат мнимой части», «Вычисление главного значения аргумента», «Квадратный корень», «Умножение».

Рисунок 5 – Вычисление выражений с одним комплексным числом

На рисунке 6 показано объявление комплексных чисел Z1 и Z2 и выполнение с ними следующий действий: «Сложение», «Вычитание», «Умножение», «Деление».

Рисунок 6 – Вычисление выражений с двумя комплексными числами

Упражнение 5.

Выполним ряд заданных операций различного вида.

Для вычисления суммы и произведения выражения, содержащего переменную-диапазон, в приложении Mathcad существуют специальные операторы, обозначаемые символами «∑» и «∏», соответственно.

На рисунке 7 представлено определение дискретного параметра и выполнение отмеченных действий.

Рисунок 7 – Нахождение суммы и произведения вектора

Вычисление определенных интегралов производится с помощью одноименного оператора. Также в системе есть возможность вывести выражение производной любого порядка и найти её значение в конкретной точке.

Реализация описанных действий приведена на рисунке 8.

Рисунок 8 – Вычисление определенных интегралов и значений производных в точке

Упражнение 6.

Определим в программе Mathcad векторы i, d, S и R, как показано на рисунке 9.

Рисунок 9 – Задание векторов

Отобразим графически функцию S_i(d_i). Для добавления чертежа перейдём в раздел «Графики» и воспользуемся функцией «Вставить график». Требуемый вид построения называется «График XY», а тип – «Линейная кривая».

Результат вставки графика в документ представлен на рисунке 10.

Рисунок 10 – Построение графика зависимости Si(di)

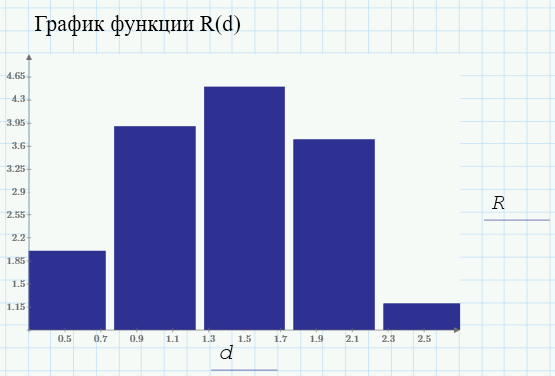
Отобразим зависимость, описываемую функцией R_i(d_i), в виде вертикальной гистограммы. Требуемый формат построения называется «График XY», а тип – «Кривая "столбцы"».

Результат вставки диаграммы в документ приведен на рисунке 11.

Рисунок 11 – Построение графика зависимости Ri(di)

Упражнение 7.

Построим декартовы и полярные графики заданных функций X(α), Y(α) и P(α).

Определим в приложении вектор α. Зададим выражения для функций X(α), Y(α) и P(α), тем самым сформировав соответствующие столбцы значений. Полученные одномерные матрицы показаны на рисунке 12.

Рисунок 12 – Задание векторов

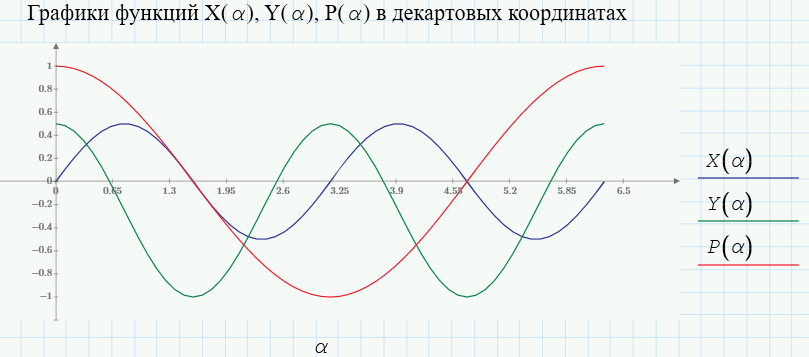
На рисунке 13 приведены графики функций X(α), Y(α) и P(α), построенные в одной декартовой плоскости. Данное действие реализовано с помощью применения функции «Добавить кривую».

Рисунок 13 – Нанесение графиков зависимостей X(α), Y(α), P(α) в декартовой плоскости

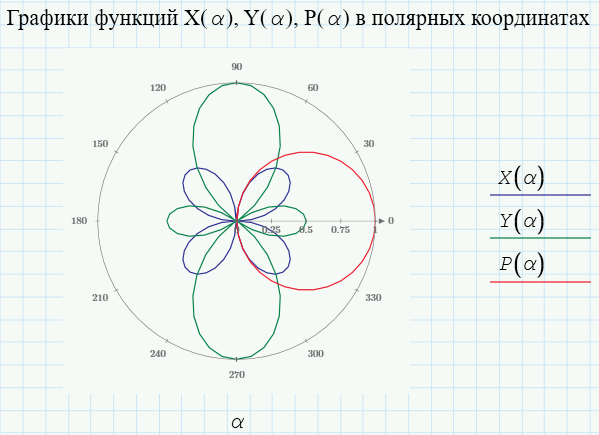
Представим кривые заданных зависимостей в полярных координатах. Для этого в разделе «Добавить график» требуется выбрать вид «Полярный график». Полученный чертеж отображен на рисунке 14.

Рисунок 14 – Нанесение графиков зависимостей X(α), Y(α), P(α) в полярных координатах

Определим координаты одной из точек пересечения графиков функций Y(α) и P(α). Воспользуемся встроенной возможностью программы добавления горизонтального и вертикального маркеров для поиска общих значений.

Результат реализации поставленной задачи приведен на рисунке 15.

Рисунок 15 – Применение маркеров на графике

Вычислим значения функций X(α) и Y(α) в точке α=π/2. Математические выкладки можно видеть на рисунке 16.

Рисунок 16 – Определение значений функций в точке

Упражнение 8.

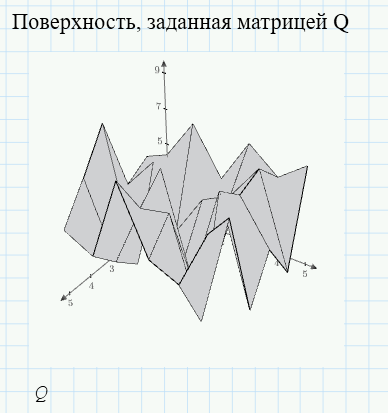
Создадим матрицу Q размером 6×6 и заполним ее произвольными значениями. Сформированный двумерный массив представлен на рисунке 17.

Рисунок 17 – Создание и заполнение матрицы

Во вкладке «Вставить график» выберем команду «3D-график». На рисунке 18 отображена поверхность, построенная по значениям элементов массива Q.

Рисунок 18 – Задание 3D-фигуры с помощью матрицы

Упражнение 9.

Построим график поверхности и карту линий уровня для заданной функции двух переменных различными способами.

Сформируем 3D-фигуру с помощью применения инструкции CreateMesh(). Пример использования указанного метода представлен на рисунке ниже.

В качестве второго способа обратимся к математическому заданию поверхности. На рисунке 19 также демонстрируется результат подобного варианта построения чертежа.

Рисунок 19 – Создание поверхности двумя разными методами

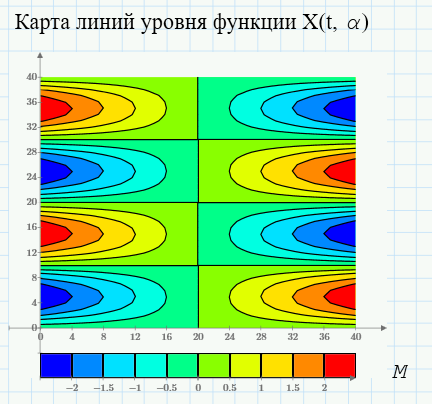
Карта линий уровня поверхности задаётся путём использования команды «Вставить график», где в качестве вида чертежа выбирается пункт «Контурный график».

Карта линий уровня для функции двух переменных отображена на рисунке 20.

Рисунок 20 – Контурный график функции

Упражнение 10.

Отобразим графически пересечение двух поверхностей, заданных функциями.

Определим матрицы для построения поверхностей с помощью оператора CreateMesh(). Образованный чертеж показан на рисунке 21.

Рисунок 21 – Построение поверхностей A и B, определенных функциями f1(x,y) и f2(x,y)

Упражнение 11.

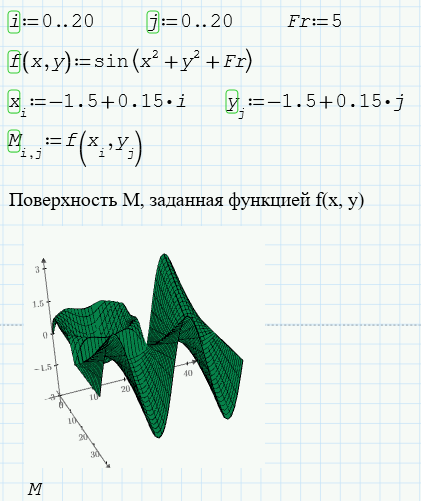
Выполним построение поверхности, соответствующей требованиям индивидуального задания:

• переменные и функции:

i := 0..20; j := 0..20; Fr := 5 (значение выбрано самостоятельно из заданного диапазона);

f(x,y) := sin(x² + y² + Fr);

x_i := -1.5+0.15*i; y_j := -1.5+0.15*j;

M_i,j := f(x_i, y_j).

• тип графика:

график поверхности, в месте для ввода матрицы указать М.

Объявим исходные параметры i, j и Fr. Также определим функцию f(x, y) и зададим значения векторов x_i и y_j.

Поверхность, построенная по значениям матрицы M, элементы которой были найдены на основе равенства M_i,j := f(x_i, y_j), приведена на рисунке 22.

Рисунок 22 – Построение заданной поверхности