МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»
ИНСТИТУТ НЕПРЕРЫВНОГО И ДИСТАНЦИОННОГО ОБРАЗОВАНИЯ
Кафедра прикладной информатики
ОЦЕНКА
ПРЕПОДАВАТЕЛЬ
старший преподаватель _________________ А.В. Сорокин
подпись, дата
ЛАБОРАТОРНАЯ РАБОТА №4
Исследование датчиков равномерно распределенных псевдослучайных чисел Вариант 19
по дисциплине «Моделирование»
РАБОТУ ВЫПОЛНИЛ
СТУДЕНТ ГР. Z9411 __________________ А.С. Чурилов
подпись, дата
Студенческий билет № 2019/3684
Санкт-Петербург 2022г.
Оглавление
Цель работы 3
Описание исследуемого алгоритма 4
Изучение работы мультипликативного датчика 7
Моделирование последовательности СВ при N=100 7
Моделирование последовательности СВ при N=600 8
Моделирование последовательности СВ при N=1000 10
Сравнение качества работы датчика с выборками разной длины 12
Ответы на контрольные вопросы 14
Заключение 17
Приложение 18
Цель работы
Цель лабораторной работы: ознакомление с методами и алгоритмами моделирования случайных событий в программной среде MATLAB, а также изучение тестов для проверки качества моделирования.
Описание исследуемого алгоритма
В настоящей работе выполняется исследование алгоритма получения на ПК псевдослучайных последовательностей, равномерно распределенных на интервале от 0 до 1. Подобные программы называются генераторами равномерно распределенных чисел.
На данный момент разработано множество методов построения генераторов. Одним из наиболее простых механизмов моделирования псевдослучайных чисел можно назвать мультипликативный датчик.
Мультипликативный датчик – устройство, использующее для моделирования случайной величины, заданной в соответствии с равномерным законом, следующий алгоритм:
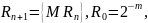
где m - число двоичных разрядов в мантиссе ячейки, М - достаточно большое целое число, {.} - взятие дробной части числа, заключенного в фигурные скобки. Рекомендуется М выбирать равным: 52p+1, где р - целое. На практике в качестве R0 часто задают случайное число из интервала (0,1).
Реализуем алгоритм, описанный формулой, на языке программирования MATLAB:
for i=1:N
R(i) = rem((M*R1),1);
R1 = R(i);
end
Для соблюдения свойства рекуррентности поместим основное выражение в рамки итерационного цикла for, значения в котором будут изменяться от 1 до N (длина выборки случайной величины) с шагом 1 (принимается системой по умолчанию).
В записи формулы для вычисления очередного элемента массива используется функция rem(), служащая для получения дробной части от переданного в качестве параметра значения.
Проверить качество моделируемого датчика можно с помощью нескольких тестов. Одним из таковых является вычисление критерия согласия Колмогорова-Смирнова. Он предназначен для анализирования простых гипотез о принадлежности исследуемой выборки некоторому полностью известному закону распределения.
Адаптируем критерий для настоящей работы, то есть применим к псевдослучайной последовательности, распределенной по равномерному закону. Формула примет следующий вид:
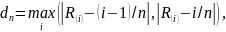
где {R(i)} = (R(1), R(2), … R(n)) – вариационный ряд, построенный по выборке Rn = {Ri} = (R1, R2, … Rn).
В среде MATLAB величину критерия согласия можно вычислить с помощью следующих программных инструкций:
for i=1:N
A(i) = abs(RR(i)-(i-1)/N);
B(i) = abs(RR(i)-i/N);
end
for i=1:N
D(i)=max(A(i),B(i));
end
Dn = max(D);
В приведенном фрагменте используются две циклические конструкции for от 1 до N. В первом вычисляются значения векторов А и В. В выражениях, предназначенных для этого, применяется функция abs(). Во второй же структуре выбирается максимальный элемент среди пары членов с одинаковыми индексами из двух данных массивов, за счет чего формируется новая последовательность D. Результирующая величина – наибольшее значение вектора D. Выполнение описанного действия возможно благодаря встроенной команде max().
Уточнить качество используемого датчика также можно путём определения вероятности равномерности образованной выборки. Данный параметр вычисляется по формуле:
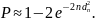
Запишем отмеченное выражение в приложении MATLAB:
P = 1-2*exp(-2*N*(Dn^2));
Как видно, в формуле для нахождения вероятности применены стандартные математические операторы такие, как: умножение «*», вычитание «-» и возведение в степень «^».
В изучении смоделированного распределения воспользуемся визуальной составляющей, предоставляемой функционалом системы MATLAB. С помощью команд hist(), plot() и ecdf() запросим вывод на экран гистограммы случайной величины, линейного графика её распределения и кривой эмпирической функции распределения.
Полный текст разработанной программы моделирования мультипликативного датчика можно изучить в разделе «Приложение» настоящего отчета.