17. Теоретические распределения случайных величин и их свойства: биномиальное распределение, распределение Пуассона, нормальное распределение.

Распределение Бернулли (определить вероятность успешного исхода при одном испытании.)

Биномиальное распределение (определения вероятности появления определенного числа успешных исходов при n независимых испытаниях)

Распределение Пуассона (описывает число событий, происходящих в одинаковых промежутках времени или на одинаковых площадях, при условии, что события происходят независимо друг от друга.)

Биномиальное распределение и распределение Пуассона для случайной величины Х можно рассчитать по таблицам.

К непрерывным распределениям относят нормальное, а также связан-ные с нормальным распределения: Стьюдента, – сигма^2 квадрат и F – распределение Фишера.

18. Коэффициенты асимметрии и эксцесса.

19. Коэффициент асимметрии и эксцесса - это меры, используемые в статистике для измерения формы распределения вероятностей случайной величины.

    Коэффициент асимметрии измеряет степень и направление асимметрии распределения случайной величины. Если распределение смещено вправо (больше значений сосредоточено слева от среднего), то коэффициент асимметрии положителен. Если распределение смещено влево (больше значений сосредоточено справа от среднего), то коэффициент асимметрии отрицателен. Для симметричных распределений коэффициент асимметрии равен нулю.

    Коэффициент эксцесса измеряет степень остроты или плоскости пика распределения случайной величины, а также наличие "тяжелых" хвостов. Положительный указывает на более острый и высокий пик, чем у нормального распределения (нормальное распределение имеет коэффициент эксцесса равный 0). Отрицательный коэффициент эксцесса указывает на более плоский пик, чем у нормального распределения.

    Средние величины: средняя арифметическая, взвешенная средняя, геометрическая средняя.

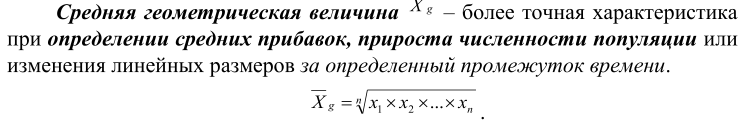
20. Меры разброса единиц совокупности: дисперсия и стандартное отклонение. Коэффициент вариации.

Дисперсия — мера варьирования числовых значений признака вокруг их средней арифметической, она измеряет и внутреннюю изменчивость значений признака, зависящую от разностей между наблюдениями.

Индекс х у s обозначает, что этот показатель хар варьирование числовых значений признака Х вокруг их средней величины.

!Чем менее однородна совокупность, тем большее значение будет иметь дисперсия.

Коэффициент вариации — среднее квадратическое отклонение, выраженное в процентах от величины средней арифметической.

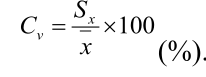
Ва-рьирование считается слабым, если не превосходит 10%, средним, когда Cv составляет 11-25%, и значительным при Cv>25%.

Коэффициент вариации является относительной мерой рассеяния при-знака и практически применяется в основном для сравнения выборок из од-нотипных генеральных совокупностей.

!!!!есть если Cv меньше или равен 0,333 – вариация считает слабой, а если больше 0,333 – сильной.