Производные переменные: пропорции, индексы.
Признаки (переменные) могут быть производными—вычисляемыми по какой-либо формуле.
Численность альтернатив можно выразить в долях единицы, а также в процентах от их общего числа n.
Доля (отношение, пропорция) – это отношение числа вариант, обладающих учитываемым признаком, к общему числу всех вариант. Доля обозначается через wd, а доля противоположной группы – qd
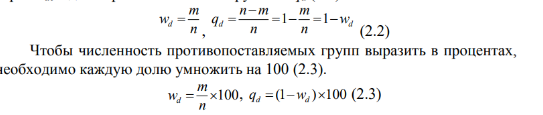
Индексы, которые, как и доля, являются относительными величинами. Индекс часто используют как показатель, получающийся в результате сравнения двух величин, характеризующих уровень изучаемого явления для двух разных периодов.
Индекс может быть выражен в виде коэффициентов или в виде процентов. Если индекс больше 1, уровень изучаемого явления растет, если меньше 1 – снижается.
С помощью индекса рассчитывается, например, индекс массы тела (ИМТ) – масса, скорректированная на рост.
Сплошное и выборочное обследование совокупностей.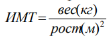
В зависимости от величины генеральной совокупности и целей исследования могут быть использованы методы сплошного или выборочного обследования.
Метод сплошного обследования включается в опросе всех потребителей генеральной совокупности на рынке. связан с высокими затратами на проведение исследования, его использование оправданно в случае малого количества потребителей, представляющих сегмент, или в случае больших размеров потребителя, когда объем покупок клиентов данного сегмента составляет значительную долю от емкости рынка в целом.
Метод выборочного обследования обеспечивает меньшую точность, однако он менее трудоемок. Целесообразно использование данного метода при наличии на рынке большого числа однородных потребителей.
Важность случайного (рендомизированного) отбора единиц наблюдения при формировании выборок.Случайный отбор единиц наблюдения — ключевой метод при формировании выборок в исследованиях, обеспечивает репрезентативность выборки и позволяет делать обобщения на всю популяцию.
1. помогает избежать смещения выборки, когда определенные группы или типы единиц наблюдения представлены в выборке недостаточно или, наоборот, слишком сильно. Это позволяет получить более объективные результаты и делать обобщения на всю популяцию.
2. обеспечивает статистическую значимость результатов и позволяет проводить статистические тесты для проверки гипотез. Это важно для того, чтобы убедиться, что различия или связи, выявленные в выборке, не случайны.
3. делает процесс формирования выборки более объективным и исключает субъективное вмешательство и предвзятость со стороны исследователя.
4.правильно выполненный случайный отбор обеспечивает репрезентативность выборки, то есть выборка точно отражает разнообразие и характеристики популяции, на которую делаются выводы.
5. можно обобщать результаты исследования на всю популяцию с большей уверенностью, так как выборка будет более точным представлением популяции.
Понятие о репрезентативной и смещенной выборках.
(Выборка должна быть репрезентативной (достигается способом рандомизации или случайным отбором вариант из генеральной совокупности.) Если выборка не является репрезентативной—смещенной.)
Репрезентативная выборка — это такая выборка, которая точно отражает структуру и характеристики генеральной совокупности. В репрезентативной выборке пропорции различных групп объектов сохраняются так же, как в генеральной совокупности. Это позволяет делать обобщения о всей совокупности на основе результатов выборки.
Смещенная выборка — это выборка, в которой присутствует систематическое отклонение от репрезентативности. Например, если выборка содержит слишком много объектов из одной группы или исключает другие группы, это может привести к смещению результатов. Смещенная выборка может давать недостоверные выводы о генеральной совокупности.
Важно стремиться к репрезентативной выборке, чтобы результаты исследования были надежными и обобщаемыми на всю совокупность.