53. Статистическая значимость регрессии. Проверка нулевой гипотезы о равенстве коэффициента регрессии нулю.

Для оценки качества подбора линейной функции к выборочным данным проводится дисперсионный анализ, и оценка значимости полученного урав-нения регрессии дается с помощью F-критерия Фишера. В основе проверки значимости регрессии лежит идея разложения общей дисперсии результа-тивного признака на факторную и остаточную дисперсии, т.е. объясненную (за счет независимых факторов) часть дисперсии и часть, оставшуюся необъ-ясненной в рамках данной модели. Предварительно рассчитываются девиаты, степени свободы, а потом и соответствующие дисперсии. Гипотезы такие же, как в случае проверки достоверности коэффициента регрессии, а выво-ды различаются.

Гипотезы:

Н0: в генеральной совокупности коэффициент регрессии равен нулю, признак-фактор не влияет на признак-результат.

Н1: в генеральной совокупности коэффициент регрессии не равен нулю, признак-фактор влияет на признак-результат.

Общая девиата, ответственная за общую изменчивость признака-результата.

Факторная девиата, ответственная за изменчивость признака-результата под действием признака-фактора.

Остаточная девиата, ответственная за изменчивость признака-результата под действием других факторов, исключая признак-фактор. Чем она меньше , тем лучше уравнение регрессии подходит к исходным данным. С помощью F-критерия определяют значимость всего уравнения регрессии.

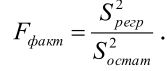
Вывод: если фактически установленная величина Fфакт больше Fst. для степеней свободы регрессии и остатков на принятом уровне значимости β, нулевую гипотезу отвергают. Иначе нулевую гипотезу отвергнуть нельзя.

54. Стандартные ошибки параметров регрессионного уравнения.

Гипотезы:

Н0: в генеральной совокупности коэффициент регрессии равен нулю, признак-фактор не влияет на признак-результат.

Н1: в генеральной совокупности коэффициент регрессии не равен нулю, признак-фактор влияет на признак-результат.

Вывод: если фактически установленная величина tфакт – отношения вы-борочного коэффициента регрессии к своей ошибке больше tst для чисел степеней свободы k = n – 2 на принятом уровне значимости, нулевую гипотезу отвергают. Иначе нулевую гипотезу отвергнуть нельзя

55. Коэффициент детерминации. Анализ остатков. Оценка величины остаточной дисперсии.

56. Коэффициент детерминации используется для измерения того, насколько хорошо модель регрессии соответствует данным.

    • доля общей изменчивости зависимой переменной, которая объясняется регрессионной моделью.

    • R-квадрат принимает значения от 0 до 1, где 1 означает идеальное соответствие модели данным.

    Анализ остатков включает в себя оценку остатков, которые представляют разницу между фактическими значениями зависимой переменной и значениями, предсказанными моделью. Путем анализа остатков можно проверить предпосылки регрессионной модели, такие как нормальность распределения остатков, отсутствие автокорреляции и гетероскедастичности.

    Оценка величины остаточной дисперсии позволяет определить степень изменчивости остатков вокруг регрессионной линии. Это важно для проверки однородности дисперсии остатков. Если остаточная дисперсия не постоянна, это может указывать на наличие однородности дисперсионных остатков, что может привести к неправильным выводам из модели (с помощью F-критерия)

    Нахождение доверительной области для линии регрессии.

57. • можно воспользоваться методом доверительных интервалов для параметров регрессии.

    Доверительная область для линии регрессии показывает, где с некоторой вероятностью (обычно 95%) находится истинная линия регрессии.

    Для этого можно построить доверительные интервалы для коэффициентов наклона и свободного члена линии регрессии. используя эти интервалы, можно построить доверительную область вокруг линии регрессии.

    Общий подход к нахождению доверительной области для линии регрессии включает следующие шаги:

    1. Оценка коэффициентов наклона и свободного члена линии регрессии с помощью метода наименьших квадратов.

    2. Построение доверительных интервалов для оценок коэффициентов наклона и свободного члена с учетом стандартной ошибки и выбранного уровня доверия.

    3. Использование этих доверительных интервалов для построения доверительной области вокруг линии регрессии.

    Построение доверительной области позволяет учитывать неопределенность, связанную с оценкой коэффициентов регрессии, и предоставляет информацию о том, где с высокой вероятностью находится истинная линия регрессии.

    Понятие о нелинейной и множественной регрессионной зависимости.

Нелинейная регрессионная зависимость означает, что связь между зависимой переменной и одной или несколькими независимыми переменными не может быть описана простой линейной моделью. Вместо этого используются более сложные функции, такие как квадратичные, экспоненциальные, логарифмические и другие. Например, если данные показывают криволинейную зависимость, то модель может быть аппроксимирована квадратичной функцией вместо линейной.

Множественная регрессионная зависимость возникает, когда зависимая переменная связана с двумя или более независимыми переменными.

Нельзя просто суммировать влияние нескольких факторов, необходимо учитывать и влияние независимых факторов друг на друга. При этом каждый фактор влияет на результат, через связь с другими факторами. – метод множественной регрессии.

Коэффициента регрессии в уравнении множественной регрессии показывает как в среднем изменится значение результативного признака, если соответствующий факторный признак увеличится на единицу при фиксированных значениях всех остальных факторов.