Частная и множественная корреляции.
Частная корреляция – это связь между двумя признаками (результативным и факторным или между двумя факторными) при фиксированном значении других факторных признаков.
Множественная корреляция – это связь между результативным и двумя или более факторными признаками, включенными в исследование.
Коэффициент ранговой корреляции Спирмена.
Если варианты исследуемых признаков не распределяются по нормальному закону (или если распределение неизвестно), а также для признаков, измеренных в порядковой шкале, для определения связи между признаками используют непараметрические показатели.
Гипотезы:
Н0: в генеральной совокупности коэффициент корреляции Спирмена равен нулю, связь между изучаемыми признаками отсутствует. 1
Н1: в генеральной совокупности коэффициент корреляции Спирмена не равен нулю, есть связь между изучаемыми признаками.
Алгоритм проведения теста:
1. признаки по отдельности ранжируют по возрастанию.
2. Каждой варианте каждого признака присваивается свой ранг Одинаковым по величине вариантам присваивается один и тот же средний ранг.
3. Проверяют суммы рангов каждого признака, они должны получиться равными.
4. Находят разность между рангами для каждой пары вариант признаков X и Y.
5. Проверяют сумму разности рангов, она должна быть равной 0.
6. Рассчитывают квадрат разности между рангами для каждой пары ва-риант.
7. Находят сумму квадратов разностей.
8. Рассчитывают коэффициент корреляции Спирмена по формуле
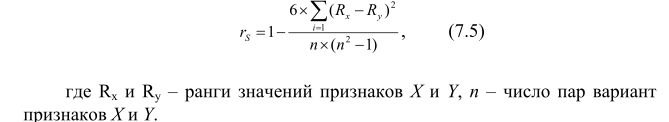
9. Значимость коэффициента корреляции рангов оценивают с помощью коэффициента Стьюдента как для выборочного коэффициента корреляции.
Вывод: если фактически установленная величина tфакт – отношения вы-борочного коэффициента корреляции к своей ошибке – больше tst. для чисел степеней свободы k = n – 2 на принятом уровне значимости β, нулевую гипо-тезу отвергают. Иначе нулевую гипотезу отвергнуть нельзя.
может принимать значения от –1 до +1.
Назначение регрессионного анализа.
Основная цель регрессионного анализа состоит в том, чтобы определить взаимосвязь между переменными, характер и силу воздействия переменных и сделать прогнозы на основе модели.
Регрессионное уравнение и его показатели.
Регрессиомнный анализ (линейный) – статистический метод исследо-вания зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1, X2, ..., Xm описывается уравнением общего вида:
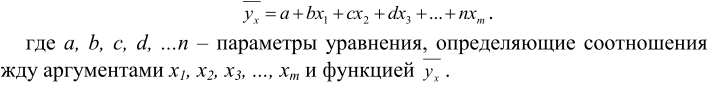
Связь коэффициента регрессии с коэффициентом корреляции.
Регрессионный анализ нельзя использовать для определения наличия связи между переменными, поскольку наличие такой связи и есть предпосылка для применения анализа.
Для выборки уравнения имеют вид:
Регрессионный и корреляционный анализы часто рассматривают совместно
После того, как исследователь убедится в наличии статистически значимых связей между анализируемыми переменными с помощью корреляционного анализа, он приступает к выявлению и математическому описанию конкретного вида зависимостей между ними: подбирает класс аппроксимирующих функций, производит отбор наиболее информативных предикторов (независимых переменных), вычисляет оценки неизвестных параметров уравнения, анализирует – полученной модели. Все это и составляет содержание регрессионного анализа.
Основная задача регрессионного анализа – установление математического вида связи между одной переменной (называемой зависимой переменной) и несколькими другими (называемых независимыми переменными).
Оценка параметров регрессионного уравнения по выборке с помощью метода наименьших квадратов.
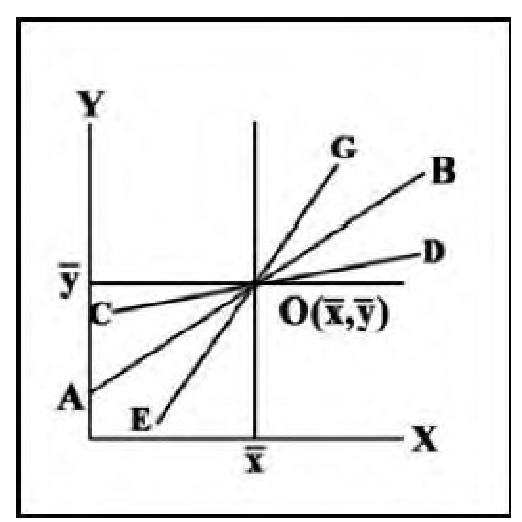
Оценки генеральных параметров коэффициентов уравнения получают с помощью метода наименьших квадратов (МНК), который позволяет рассчитать такие выборочные коэффициенты а и b, при которых сумма квадратов отклонений фактических (наблюдаемых) значений результативного признака от расчетных (предсказанных регрессией) минимальна. (из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой ли-
нией была бы минимальной, и проходила бы через точку О( x , y ), соответствующую средним обеих переменных)
