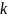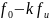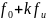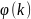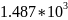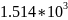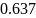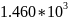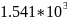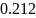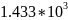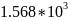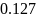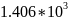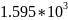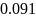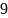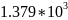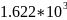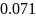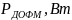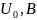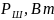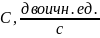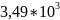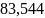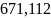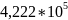- •«Московский Технический Университет Связи и Информатики»
- •«Общая Теория Связи (отс)»
- •Исходные данные варианта №6.
- •Назначение отдельных элементов схемы.
- •Временные диаграммы.
- •Полагая, что последовательность дискретных отсчётов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования:
- •Рассматривая отклик квантователя как случаный дискетный сигнал с независимыми значения на входе l – ичного дискретного канала связи (дкс)
- •Закодировать значения l – ичного дискретного сигнала двоичным блочным примитивным кодом, выписать все кодовые комбинации кода и построить таблицу кодовых расстояний кода:
- •Полагая, что для передачи икм сигнала по непрерывному каналу связи (нкс) используется гармонический переносчик:
- •С учётом заданного вида приёма (детектирования) сигнала дискретной модуляции:
- •Рассматривая отклик декодера пру как случайный дискретный сигнал на выходе l – ичного дкс:
- •Полагая фнч на выходе цап приёмника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения:
- •Список используемой литературы.
Полагая, что для передачи икм сигнала по непрерывному каналу связи (нкс) используется гармонический переносчик:
а) Рассчитать нормированный к амплитуде переносчика, спектр модулированного сигнала и его начального ширину спектра.
Расчёт нормированного к амплитуде переносчика, спектр модулированного сигнала и его начальная ширина спектра производился по формулам ниже. Данные перенесены в таблицу 7.1.
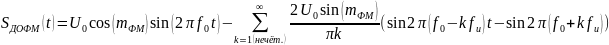 (27)
(27)
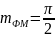 (28)
(28)
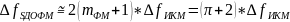 (29)
(29)
– Спектральное разложение ДОФМ сигнала;
– Индекс фазовой модуляции (макс. Отклонение фазы сигнала ДОФМ от несущей фазы);
– Формула расчёта ширины спектра сигнала ДОФМ.
Спектральное разложение ДОФМ сигнала представлено ниже, в таблице 7.1.
Таблица 7.1. – Спектральное разложения ДОФМ сигнала.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ширина спектра, полученная в результате
расчёта, составляет
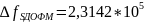
б) Построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нём найденную ширину спектра.
График нормированного спектра сигнала дискретной модуляции показан на рисунке 7.1.
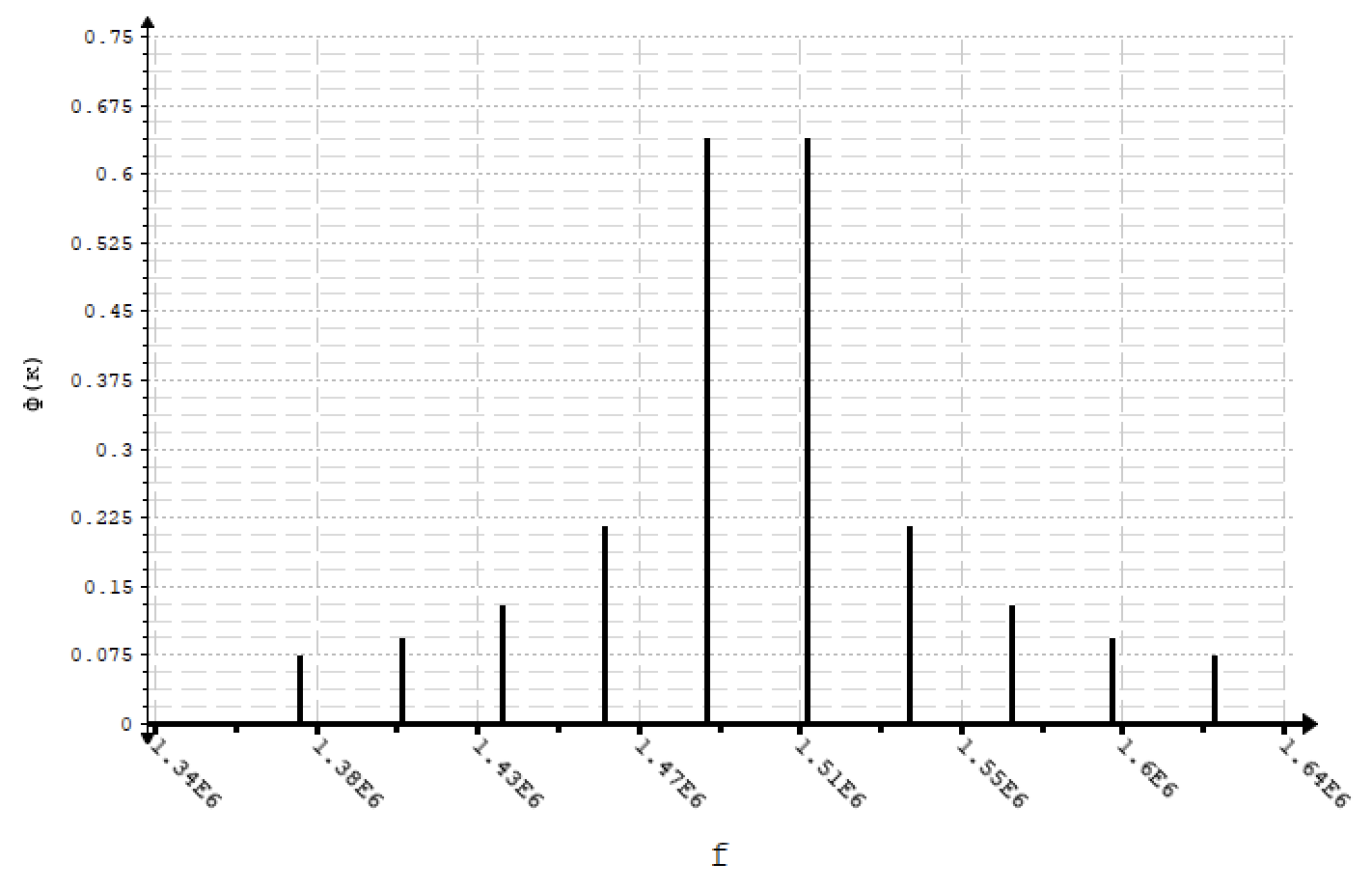


Рисунок 7.1. – Спектр дискретной модуляции.
Рассматривая НКС, как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношением сигнал/шум:
а) Рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС.
Расчёт мощности сигнала ДОФМ, амплитуды модулированного сигнала, дисперсии (мощности) аддитивной помехи в полосе частот сигнала и пропускной способности НКС произведён нижеперечисленным формулам. Данные перенесены в таблицу 8.1.
 (30)
(30)
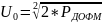 (31)
(31)
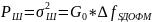 (32)
(32)
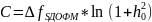 (33)
(33)
– Формула расчёта мощности сигнала ДОФМ;
– Формула расчёта амплитуды модулированного сигнала;
– Формула расчёта дисперсии (мощности) аддитивного шума;
– Формула расчёта пропускной способности НКС.
Таблица 8.1. – Данные мощности сигнала ДОФМ, амплитуды модулированного сигнала, дисперсии (мощности) аддитивной помехи в полосе частот сигнала и пропускной способности НКС.
б) Построить в масштабе четыре графика функций плотности вероятностей (ФПВ) мгновенных значений и огибающих узкополосной Гауссовской помехи (УГП) и суммы гармонического сигнала УГП.
Необходимые ФПВ представлены ниже. Графики данных ФПВ представлены на рисунках с 8.1 по 8.4 соответственно. На рисунке 8.5 показаны графики 8.1 и 8.3 на одной плоскости, а на рисунке 8.6 показаны графики 8.2 и 8.4 на одной плоскости.
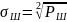 (34)
(34)
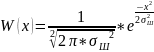 (35)
(35)
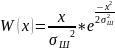 (36)
(36)
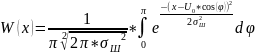 (37)
(37)
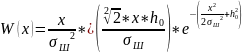 (38)
(38)
– Формула расчёта корня дисперсии (мощности) шума;
– ФПВ;
– Ф-ция огибающей Гауссовской помехи, распределённая по закону Релея;
– ФПВ аддитивной смеси гармонического сигнала и узкополосной Гауссовской помехи;
– ФПВ, огибающей принимаемого сигнала, подчинённой обобщ. распределению Релея (расп. Райса).
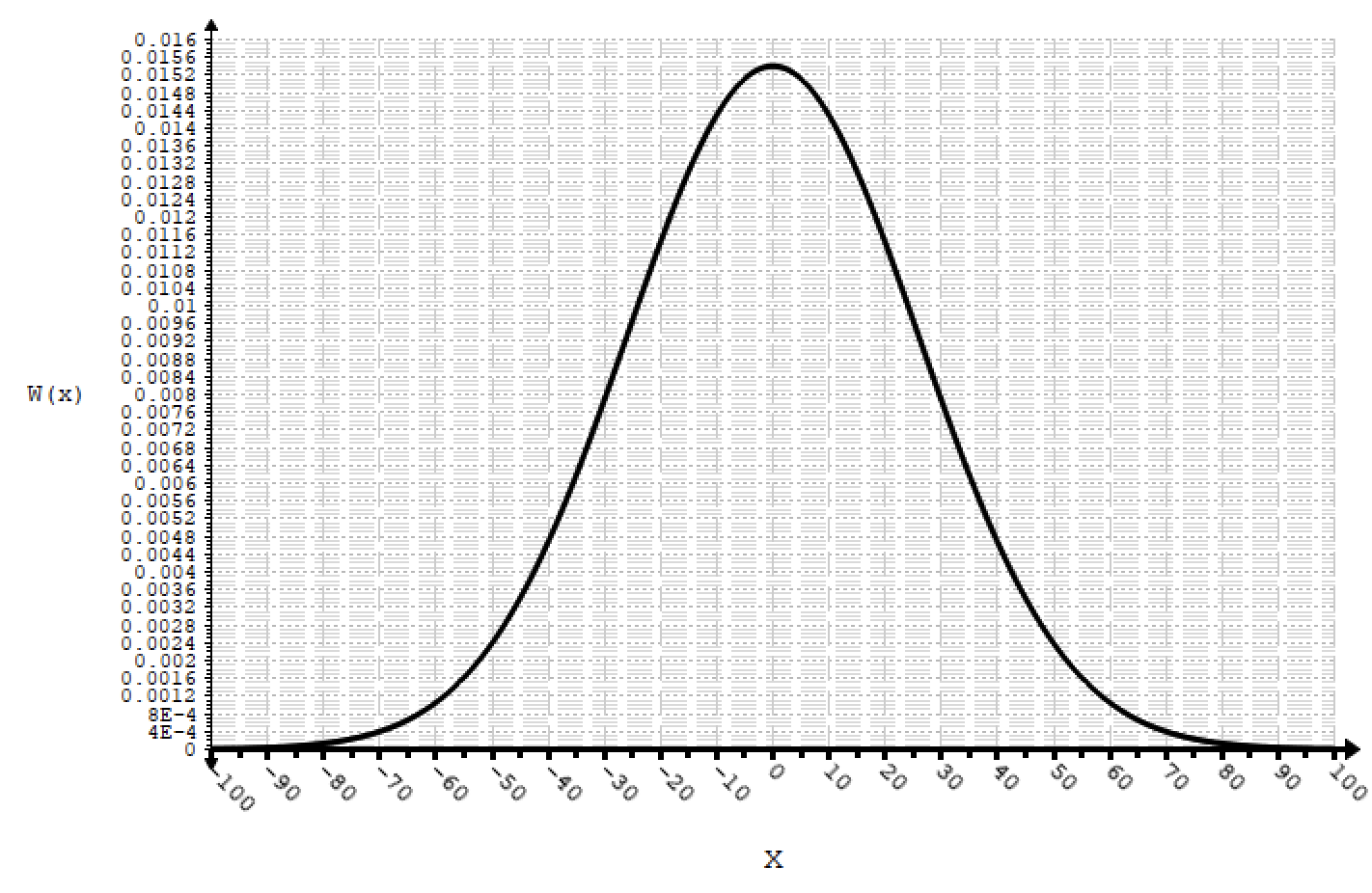
Рисунок 8.1. – ФПВ.
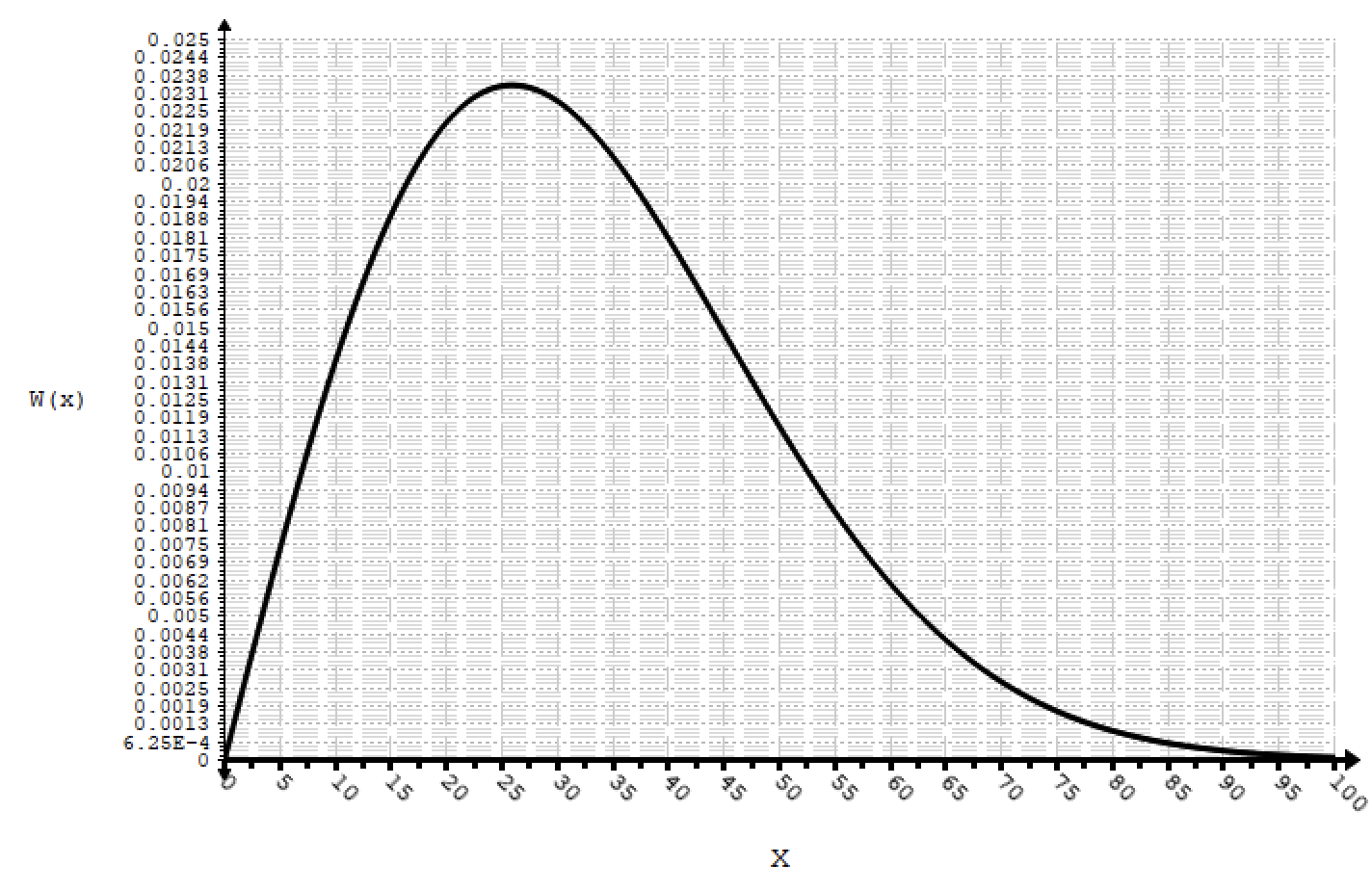
Рисунок 8.2. – Функция огибающей Гауссовской помехи, расп. По з-ну Релея.
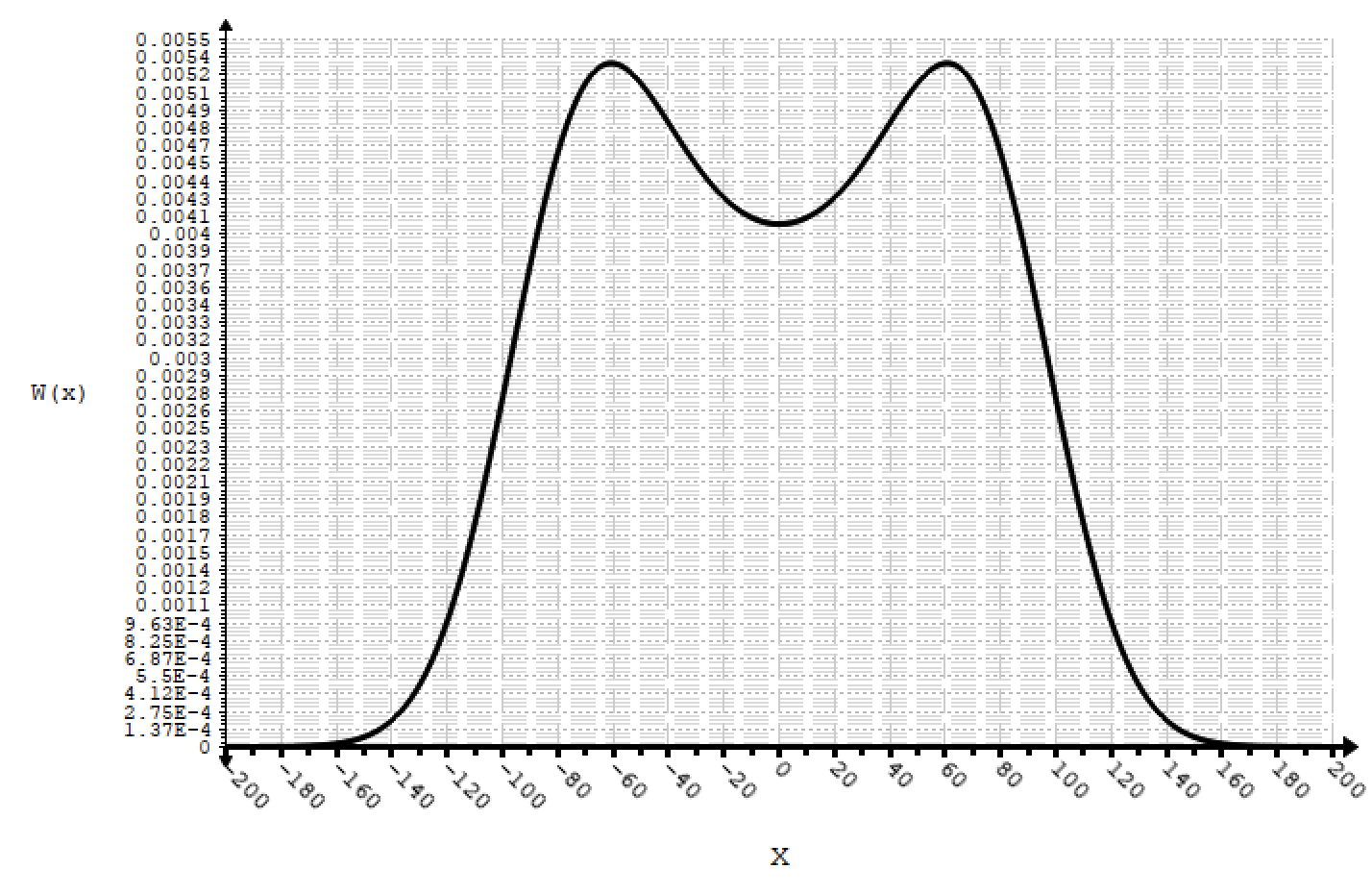
Рисунок 8.3. – ФПВ аддитивной смеси гармонического сигнала и узкополосной Гауссовской помехи.
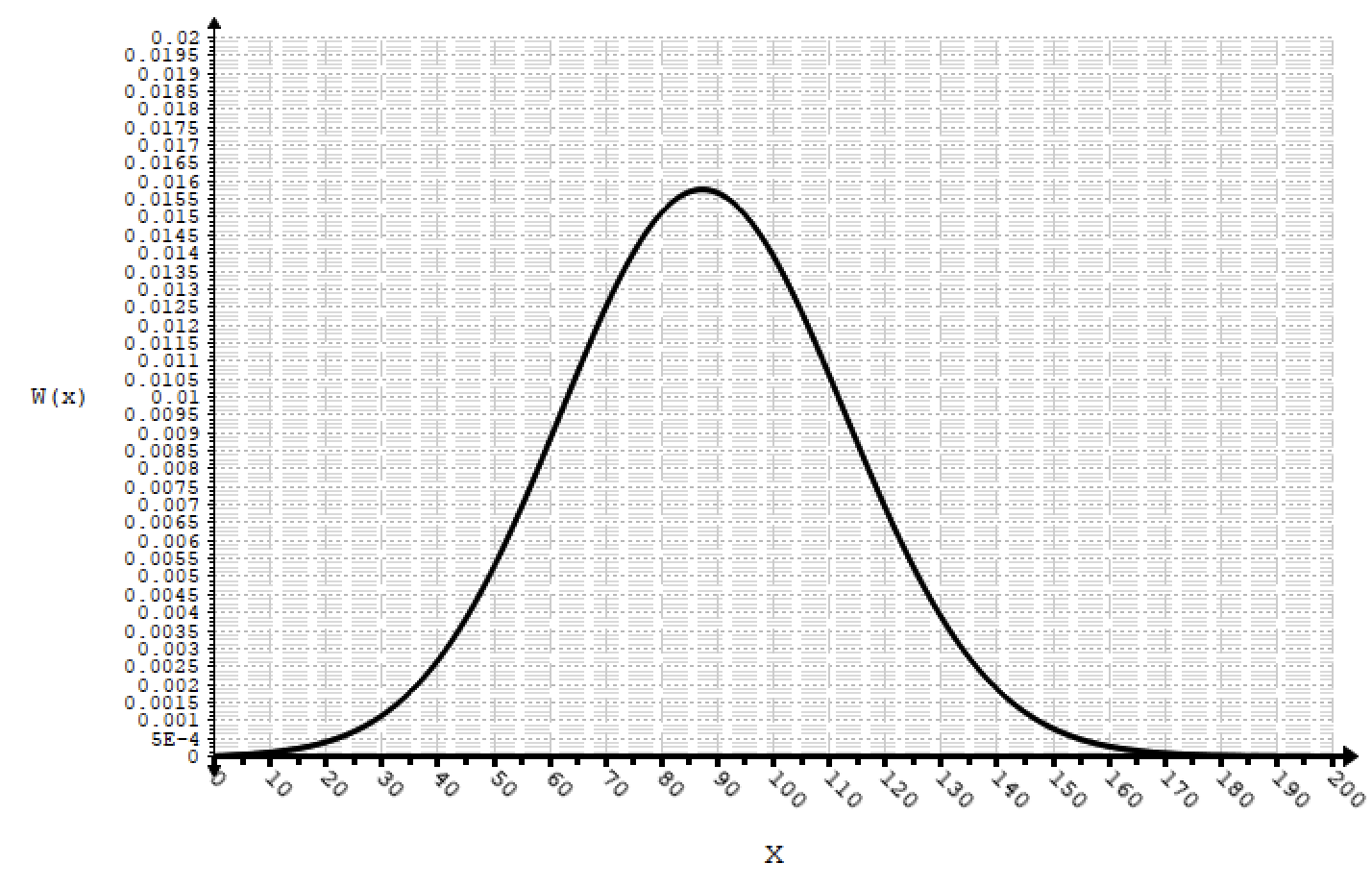
Рисунок 8.4. – ФПВ, огибающей принимаемого сигнала, подчинённой обобщ. распределению Релея (расп. Райса).
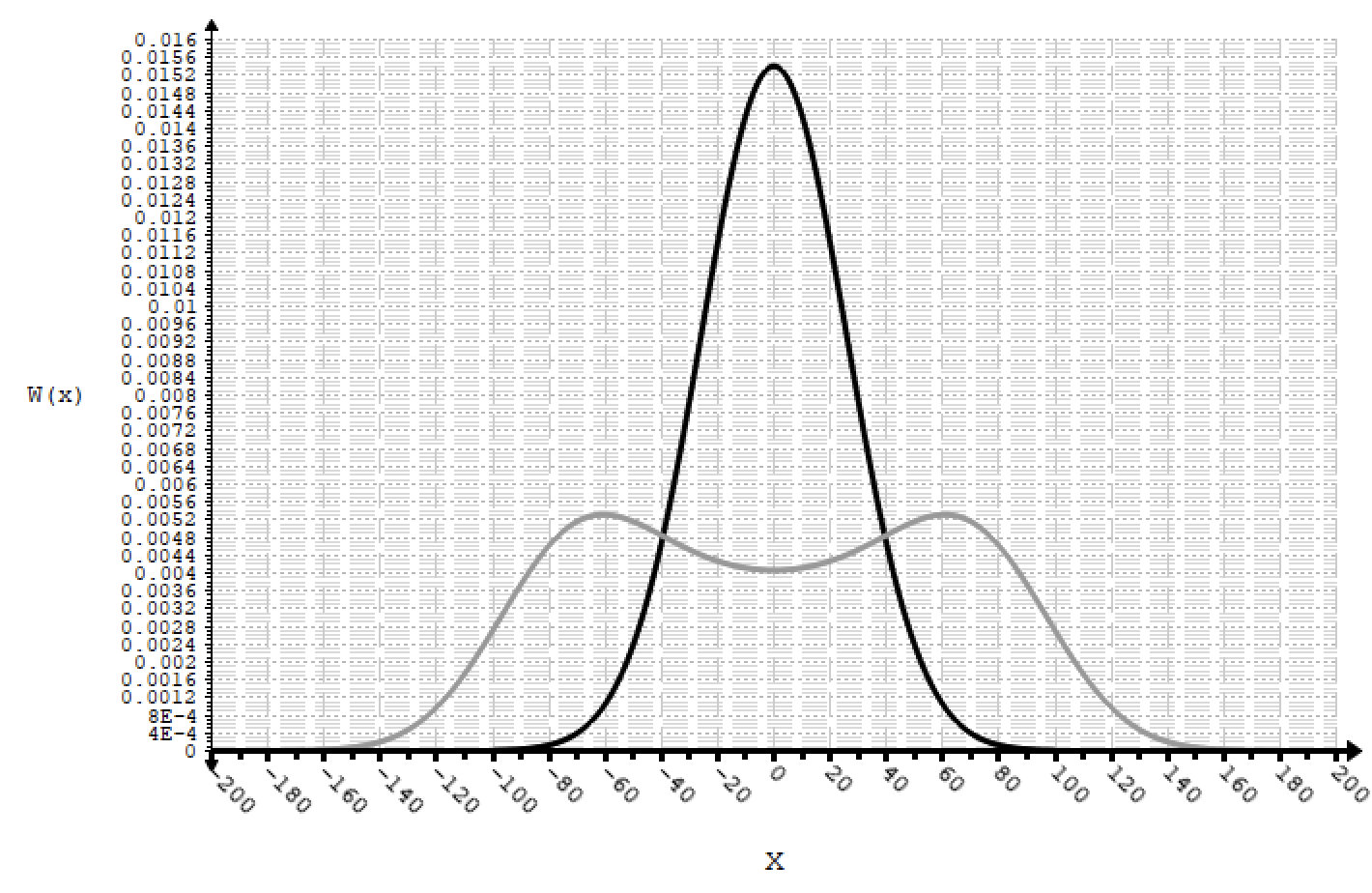
Рисунок 8.5. – Графики 8.1 и 8.3 на одной плоскости.
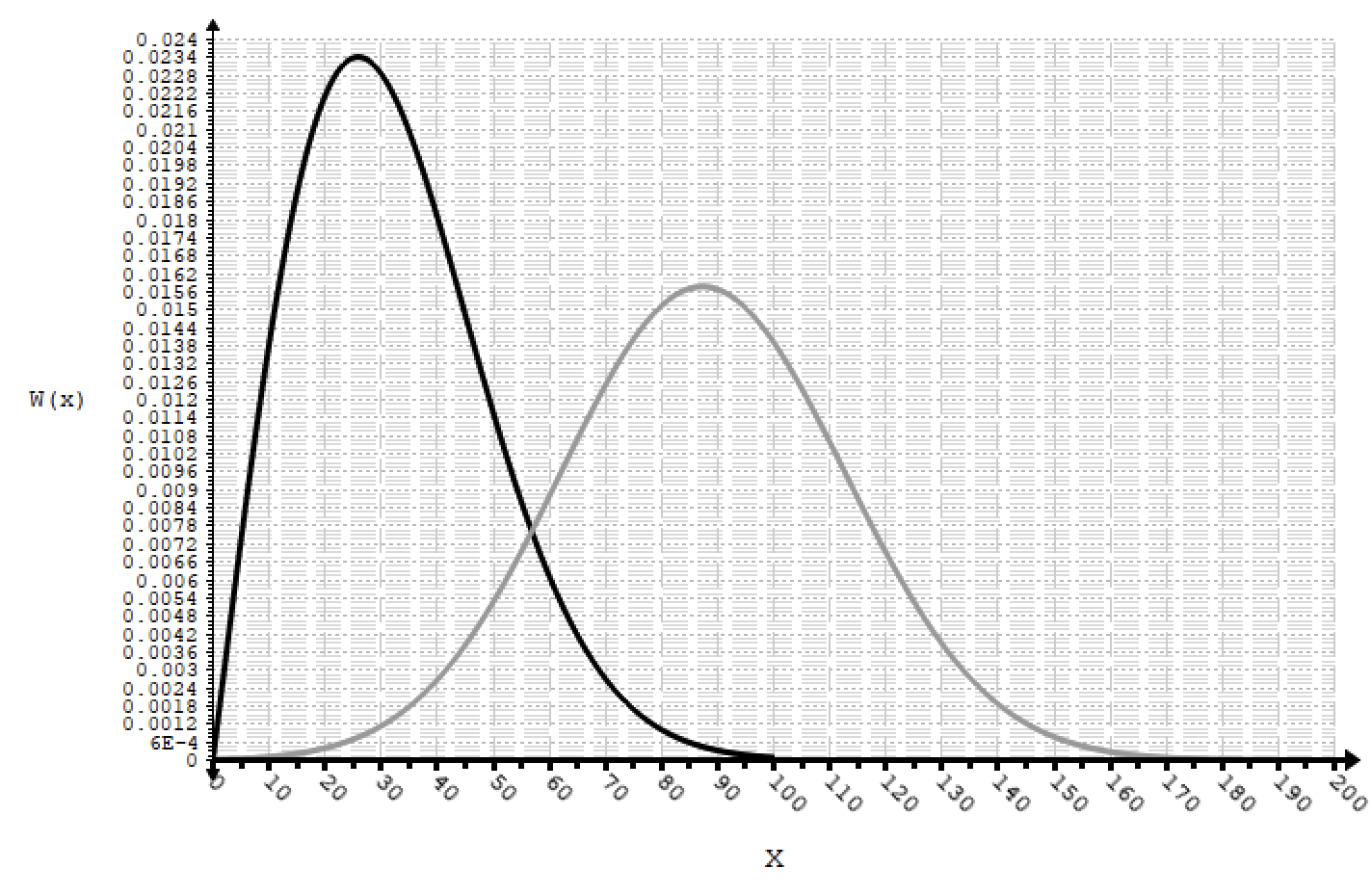
Рисунок 8.6. – Графики 8.2 и 8.4 на одной плоскости.