
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И
МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский Технический Университет Связи и Информатики»
Кафедра «Общей Теории Связи»
Лабораторная работа №26.2
«Анализ рекурсивных Цифровых Фильтров 1-го и 2-го порядка»
по дисциплине
«Цифровая Обработка Сигналов»
Выполнил студент гр. XXXX:
https://t.me/mattervisualizer, Вариант №6
Проверил: проф. каф. Общей Теории Связи
Поборчая. Н. Е.
Москва, 2023 г.
Содержание.
Цель работы.
На персональном компьютере провести экспериментальный анализ рекурсивных фильтров (ЦФ) первого и второго порядков. Исследовать частотные и временные характеристики фильтров, а также их взаимосвязь со значениями коэффициентов (параметров) ЦФ. Определить области устойчивости рекурсивных фильтров первого и второго порядков.
Выполнение домашнего задания.
Исходные данные варианта №6 представлены в таблице 1.
Таблица 1. – Значения параметров фильтра.
-
Номер варианта
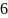

 .0
.0


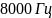
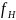



Разностное уравнение рекурсивного ЦФ первого порядка имеет вид:
 (1)
(1)
Подставив свои значения:
 (2)
(2)
Фильтр
является фильтром первого порядка,
поскольку максимальный коэффициент
параметра
 .
.
С труктурная
схема рекурсивного ЦФ первого порядка
представлена на рисунке 1.
труктурная
схема рекурсивного ЦФ первого порядка
представлена на рисунке 1.
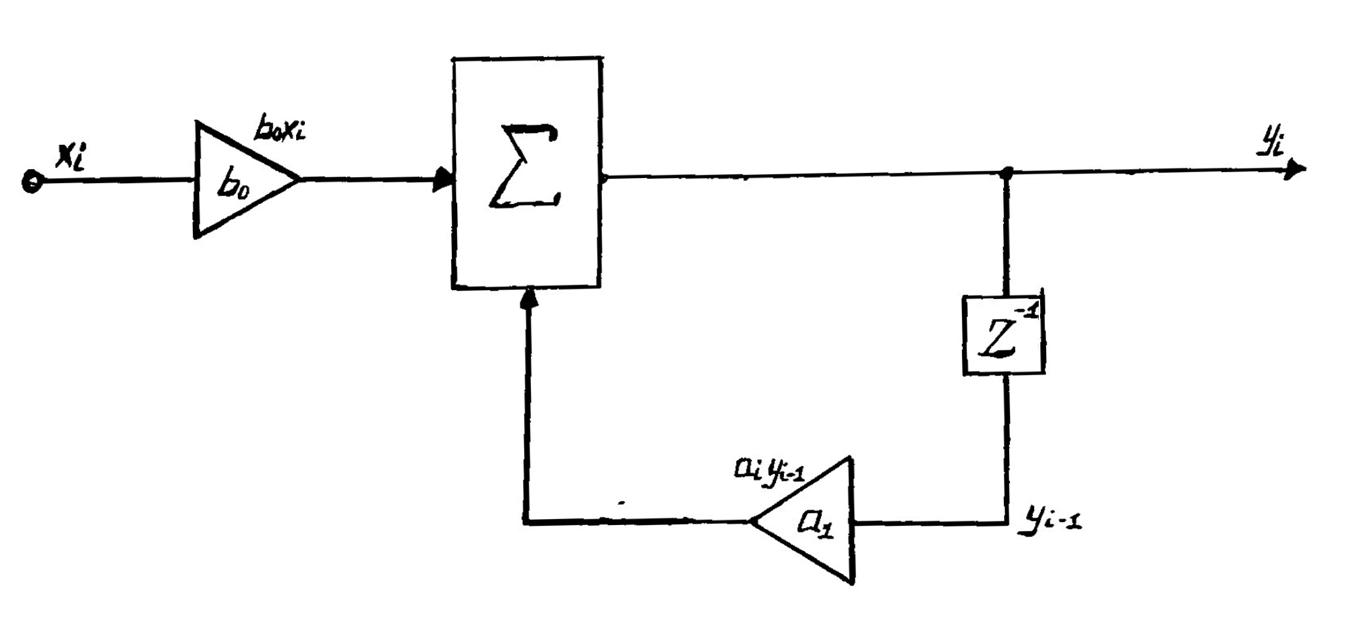
Рисунок 1. – Структурная схема рекурсивного ЦФ первого порядка.
Системной функцией ЦФ называется следующее отношения:
![]() (3)
(3)
Обе части были представлены с использованием Z-Преобразований:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
Следовательно:
![]() (8)
(8)
Следовательно:
![]() (9)
(9)
 (10)
(10)
Подставив значения получено:
![]() (11)
(11)
Импульсная
характеристика (ИХ) выражается следующим
образом, где
 – ИХ.
– ИХ.
![]() (12)
(12)
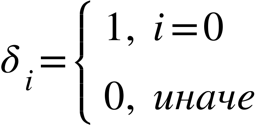 (13)
(13)
Импульсная характеристика была выражена следующим образом:
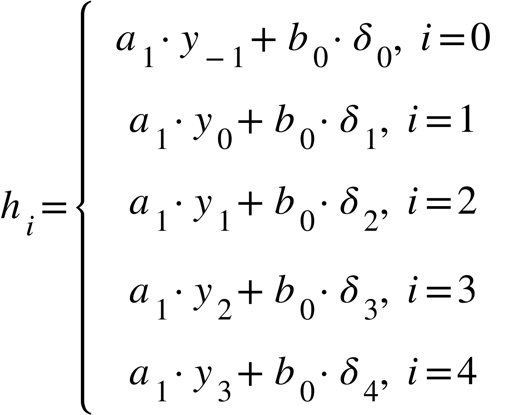 (14)
(14)
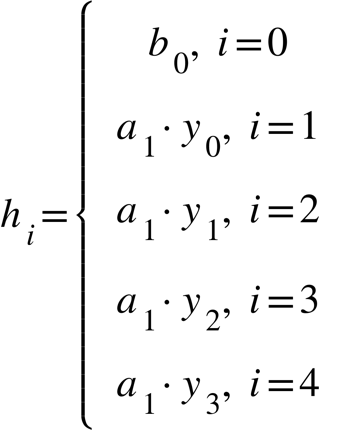 (15)
(15)
Следовательно:
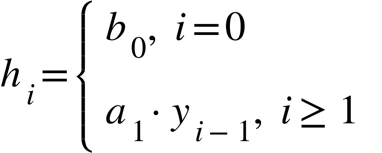 (16)
(16)
Подставив значения:
 (17)
(17)
График ИХ представлен на рисунке 2.

Рисунок 2. – График ИХ (импульсной характеристики).
Переходная характеристика была выражена следующим образом:
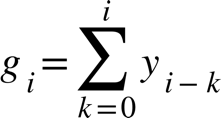 (18)
(18)
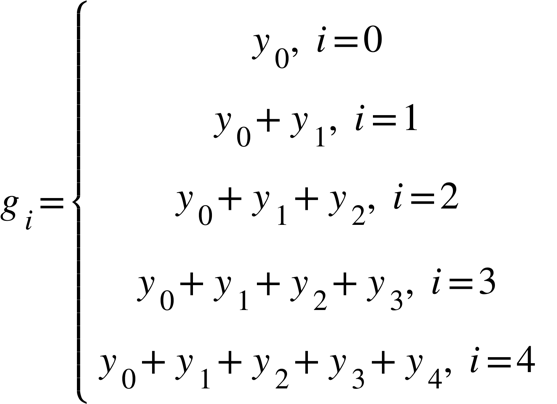 (19)
(19)
Следовательно:
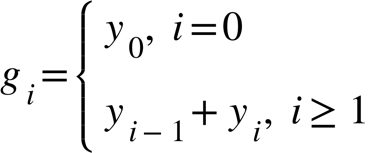 (20)
(20)
График ПХ представлен на рисунке 3.
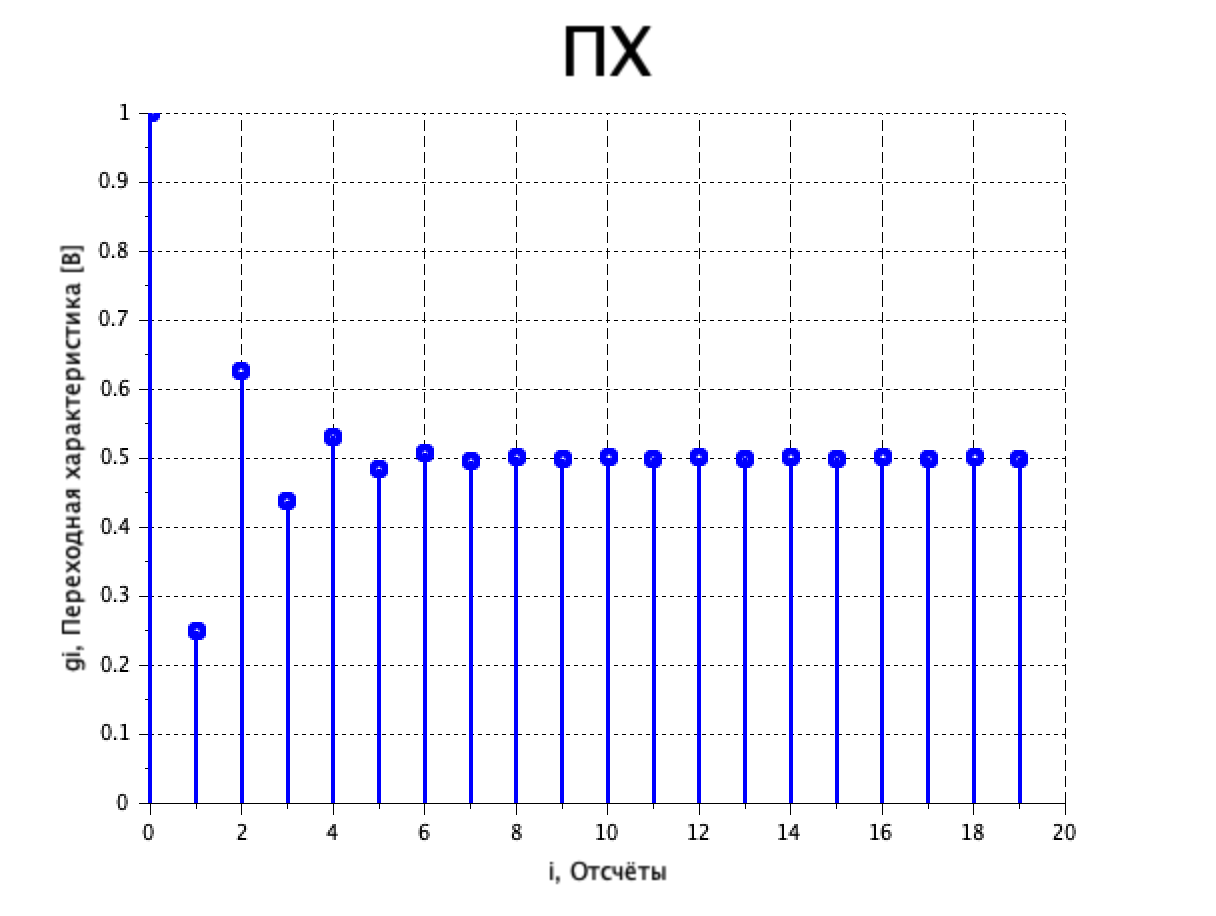
Рисунок 3. – График ПХ (импульсной характеристики).
Расчёт
АЧХ и ФЧХ производится с помощью ранее
найденной системной функции ЦФ. Заменив
в ней параметр
 на
на
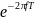 получаем:
получаем:
![]() (21)
(21)
По формуле Эйлера:
![]() (22)
(22)
Выделив действительную и мнимую часть, получаем:
![]() (23)
(23)
![]() (24)
(24)
![]()
![]() (25)
(25)
Следуя из всего написанного выше, формула АЧХ:
![]() (26)
(26)
Подставив значения:
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
![]() (30)
(30)
Следуя из всего написанного выше, формула ФЧХ:
![]() (31)
(31)
Подставив значения:
![]() (32)
(32)
График АЧХ представлен на рисунке 4.
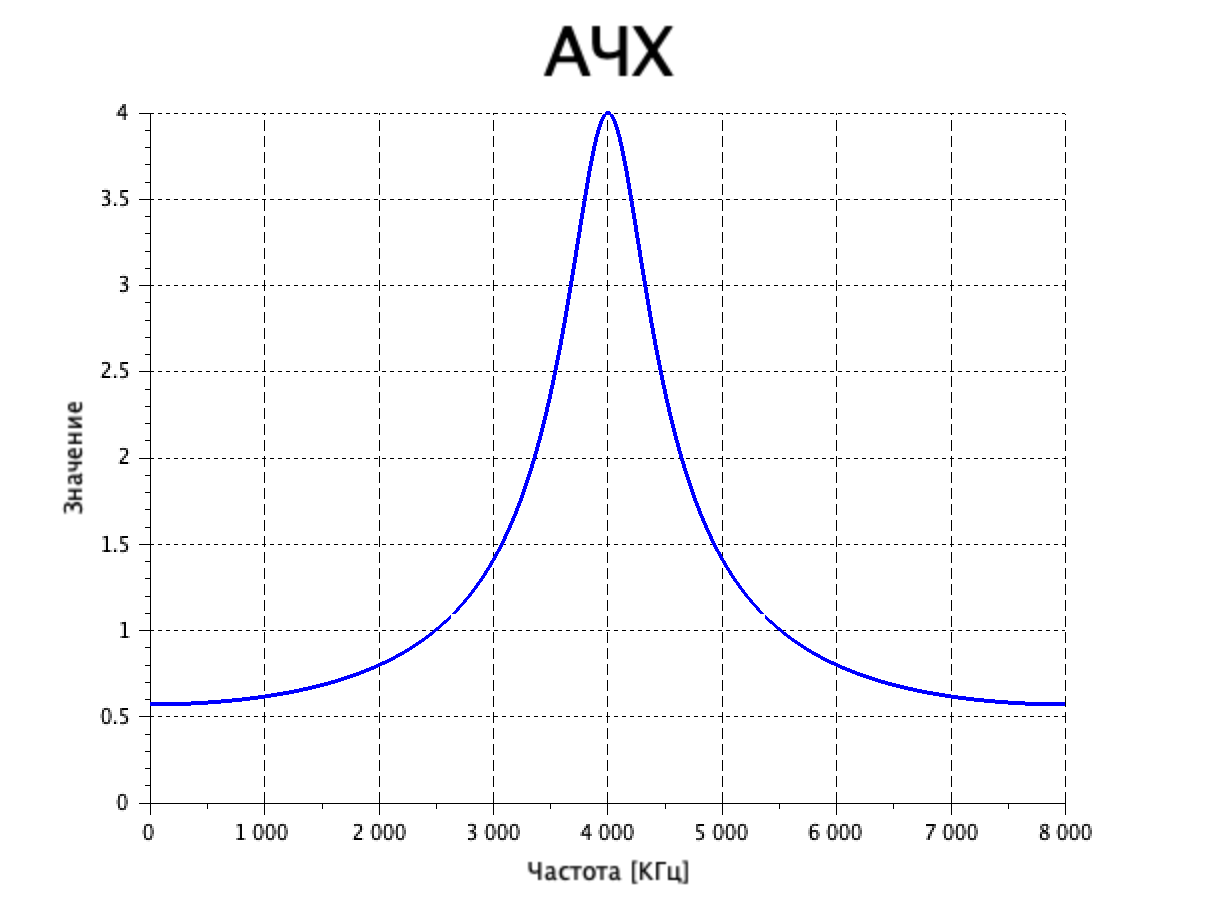


Рисунок 4. – График АЧХ.
График ФЧХ представлен на рисунке 5.
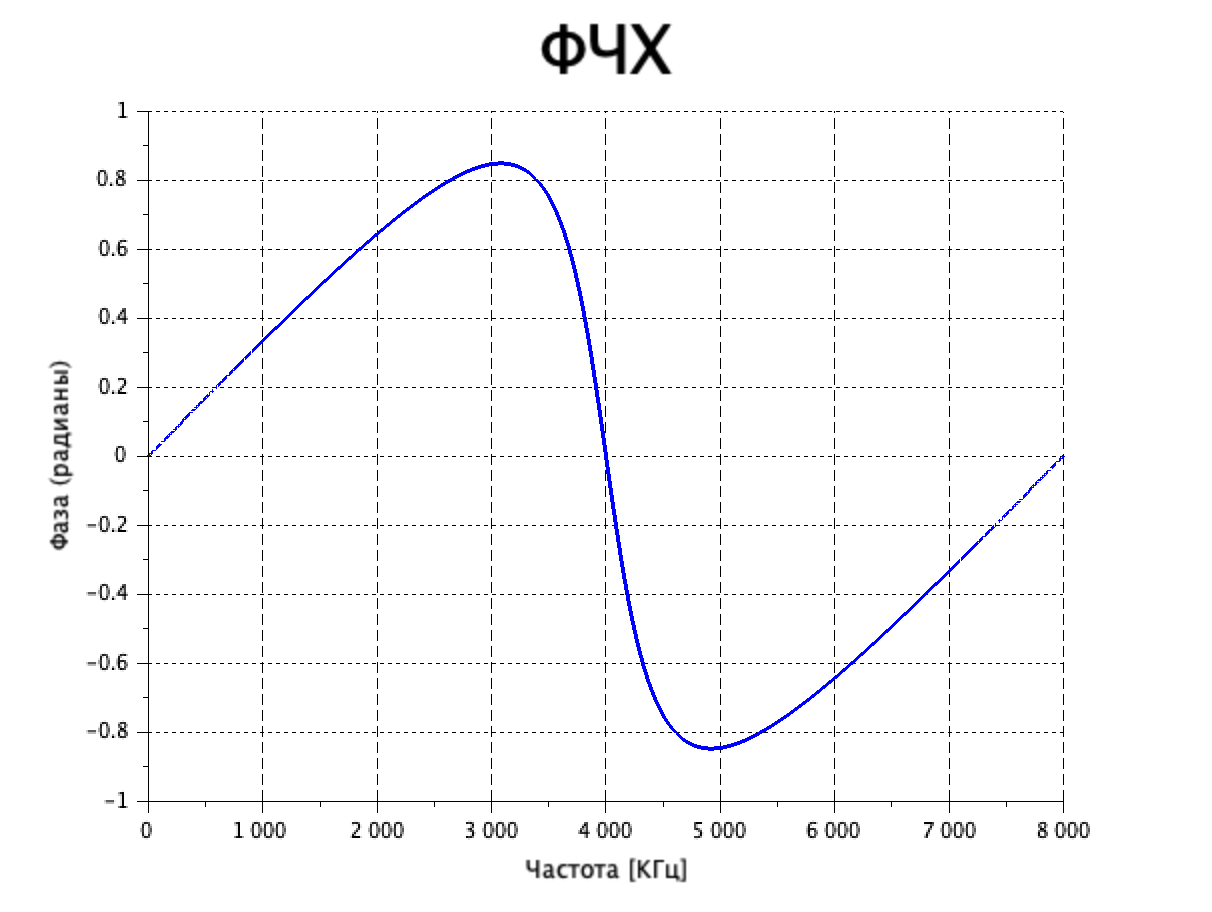

Рисунок 5. – График ФЧХ.
