ДДЗ отчет 6 вар

Министерство цифрового развития, связи и массовых коммуникаций Российской Федерации

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

СВЯЗИ И ИНФОРМАТИКИ

(МТУСИ)

Факультет "Радио и телевидение"

Кафедра "Теория вероятностей и прикладная математика"

Долгосрочное домашнее задание

по дисциплине "Теория вероятности и математическая статистика"

Вариант 06.

Выполнили

Проверил ______________________ Панков К.Н.

Москва 2024

1. Описательная статистика.

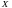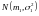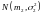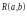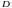Случайные величины и распределены по нормальному закону и соответственно. Случайная величина имеет равномерное распределение . Случайная величина – дискретна и имеет распределение Пуассона.

1. Выдвижение предположений

Будем полагать, что v061 и v064 соответствуют случайным величинам X и Y, которые распределены по нормальному закону, потому что в данных массивах выделяется среднее значение (для выборки v061 это примерно 2.63, а для v064 это примерно 0.9), которое встречается чаще всего и чем сильнее элементы выборки отличаются от этого среднего, тем реже они встречается.

Посмотрев выборки, можно сделать предположение, что v063 соответствует равномерному распределению случайной величины Z, такое предположение можно сделать, потому что все значения находятся в границах интервала [0; 5] и встречаются примерно одинаковое количество раз.

Выборка v062 соответствует распределению Пуассона, так как она обладает наибольшим коэффициентом асимметрии, и ее гистограмма асимметрична.

2. Анализ гистограмм частот

Число карманов: 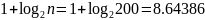. Число карманов будет равно 9.

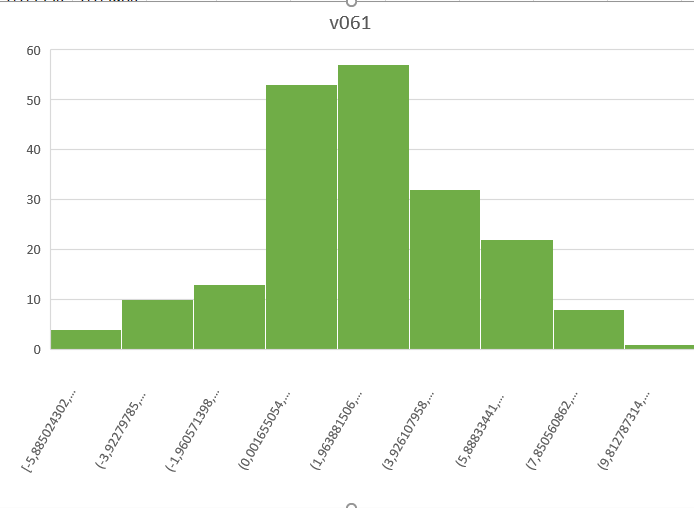
Рисунок 1 – Гистограмма частот для выборки v061

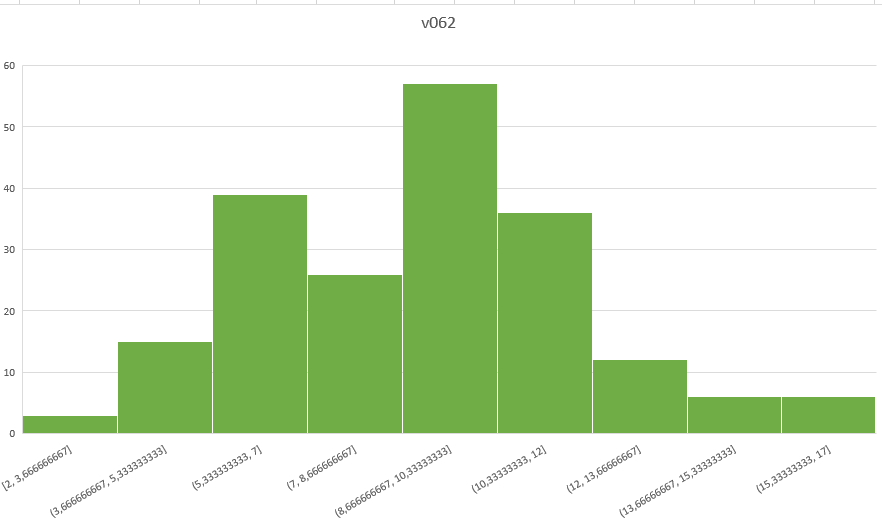
Рисунок 2 – Гистограмма выборки v062

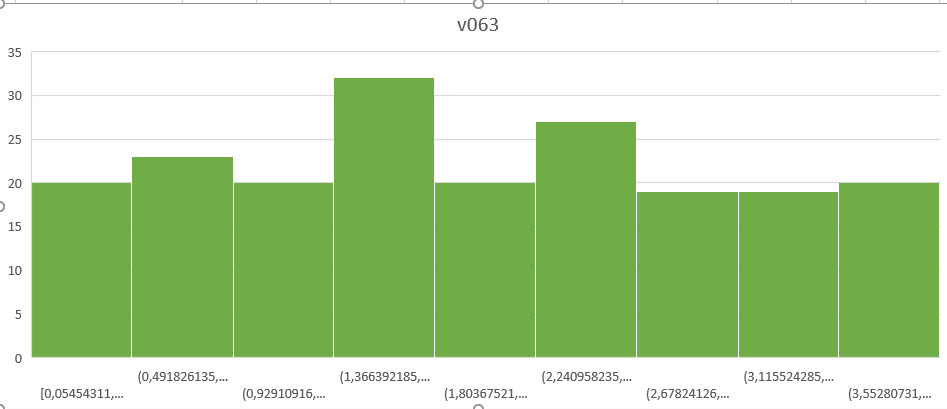
Рисунок 3 – Гистограмма выборки v063

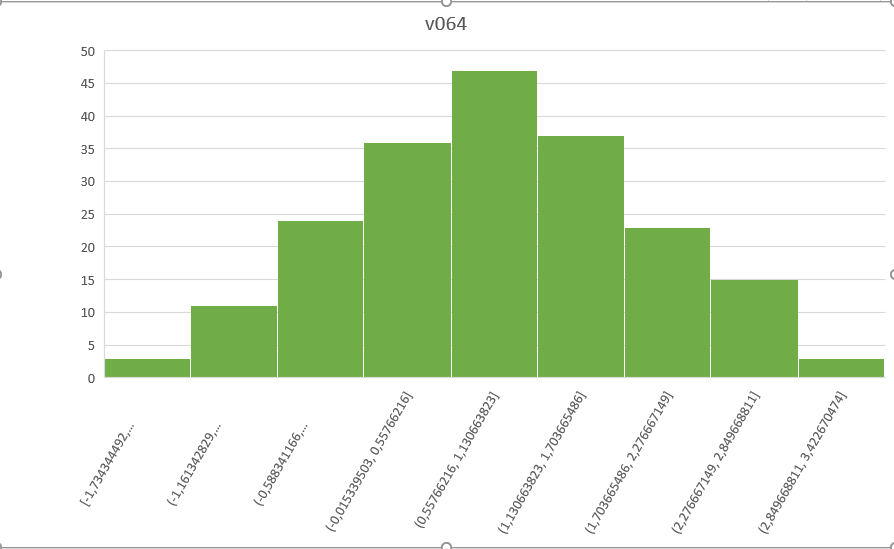
Рисунок 4 – Гистограмма выборки v064

Наибольшая асимметрия и разброс наблюдаются в выборке v062. Выбросы присутствуют в выборках v061 и v064, что видно по их гистограммам частот, где есть столбцы с высотой, близкой к нулю.

Анализ гистограммы выборки v063 позволяет предположить, что она распределена по равномерному закону и соответствует случайной величине Z, так как столбцы на гистограмме примерно одинаковы по высоте.

Выборки v061 и v064 относятся к случайным величинам X и Y, распределенным по нормальному закону. Это видно из их гистограмм частот, где наибольшие значения частоты находятся в центральных интервалах. График частот плавно возрастает от нуля, достигает максимума, затем плавно убывает.

Предполагается, что выборка v062 соответствует распределению Пуассона случайной величины D, так как ее гистограмма частот наиболее асимметрична.

3. Вычисление основных выборочных характеристик

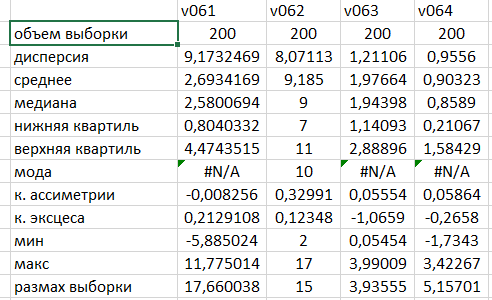
4. По результатам пп. 1-2 определить, какие массивы соответствуют величинам с нормальным, равномерным и Пуассоновским распределением.

Выборка v063 соответствует равномерному распределению, так как ее значение коэффициента асимметрии = 0,05554 и близко к 0, что характерно нормальному распределению, и коэффициент эксцесса = -1.0659, что приблизительно равно каноническому значению -1.2. Столбцы гистограммы частот приблизительно равны по высоте.

Выборки v061 и v064 распределены по нормальному закону так как их коэффициенты асимметрии и эксцесса близки к 0, что соответствует нормальному закону распределения и гистограммы частот данных выборок имеют формы пиковую. Чем ближе значение элемента выборки к среднему, тем чаще он в ней встречается.

Выборка v062 соответствует распределению Пуассона, так как она имеет наибольший коэффициент асимметрии, гистограмма асимметрична

2. Оценивание параметров.

1. Несмещенные точечные оценки

Выборка v063 соответствует случайной величине Z, имеющей равномерное распределение 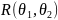. Точечные оценки:

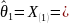0,054543

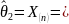3,99009

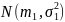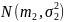Согласно предположению, выборки v061 и v064 соответствуют случайным величинам X и Y, которые распределены по нормальному закону и соответственно. Получим их точечные оценки:

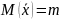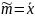Известно, что , следовательно является несмещенной оценкой.

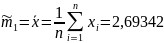
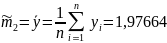
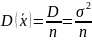. Возьмем в качестве точечной оценки D = D(X) выборочную дисперсию D_в. Так как ,

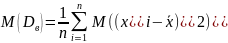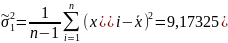
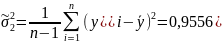
Выборка v062 соответствует случайной величине D, имеющей распределение Пуассона .

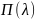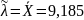
2. Найти доверительные оценки параметров нормальных распределений и распределения Пуассона.

Найдем доверительные оценки параметров нормальных распределений и . Как было предположено ранее данным распределениям соответствуют выборки v061 и v064.

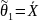
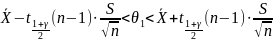
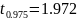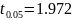Выберем доверительный коэффициент на уровне γ=0.95. По таблице Стьюдента . По таблице Стьюдента . . По таблице распределения хи-квадрат 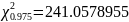и .

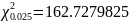Тогда получим для выборки v061:

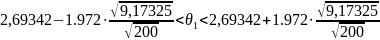
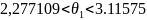
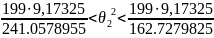
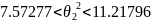
Тогда получим для выборки v064:

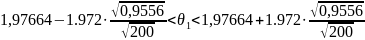
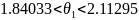
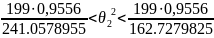
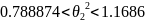
Найдем доверительную оценку параметра 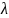случайной величины D, распределённой по закону Пуассона (выборка v062).

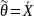
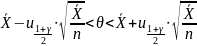
Согласно таблице квантилей нормального распределения, получим

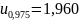
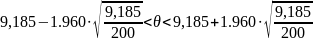
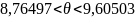
3. Проверка статистических гипотез.

Используя критерий согласия χ², проверим выдвинутые ранее предположения о виде распределения каждой выборки.

Для выборки v063 гипотеза H₀ – распределена по равномерному закону. H₁ – не распределена по равномерному закону.

,

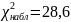
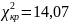
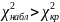следовательно на уровне значимости 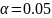гипотеза, что выборка v063 распределена по равномерному закону опровергается.

Для выборки v061 гипотеза H₀ – распределена по нормальному закону. H₁ – не распределена по нормальному закону.

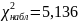
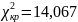
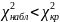, следовательно на уровне значимости гипотеза, что выборка v061 распределена по нормальному закону подтверждается.

Для выборки v064 пусть гипотеза H0 – распределена по нормальному закону. H₁ – не распределена по нормальному закону.

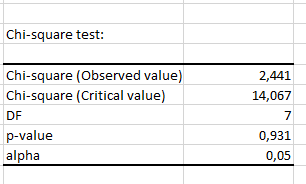
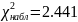
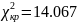
, следовательно на уровне значимости гипотеза, что выборка v064 распределена по нормальному закону, подтверждается.

Для выборки v062 пусть гипотеза H₀ – распределена по закону распределения Пуассона. H₁ – не распределена по закону распределения Пуассона.

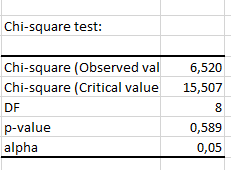
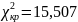
, следовательно на уровне значимости гипотеза, что выборка v062 распределена по закону распределения Пуассона подтверждается.

4. Вывод

На основании проведенного анализа были выдвинуты гипотезы, что выборки v061 и v064 соответствуют случайным величинам X и Y, распределённым по нормальному закону, выборка v062 соответствует распределению Пуассона для дискретной случайной величины D, а выборка v063 — равномерному распределению случайной величины Z. Проверка этих гипотез с помощью критерия согласия 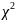подтвердила данные предположения