№94
Воронка
имеет форму конуса радиуса
см
и высоты
см,
обращенного вершиной вниз. За какое
время вытечет вся вода из воронки через
круглое отверстие диаметра
см,
сделанное в вершине конуса.
Решение.
Рассмотрим поперечное сечение конуса:
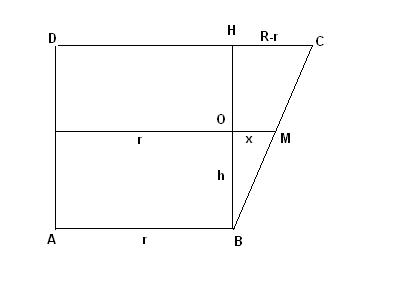
На рисунке
DA - высота конуса (показана только
половина сечения), DC - верхнее основание
конуса, АВ - нижнее основение конуса.
Пусть в некоторый момент времени t высота
уровня воды была
(отрезок
ОВ на рисунке). Найдем зависимость
радиуса верхней отметки R(t) уровня воды
от высоты уровня. Проведем в трапеции
ABCD
высоту
ВН. Из подобия треугольников BOM
и
ВНС
Откуда
Поскольку
будем
считать, что
Введем
обозначения радиусов момент времени
и
:
Приращение
объема воды за время
равно очевидно объему усеченного конуса
с радиусами оснований
и
и
высотой
,
взятого с противоположным знаком
(поскольку количество воды уменьшилось
за время
,
приращение отрицательное):
С другой стороны, приращение объема
Приравняв полученные разным способом приращения, получим уравнение:
При
Неизвестную
константу С найдем воспользовавшись
тем, что в начальный момент времени бак
был заполнен до верху:
Заменим
радиус нижнего отверстия на половину
диаметра:
Для нахождения времени подставляем h=0:
Откуда
