
4 лаба
.docxМинистерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ» (ТУСУР)
Кафедра комплексной информационной безопасности электронно-вычислительных систем (КИБЭВС)
Моделирование СМО с повторными заявками
Отчет по лабораторной работе №4
по дисциплине «Моделирование автоматизированных информационных систем»
Вариант №4
Студент гр.:
_______
__.__.2024
Руководитель
преподаватель каф. КИБЭВС
_______ Е.А. Прозорова
__.__.2024
Томск 2024
Введение
Цель работы – Исследовать систему массового обслуживания (СМО) М/М/1/0 (система Эрланга) с повторными (в т.ч. «настойчивыми») заявками: построить имитационную модель системы и получить значения параметров ее функционирования. Изучить способы получения усредненных значений параметров системы в ходе имитационного моделирования. Проверить основные теоретические формулы.
2 ХОД РАБОТЫ
Была собрана модель, соответствующая системе массового обслуживания (СМО) М/М/1/0 с настойчивыми заявками (рисунок 2.1).

Рисунок 2.1 – Модель в программе
Была установлена длительность одного запуска (репликации) Trep и число запусков – Nrep в соответствии с вариантом 4: Количество повторений эксперимента с моделью равно 4, а длительность одного запуска (репликации) равно 100 часов (рисунок 2.2).

Рисунок 2.2 – Параметры репликации
Для блока Create в соответствии с вариантом было задано время между поступлениями заявок и время поступления первой заявки как экспоненциально распределенную случайную величину со средним значением равным MTBA (рисунок 2.3).
В блоке Process был создан ресурс, для которого время обслуживания заявки будет представлять собой экспоненциально распределенную случайную величину со средним значением MST≈5/9*MTBA (рисунок 2.4).

Рисунок 2.3 – Блок Create

Рисунок 2.4 – Блок Process
Для заявок, получивших отказ в обслуживании, был задан атрибут, содержащий время до следующей попытки обращения к серверу. Время до следующей попытки (Mean Retry Time) распределено экспоненциально со средним значением MRT=MTBA+MST (рисунок 2.5).

Рисунок 2.5 – Блок Assign Attribute
Зафиксировав значения MST и MRT, проведем моделирование работы СМО, изменяя значение MTBA в пределах 0.8-1.2 от заданного по варианту. По завершению моделирования сведем в таблицу 2.1 следующие показатели:
среднее число заявок на орбите;
среднее время пребывания на орбите:
долю заявок, занявших сервер с первой попытки;
загрузку сервера;
среднее количество попыток обращения к серверу.
Таблица 2.1 – Моделирование с измененным MTBA
Nrep=4, Trep=100 |
MTBA, сек |
|
|
w |
wтеор |
Pw=0, % |
Pw=0, теор. % |
|
Nretry |
MST=35.5 MRT=99.5 |
51.2 |
1.5722 |
1.5564 |
0.02215 |
0.021 |
1.0049 |
1 |
0.68509 |
2 |
57.6 |
0.97524 |
0.971222 |
0.01556 |
0.015 |
1.0057 |
1 |
0.61022 |
6 |
|
64 |
0.66644 |
0.65 |
0.01585 |
0.016 |
0.99383 |
1 |
0.54128 |
0 |
|
70.4 |
0.51482 |
0.5 |
0.01004 |
0.01 |
0.99380 |
1 |
0.49697 |
1 |
|
76.8 |
0.76442 |
0.75634 |
0.00795 |
0.00786 |
1.0233 |
1.03 |
0.44654 |
1 |
Далее построим графики зависимости указанных величин от интенсивности поступления заявок (рисунки 2.6 – 2.10).

Рисунок 2.6 – Зависимость среднего числа заявок на орбите от интенсивности поступления заявок

Рисунок 2.7 – Зависимость среднего времени пребывания на орбите от интенсивности поступления заявок

Рисунок 2.8 – Зависимость доли заявок, занявших сервер с первой попытки от интенсивности поступления заявок
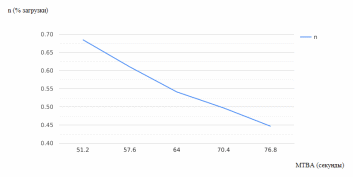
Рисунок 2.9 – Зависимость загрузки сервера от интенсивности поступления заявок

Рисунок 2.10 – Зависимость среднего количества попыток обращения к серверу от интенсивности поступления заявок
Затем были построены гистограммы числа попыток обращения к серверу для двух различных значений варьируемой величины MTBA равной 64 и 128 при двукратной длине репликации равной 200: (рисунки 2.11 – 2.12).

Рисунок 2.11 – Первая попытка

Рисунок 2.12 – Вторая попытка
Далее было произведено моделирование с зафиксированными значениями MTBA и MRT и изменяющимся значением MST, полученные значения были занесен в таблицу 2.2 и на их основе построены графики зависимостей от интенсивности обслуживания (рисунки 2.13 – 2.17).
Таблица 2.2 – Моделирование с измененным MST
Nrep=4, Trep=100 |
MST, сек |
|
|
w |
wтеор |
Pw=0, % |
Pw=0, теор. % |
|
Nretry |
MTBA=64 MRT=99.5 |
28.4 |
0.31999 |
0.31 |
0.00570 |
0.005 |
0.97235 |
0.97 |
0.43896 |
0 |
31.95 |
0.46772 |
0.45 |
0.00834 |
0.008 |
1.0088 |
1 |
0.48283 |
0 |
|
35.5 |
0.66644 |
0.65 |
0.01192 |
0.011 |
0.99383 |
1 |
0.54128 |
0 |
|
39.05 |
0.84755 |
0.8256578 |
0.01516 |
1.015 |
0.98146 |
0.98 |
0.60232 |
1 |
|
42.6 |
1.2846 |
1.27 |
0.02291 |
0.022 |
0.97881 |
0.97 |
0.65733 |
0 |

Рисунок 2.13 – Зависимость среднего числа заявок на орбите от интенсивности поступления заявок

Рисунок 2.14 – Зависимость среднего времени пребывания на орбите от интенсивности поступления заявок

Рисунок 2.15 – Зависимость доли заявок, занявших сервер с первой попытки от интенсивности поступления заявок

Рисунок 2.16 – Зависимость загрузки сервера от интенсивности поступления заявок

Рисунок 2.17 – Зависимость среднего количества попыток обращения к серверу от интенсивности поступления заявок
Далее было произведено моделирование с зафиксированными значениями MTBA и MST и изменяющимся значением MRT, полученные значения были занесен в таблицу 2.3 и на их основе построены графики зависимостей от интенсивности обслуживания (рисунки 2.18 – 2.22).
Таблица 2.3 – Моделирование с измененным MRT
Nrep=4, Trep=100 |
MRT, сек |
|
|
w |
wтеор |
Pw=0, % |
Pw=0, теор. % |
|
Nretry |
MTBA=64 MST=35.5 |
59.7 |
0.62392 |
0.61 |
0.01114 |
0.01 |
0.98715 |
0.98 |
0.54398 |
0 |
79.6 |
0.72442 |
0.716945 |
0.01266 |
0.01255 |
0.98562 |
0.99 |
0.55787 |
0 |
|
89.55 |
0.61178 |
0.6114 |
0.01094 |
0.01 |
0.99600 |
1 |
0.54318 |
1 |
|
99.5 |
0.63147 |
0.62 |
0.01125 |
0.011 |
0.96095 |
0.96 |
0.54359 |
1 |
|
109.45 |
0.64788 |
0.64555 |
0.01169 |
0.012 |
1.0030 |
1 |
0.53895 |
0 |
|
119.4 |
0.66609 |
0.65 |
0.01196 |
0.01053 |
1.0242 |
1 |
0.54113 |
0 |
|
139.3 |
0.64069 |
0.64 |
0.01149 |
0.011 |
1.0155 |
1 |
0.54220 |
2 |

Рисунок 2.18 – Зависимость среднего числа заявок на орбите от параметра MRT

Рисунок 2.19 – Зависимость среднего времени пребывания на орбите от параметра MRT

Рисунок 2.20 – Зависимость доли заявок, занявших сервер с первой попытки от параметра MRT

Рисунок 2.21 – Зависимость загрузки сервера от параметра MRT

Рисунок 2.22 – Зависимость среднего количества попыток обращения к серверу от параметра MRT
Затем были сравнены способы сбора статистики в Arena - Time-persistent и Tally. Результаты сравнения были сведены в таблицу 2.4.
Таблица 2.4 – Результаты сравнения способов сбора статистики
MTBA=64, MST=35.5, MRT =99.5, Trep=100 |
||||
№ реп |
Источники данных (число заявок на орбите) |
|||
Теоретическое |
Базовый отчёт |
Tally |
Time-Persistent |
|
1 |
0.99 |
0.99383 |
0.93007 |
1 |
2 |
1 |
0.99840 |
0.91072 |
1 |
3 |
1 |
1.0038 |
0.93982 |
1 |
4 |
1 |
1.0084 |
0.96235 |
1 |
На основании проделанных моделирований и полученных данных, можно сделать выводы:
Среднее время между поступлениями заявок (MTBA) напрямую влияет на интенсивность потока заявок в систему. Увеличение MTBA приводит к снижению нагрузки на систему, что, в свою очередь, может уменьшить среднее время ожидания и размер очереди. Среднее количество заявок в системе: уменьшается с увеличением MTBA. Среднее время ожидания: также уменьшается, что указывает на более эффективное обслуживание;
Среднее время обслуживания (MST) является критическим параметром, определяющим скорость обработки заявок. Увеличение MST приводит к увеличению времени ожидания и размера очереди. Это связано с тем, что при более длительном обслуживании ресурсы системы становятся менее доступными для новых заявок;
Среднее время до повторного обращения (MRT) также существенно влияет на параметры функционирования СМО. Если MRT высоко, это может привести к увеличению общего числа попыток обращения к ресурсу, что негативно скажется на показателях системы. Число повторных попыток: увеличивается с ростом MRT, что может привести к большему количеству потерянных заявок. Вероятность отказа: увеличивается при высоком MRT, что указывает на низкую эффективность системы в условиях высокой загруженности.
Далее была собрана модель, соответствующую СМО М/М/1/0 с повторными заявками (рисунок 2.23).

Рисунок 2.23 – Собранная модель
Была установлена длительность одного запуска (репликации) Trep и число запусков – Nrep в соответствии с вариантом 4: Количество повторений эксперимента с моделью равно 4, а длительность одного запуска (репликации) равно 100 часов (рисунок 2.24).

Рисунок 2.24 – Параметры репликации
Для блока Create в соответствии с вариантом было задано время между поступлениями заявок и время поступления первой заявки как экспоненциально распределенную случайную величину со средним значением равным MTBA (рисунок 2.25).
В блоке Process был создан ресурс, для которого время обслуживания заявки будет представлять собой экспоненциально распределенную случайную величину со средним значением MST≈2/3*MTBA (рисунок 2.26).

Рисунок 2.25 – Блок Create

Рисунок 2.26 – Блок Process
Для заявок, получивших отказ в обслуживании, был задан атрибут, содержащий время до следующей попытки обращения к серверу. Время до следующей попытки (Mean Retry Time) распределено экспоненциально со средним значением MRT=MTBA+MST (рисунок 2.27).
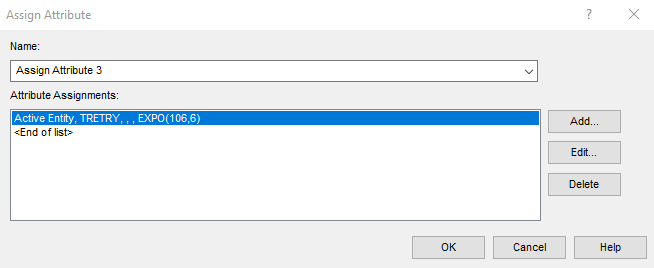
Рисунок 2.27 – Блок Assign Attribute
Затем была проведена серия экспериментов, по завершении которой полученные данные свели в таблицу 2.5.
Таблица 2.5 – Результаты новой серии экспериментов
Nrep=4, Trep=100 |
q |
|
|
|
|
|
|
Pw=0, % |
Pw=0, теор. % |
MTBA=64 MST=42,6 MRT=106,6 |
0.1 |
0.42370 |
0.42331 |
0.0858 |
0.085 |
0.47822 |
0.47 |
0.88420 |
0.88 |
0.3 |
0.50150 |
0.50131 |
0.2411 |
0.22 |
0.40494 |
0.40 |
0.74894 |
0.72484 |
|
0.5 |
0.18521 |
0.18531 |
0.3426 |
0.334 |
0.35685 |
0.355 |
0.66239 |
0.65 |
|
0.7 |
0.15125 |
0.1532 |
0.4165 |
0.4 |
0.31422 |
0.3113 |
0.58353 |
0.57683 |
|
0.9 |
0.11503 |
0.11 |
0.4775 |
0.46749 |
0.28381 |
0.28222 |
0.51941 |
0.5 |
Затем были построены графики зависимостей указанных величин от параметра q (рисунки 2.28 – 2.31).

Рисунок 2.28 – Зависимость среднего числа заявок на орбите от параметра q

Рисунок 2.29 – Зависимость загрузки сервера от параметра q

Рисунок 2.30 – Зависимость доли заявок, занявших сервер с первой попытки, от параметра q

Рисунок 2.31 – Зависимость общего процента не обслуженных (потерянных) заявок от параметра q
Далее в таблицу 2.7 были сведены следующие значения:
среднее количество попыток обращения повторных заявок к серверу (по обслуженным заявкам);
среднее количество попыток обращения повторных заявок к серверу (по потерянным заявкам);
среднее время пребывания заявки в системе (по обслуженным заявкам);
среднее время пребывания заявки в системе (по потерянным заявкам).
Затем в Arena были построены гистограммы (для обслуженных и для потерянных заявок) среднего числа попыток обращения к серверу для двух различных значений любой варьируемой величины (q или MRT соответственно) (рисунки 2.32 – 2.33). Использована одна репликация двукратной длины.

Рисунок 2.32 – Гистограмма среднего числа попыток обращения к серверу для величины q для обслуженных заявок

Рисунок 2.33 – Гистограмма среднего числа попыток обращения к серверу для величины q для потерянных заявок
Далее проведем моделирование работы СМО, зафиксировав значения MTBA и MST и приняв вероятность ухода из системы равной 0.33, изменяя значение MRT в пределах 0.5-1.5 от заданного по варианту.
Полученные значения занесем в таблицу 2.6, на их основе построим графики зависимости величин от вероятности q (рисунки 2.34 – 2.37).
Таблица 2.6 – Результаты новой серии экспериментов
Nrep=4, Trep=100 |
MRT, сек |
|
|
, % |
% |
|
|
Pw=0, % |
Pw=0, теор. % |
MTBA=64 MST=42,6 q=0.33 |
59.7 |
0.26107 |
0.26 |
0.2569 |
0.25678 |
0.40285 |
0.4 |
0.74551 |
0.7432 |
79.6 |
0.28622 |
0.27490 |
0.2534 |
0.25363 |
0.40262 |
0.4 |
0.72894 |
0.7232 |
|
89.55 |
0.27150 |
0.2632 |
0.2524 |
0.2528 |
0.40572 |
0.4 |
0.75332 |
0.7532 |
|
99.5 |
0.29345 |
0.29 |
0.2486 |
0.2489 |
0.40477 |
0.4 |
0.75265 |
0.7532 |
|
109.45 |
0.29759 |
0.3 |
0.2611 |
0.2611 |
0.40812 |
0.41 |
0.74071 |
0.7432 |






 ,
%
,
% %
%

