Закон Архимеда.
Силы гидростатического давления действующие на боковые грани, действующие грани равны по назначению и противоположны по направлению поэтому они уравновешены. Сила гидростатического давления действующая на основание призмы не одинаковы. На верхнее основание действует, которая направлена вниз, а на нижнее вверх.
Сила
Архимеда( сила выталкивания)
На любой глубине сила выталкивания одинакова.
Закон Архимеда (формулировка)
На погруженное в жидкость тело действует равнодействующая сила гидростатического давления ( Архимедова сила) направленная вверх и равная весу жидкости, объем который равен объему погруженной части тела.
Основы гидродинамики
Виды движения жидкости: установившееся, неустановившееся ,равномерно и неравномерное, напорное и безнапорное, плавноизменяющееся движение жидкости.
Неустановившимся (нестационарным) называется движение, когда скорость течения и давление зависят от координат точки и изменяются во времени:
,
.
Примерами неустановившегося движения жидкости могут служить, например: истечение жидкости через отверстие из резервуара, если уровень в нём меняется; истечение жидкости из аккумулятора при изменении давления газа в нём; течение жидкости в трубопроводе с включённым в гидросистему поршневым насосом.
Установившимся (стационарным) называется движение жидкости, при котором скорость и давление являются функциями только координат и не зависят от времени.
,
.
Установившееся движение может быть равномерным и неравномерным.
При равномерном движении скорость и давление в соответствующих точках сечения по длине остаются постоянными, т.е. поле скоростей остаётся неизменным вдоль потока.
При неравномерном движении скорость, давление и плотность могут изменяться с изменением координат движущейся частицы жидкости.
Исследование установившихся течений значительно проще, чем неустановившихся.
Безнапорное движение происходит в открытых системах и осуществляется за счёт сил тяжести. Например, движение воды в реках, каналах, трубах при неполном их заполнении.
Напорное движение происходит в закрытых системах (трубопроводах), когда поток со всех сторон окружён твёрдыми стенками и движение осуществляется за счёт разности давлений по длине потока. Например, движение жидкости в трубопроводе от насоса.
Плавноизменяющееся движение
П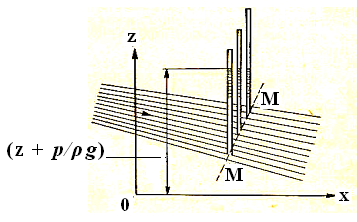
лавноизменяющимся называется
такое движение жидкости, при котором
кривизна струек и угол расхождения
между ними весьма малы.Рис.23
С
достаточной точностью для практики
можно считать, что при плавноизменяющемся
движении для всех точек данного живого
сечения, например сечения М-М (рис.
23), давление изменяется по гидростатическому
закону 
, a
удельная потенциальная энергия
одинакова, т. е.
Траектория, линия тока, элементарная струйка. Свойства элементарной струйки.
Линией тока называется линия, в каждой точке которой вектор скорости в данный момент времени направлен по касательной. Это понятие является центральным в методе Эйлера.
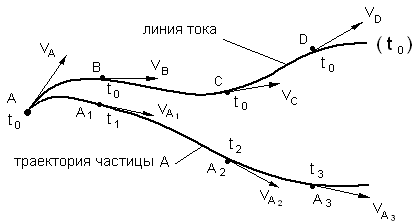
Рис. 3.3. Линия тока и траектория частицы жидкости
Траекторией называется
путь, который описывает точка при своём
движении. При
установившемся движении линия
тока и траектория частицы совпадают.
В общем случае неустановившегося
движения в следующий момент времени 
через
ту же точку А может проходить уже другая
линия тока.
Вектор
скорости 
с
компонентами
касателен
к линии тока, т.е. совпадает по направлению
с элементами линии тока
,
имеющего проекции
на
оси координат. Воспользуемся известным
условием параллельности двух векторов
– их проекции на оси координат должны
быть пропорциональны друг другу
.
Полученное условие является уравнением линии тока в дифференциальной форме.
В частном случае при установившемся движении каждая линия тока сохраняет своё положение в пространстве и одновременно становится линией, по которой перемещаются частицы, т.е. совпадает с траекторией.
Э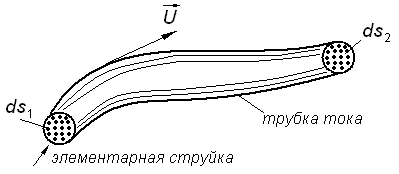
лементарной
струйкой называется
совокупность линий тока, проходящих
через все точки бесконечно малой
площадки 
(рис.3.4).
При установившемся движении элементарная струйка сохраняет с течением времени постоянными свою форму, размеры и положение в пространстве, что является следствием аналогичного свойства составляющих её линий тока.
При стремлении поперечных размеров струйки к нулю она в пределе стягивается в линию тока.
Боковая поверхность элементарной струйки называется трубкой тока (рис.3.4). Трубка тока, таким образом, является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток.
В случае установившегося движения элементарная струйка обладает следующими тремя свойствами:
1) Форма элементарной струйки не меняется во времени, т.к. при установившемся движении не меняется форма линий тока;
2) Поверхность элементарной струйки (трубки тока) непроницаема, т.е. перетекание через боковые стенки отсутствует. Частицы жидкости, движущиеся в одной линии тока, не могут принадлежать другим;
3) Скорость и давление для всех точек данного поперечного сечения струйки постоянны, однако вдоль струйки эти величины могут меняться.