Центр давления

Точка приложения результирующей силы давления жидкости на любую поверхность называется центром давления.

Применительно к рис. 2.12 центром давления является т. D. Определим координаты центра давления (x_D; z_D) для любой плоской поверхности.

Из теоретической механики известно, что момент равнодействующей силы относительно произвольной оси равен сумме моментов составляющих сил относительно той же оси. За ось в нашем случае примем ось Ох (см. рис. 2.12), тогда

Известно также, что   является моментом инерции площади   относительно оси Ox 

В результате получаем

откуда

Подставим в это выражение формулу (2.9) для F и геометрическое соотношение  :

Перенесем ось момента инерции в центр тяжести площадки  . Обозначим момент инерции относительно оси, параллельной оси Ох и проходящей через т.С, через  . Моменты инерции относительно параллельных осей связаны соотношением

;

тогда   и окончательно получим

 (2.11)

Формула показывает, что центр давления расположен всегда ниже центра тяжести площадки, за исключением случая, если площадка горизонтальна и центр давления совпадает с центром тяжести. Для простых геометрических фигур моменты инерции относительно оси, проходящей через центр тяжести и параллельной оси Ох (рис. 2.12), определяются по следующим формулам:

для прямоугольника

 (2.12)

где сторона основания параллельна Ох;

для равнобедренного треугольника

 (2.13)

где сторона основания параллельна Ох;

для круга

 (2.14)

10. Сила давления жидкости на криволинейные стенки.

Рассмотрим действие жидкости на цилиндрические или сферические поверхности, имеющие вертикальную плоскость симметрии. Сила давления жидкости в этом случае сводится к равнодействующей силе, лежащей в плоскости симметрии.

В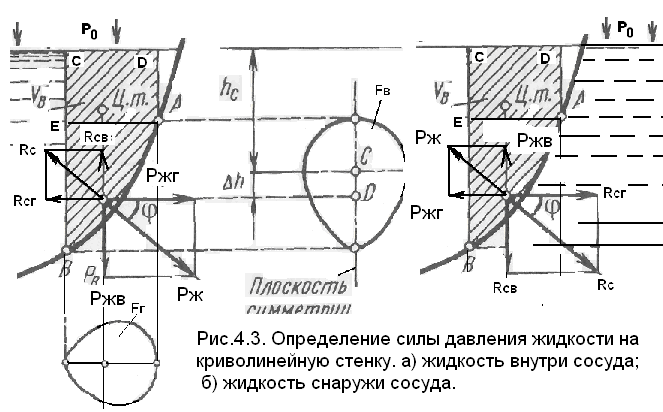 озьмем криволинейную поверхность АВ, образующая которой перпендикулярна к плоскости чертежа (рис.4.3а), определим силу давления жидкости на эту поверхность. 

Выделим объем жидкости, ограниченный поверхностью АВ, вертикальными плоскостями, проведенными через границы этого участка ВС и AD, свободной поверхностью жидкости. Рассмотрим условия равновесия объема АВСD в вертикальном и горизонтальном направлениях.

Сила давления жидкости P действует на стенку АВ, стенка АВ удерживает действие жидкости силой реакции стенки Rс =P, направленной в противоположную сторону. На рис. 4.3 сила реакции стенки и сила давления жидкости разложены на горизонтальные и вертикальные составляющие.

Условие равновесия объема АВСD в вертикальном направлении имеет вид

Rс_в =Pжв= Р₀F_г + G= Р₀F_г + ρgV₀, (4.8)

где Р₀- давление на свободной поверхности жидкости; F_г - площадь горизонтальной проекции поверхности АВ;G- вес выделенного объема жидкостиV_0.ОбъемV₀ называют – объем тела давления..

Условие равновесия того же объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности ЕС и АDвзаимно уравновешиваются и остается лишь сила давления на площадь ВЕ т. е. на вертикальную проекцию поверхности S_в=L_EB*B. Тогда

Rсг=Pжг= F_вρgh_c+ F_в Р₀ = F_в(ρgh_c+ Р₀).(4.9)

Определив по формулам (4.8) и (4.9) вертикальную и горизонтальную составляющие полной силы Рж, найдем , (4.10).

Сила давления жидкости на криволинейную стенку будет равна сила реакции стенки Rж =Pи направлена в противоположную сторону.

Когда жидкость расположена снаружи (рис.4.3б), сила гидростатического давления на криволинейную поверхность АВ определяется также, но направление ее будет противоположным.

При этом под величиной G следует понимать так же, как и в первом случае вес жидкости в объеме АВСD, хотя этот объем и не заполнен жидкостью.

Положение центра давления на цилиндрической стенке можно найти, если известны силы Fв и Fги определены центр давления на вертикальной проекции h_D стенки и центр тяжести выделенного объема АВСD.