18.1. Истечение жидкости через внешние цилиндрические насадки

При входе в насадку происходит сжатие струи внутри насадка, так же как и при истечении из малого отверстия. За сжатым сечением площадью ω_с следует расширение струи до поперечного сечения самой насадки. Непосредственно в зоне сжатого сечения возникает вихреобразование в виде кольцевой водоворотной области. Скорость струи в сжатом сечении существенно больше скорости на входе в насадку, в результате этого в этой области давление становится меньше атмосферного, т. е. создается вакуумметрическое давление.

Максимальное вакуумметрическое давление p_вак будет иметь место непосредственно в сжатом сечении. На границе водоворотной области ближе к выходу из насадки p_вак = 0. Все выше изложенное можно доказать, используя уравнение Бернулли. Для получения формулы р асхода для цилиндрической насадки рассмотрим схему, представленную на рис. 18.1.1.

Рис. 18.1.1.

Запишем уравнение Бернулли относительно плоскости сравнения 0-0, проходящей по оси насадки. Сечение 1-1 принимаем по свободной поверхности жидкости в резервуаре, а сечение 3-3 на выходе из насадки. Давление на поверхности жидкости в резервуаре p_а, а истечение жидкости осуществляется в атмосферу

z₁ +   +  = z₃ +   +   + h_w.

Скоростью υ₁ в резервуаре пренебрегаем. Принимаем α₃  1; z₁ = H; p₁ = p_а; p₃ = p_а; z₃ = 0; υ₃ = υ.

Гидравлические потери на участке от 1-1 до 3-3 с учетом потерь по длине

h_w =  .

В результате, после соответствующих подстановок, получим

H =   +   = (1+ )  ,

где   - суммарный коэффициент сопротивления на участке от 1-1 до 3-3.

Потери напора, возникающие при движении жидкости через насадки, можно разделить как

h_w = h_r1-2 + h_rвр +h_l,

где h_r1-2 – потери напора от свободной поверхности (сечение 1-1) до сжатого сечения с-с (сечение 2-2)

h_r1-2 = ζ_1-2  ,

h_rвр – потери напора между сечениями 2-2 (сжатое сечение) и полным живым сечением на выходе из насадки (сечение 3-3). Считаем их как потери напора при внезапном расширении

h_rвр = ζ_вр  .

Коэффициент местных сопротивлений при внезапном расширении

ζ_р =  ,

где ε – коэффициент сжатея, ε =  ; h_l – потери напора по длине насадки

h_l = ζ_дл  = λ    ,

 = ζ_1-2 + ζ_р + ζ_дл.

Тогда потери напора в насадке

h_w =  .

Скорость потока жидкости на выходе из насадки

υ =    .

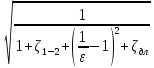
Обозначим коэффициент скорости насадки

φ_н =  .

Формула скорости истечения из насадки окончательно представляется в известном ранее виде

υ = φ_н  .

Расход жидкости, проходящий через насадку

Q = ω υ = φ_нω .

Так как насадка не имеет сжатия на выходе из него, то ε = 1, и для цилиндрической насадки коэффициент расхода насадки μ_н равен коэффициенту скорости

μ_н = εφ_н = φ_н.

в результате проведения опытов установлено, что при длине насадки l = (2 4)d можно не учитывать сопротивление по длине насадки, ζ_дл = 0.

При достаточно больших значениях числа Re сумма коэффициентов ζ_1-2 (коэффициент на сужение потока) и ζ_вр (расширение потока) в среднем, как показали численные подсчеты, равна

ζ_сум = ζ_1-2 + ζ_вр  0,50.

В результате скорость на выходе

υ =    .

Для цилиндрической насадки коэффициент скорости

φ_н =   =  0,82.

В случае, когда длина насадка l  4d, следует учитывать потери напора по длине

 = ζ_с + ζ_дл = 0,50 + λ .

Коэффициент скорости

φ_н =   =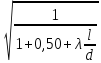 

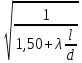
Так как φ_н = μ_н, то коэффициент расхода при l  4d

μ_н =  .

В результате увеличения скорости υ_с в сжатом сечении возрастает вакуумметрическое давление. При значительной разности атмосферного давления и вакуумметрического давления воздух может поступать в насадки через выходное сечение. В результате поток будет полностью отрываться от стенок насадки и будет происходить срыв вакуума. Насадка будет работать как при истечении из отверстия. Расход, проходящий через насадку, уменьшится и будет соответствовать расходу как из отверстия в тонкой стенке.

Найдем величину вакуумметрического давления, имеющего место в сжатом сечении. Напишем уравнение Бернулли для сечений 2-2 (сжатое сечение с-с) и 3-3 на выходе из насадки. Плоскость сравнения проведем по оси насадки.

z₂ +   +  = z₃ +   +  +h_w,

z₂ = z₃ = 0; p₂ –абсолютное давление, p₂ = p_2аб; p₃ = p_а.

Пpинимаем α₁ = α₃  1; υ₂ = υ_с; υ₃ = υ.

h_w – гидравлические потери на участке от сечения 2-2 до 3-3.

Потери напора по длине принимаем h_l = 0.

Потери напора h_w приближенно определяем как потери напора на внезапном расширении, h_w = h_wвр.

После подстановки получим

+  =   +  + ζ_вр  .

Вакуумметрический напор

 =   -  .

Тогда

=   - (1 + ζ_р) 

Коэффициент внезапного расширения

ζ_р =  .

Согласно уравнению неразрывности выразим скорость в сжатом сечении через υ

υ_с ω_с = υ ω = ε ω,

тогда

υ_с = υ   = υ  ,

где ε – коэффициент сжатия.

В результате вакуумметрический напор будет равен

 = .

Выражение, стоящее перед скоростным напором   преобразуем

=   – 1 -   +   – 1= 2 .

И тогда

 = 2 .

Выразим скорость υ через напор H

υ = φ_н  .

Заменим

= φ²H .

Как уже отмечалось ранее, для внешней цилиндрической насадки коэффициент скорости φ_н  0,82. Коэффициент сжатия струи в насадке принимаем ε   0,64. Согласно вышеизложенному определим вакуумметрический напор по последнему уравнению с учетом напора H

 = H_вак = 2 0,82² H 0, 76H.

Опытами установлено, что срыв вакуума происходит, когда максимальный вакуумметрический напор     8 м и начинается подсасывание воздуха через выходное отверстие насадки, а истечение жидкости осуществляется аналогично отверстию в тонкой стенке.

Предельное значение напора H, при котором истечение из насадки при l  (3 4) d без срыва вакуума, будет составлять

H_пр =  =    10,5м.

Таким образом, истечение струи из внешней цилиндрической насадки полным сечением будет происходить при H_вак 8м и предельным напором H_пр  10,5м при длине насадка l   (3 d/