35. Основные типы задач по расчету трубопроводов. Методика применения уравнения Бернулли для расчета трубопровода.

При расчете трубопроводов возможны 3 типа задач.

Первый тип задач: определение потребного напора H_потр для обеспечения заданного потребного расхода Q жидкости через трубопровода заданных размеров.

Исходные данные: расход Q ; давление p₂; плотность ρ и кинематическая вязкость v жидкости ; длина l и диаметр d трубопровода, качество поверхности трубы (относительная шероховатости Δ / d ).

Решение :

1. По исходному расходу Q и диаметру d находят скорость течения υ = 4Q/πd²

2. По υ, d и v находят Re = υd/ v и определяют режим течения,

3. Оценивают местные сопротивления и определяют коэффициенты 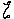  и потери напора h_м =  υ²/2g для ламинарного или турбулентного течения.

4. По числу Re и заданный шероховатости опр. коэффициенты Дарси λ_т.

5. По графикам или таблицам определяют сопротивление трубопровода К или модуль расхода К’ и решают основное уравнение ( Н_потр = Н_cт+ КQ^m) (4.1)

по которому находят потребный напор Н_потр.

Второй тип задач: определение расхода Q жидкости при заданных напоре и параметрах трубопровода.

Исходные данные: располагаемый напор Н_расп; ρ и v жидкости l и d трубопровода; относительная шероховатость Δ /d

Решение:

1.Определяют режим движения жидкости, так как для ламинарного и турбулентного течений методы решения разные.

Режим течения опр. путем сравнения располагаемого напора Н_расп с критическим напором Н_кр , который находят по основному уравнению (4.1).

2. При ламинарном течении Q находят и формулы (4.1), подставляя вместо Н_потр. располагаемый напор Н_расп; :

Q=1/K (Н_расп - Н_ст) = 1/К Н_расп.

С учетом Q = (πgd⁴/ 128vl) Н_расп

При турбулентном течении задачу решают методом последовательных приближений. Берут уравнение (1), в котором два неизвестных – Q и K; задаются значением λ_т с учетом шероховатости (λ_т = 0, 015…0,04); по формуле

 а m = 2 (4.2)

находят К и решают формулу (4.1) относительно Q. По найденному Q находят Re, а по найденному Re определяют λ_т .

Подставляют найденное значение λ_т в уравнение (4.2) и в указанном выше порядке находят Q, затем Re, а по Re ― новое значение λ_т и т.д. Вычисления ведут до тех пор, пока разница между значениями расхода, полученными в данном и предыдущем вычислениях, не станет незначительной, т.е. пока не будет обеспечена приемлемая точность.

3. Найти расход можно и графическим способом. Для этого нуж­но построить кривую потребного напора Н_потр = f(Q) для различ­ных λ_т. Задаются значениями Q, для которых подсчитывают υ, Re, λ_т, Н_потр. Строят указанную кривую. Затем по ординате H_потр= Н_расп находят нужную точку на оси абсцисс, т. е. искомый расход Q.

Третий тип задач: определение диаметра трубопровода (графическим

способом) для данной жидкости по заданным расходу и располагаемому на­пору.

Исходные данные: расход Q, располагаемый напор Н_расп, ρ и ν жидкости, длина трубопровода ℓ, относительная шероховатость Δ/d.

Решение.

1. Определяют режим течения, сравнивая Н_распр с критическим напором Н_кр.

Для этого используют уравнение (4.1) с учетом

а m = 1, (4.3)

преобразуя его с целью исключения неизвестного d:

Н_потр = Н_ст +  = Н_ст +   (4.4)

Отсюда

Н_кр = Н_ст +  . (4.5)

2. Для ламинарного течения искомый диаметр находят из формулы (4.1) с

учетом формулы (4.3):

Подсчитав d, определяют ближайший больший стандартный диаметр и по уравнению (4.1) уточняют значение напора по заданному расходу Q.

При турбулентном течении задаются рядом стандартных значений d и по уравнению (4.1) с учетом (4.2) определяют Н_потр по заданному расходу Q. Получив ряд значений Н_потр, строят график Н_потр = f(d) и по заданной ординате Н_расп определяют d, выбирают ближайший больший стандартный диаметр, после чего уточняют Н_потр.

При параллельном соединении: Q₂ + Q₃ + Q₄ = Q;

трубопроводов h_тр2 = h_тр3 = h_тр4.

При последовательном соединении: h_тр2 + h_тр3 + h_тр4 = h;

Q₂ = Q₃ = Q₄