Уравнение Бернулли для потока вязкой жидкости. Коэффициент кинетической энергии.
Примеры применения уравнения Бернулли в технике (расход Вентури, скоростная трубка)
Уравнение Бернулли описывает закон сохранения энергии для идеальной несжимаемой жидкости и находит широкое применение в различных областях техники. Вот несколько примеров его применения:
1. Вентури-эффект:
- Вентури-каналы используются для измерения расхода жидкости или газа. Когда жидкость проходит через сужение (Вентури-трубку), её скорость увеличивается, а давление падает. Разница давления до и после сужения позволяет вычислить объемный расход жидкости, что используется в различных системах, таких как водоснабжение, системы орошения и в химической промышленности.
2. Скоростные трубки:
- Скоростные трубки (или трубки Пито) применяются для измерения скорости потока жидкости или газа. Они работают по принципу уравнения Бернулли: когда поток жидкости проходит через трубку, создается разница давления между входом и выходом, которая пропорциональна квадрату скорости потока. Это позволяет точно измерять скорость потока в таких областях, как авиация (для измерения скорости самолетов) и в системах вентиляции.
3. Аэродинамика:
- Уравнение Бернулли используется для анализа потоков воздуха вокруг крыльев самолетов. Оно помогает объяснить подъемную силу, которая возникает из-за разницы давлений над и под крылом, что критически важно для проектирования самолетов.
4. Гидравлические системы:
- В гидравлических системах уравнение Бернулли помогает анализировать потоки в трубопроводах, насосах и других устройствах. Это позволяет оптимизировать проектирование систем, минимизируя потери энергии и обеспечивая эффективное распределение жидкости.
5. Системы отопления и охлаждения:
- В системах HVAC (отопление, вентиляция и кондиционирование воздуха) уравнение Бернулли применяется для расчета потоков воздуха и жидкости, что помогает в проектировании эффективных систем распределения тепла и холода.
Эти примеры демонстрируют, как уравнение Бернулли является важным инструментом для инженеров и ученых в различных областях техники.
Гидравлические сопротивления
Общие сведения о потерях энергии( напора).
Потери удельной энергии (напора), или, как их часто называют, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней. Гидравлические потери приблизительно пропорциональны скорости течения жидкости во второй степени, поэтому в гидравлике принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах:
,
(10.10)
или в единицах давления
.
(110.11)
Такое
выражение удобно тем, что включает в
себя безразмерный коэффициент
пропорциональности 
,
называемый коэффициентом потерь, или
коэффициентом сопротивления, значение
которого для данного русла в первом
грубом приближении постоянно.
Коэффициент потерь , таким образом, есть отношение потерянного напора к скоростному напору.
Гидравлические потери обычно разделяют на местные потери и потери на трение по длине.
Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы и размера русла, вызывающими деформацию потока. При протекании жидкости через местные сопротивления изменяется ее скорость и обычно возникают крупные вихри. Последние образуются за местом отрыва потока от стенок и представляют собой области, в которых частицы жидкости движутся в основном по замкнутым кривым или близким к ним траекториям.
Р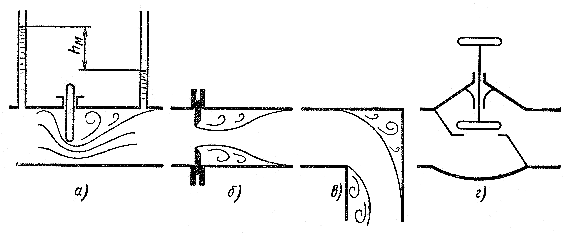
ис.
10.2.- Примеры местных сопротивлений(устройства).Там
же показаны отрывы потока и вихреобразования.
а - задвижка; б - диафрагма; в - колено; г - вентиль
Рис. 10.2. Схемы местных гидравлических сопротивлений
Местные потери напора определяются по формуле (10.10) следующим образом:
,(10.12)
или в единицах давления
.
(10.13)
Выражение
(10.12) часто называют формулой Вейсбаха.
В ней 
-
средняя по сечению скорость в трубе, в
которой установлено данное местное
сопротивление. Если же диаметр трубы
и, следовательно, скорость в ней
изменяются по длине, то за расчетную
скорость удобнее принимать большую из
скоростей, т.е. ту, которая соответствует
меньшему диаметру трубы.
Каждое местное сопротивление характеризуется своим значением коэффициента сопротивления , которое во многих случаях приближенно можно считать постоянным для данной формы местного сопротивления.
Потери
на трение по длине, - это потери энергии,
которые в чистом виде возникают в прямых
трубах постоянного сечения, т.е. при
равномерном течении, и возрастают
пропорционально длине трубы (рис. 10.3).
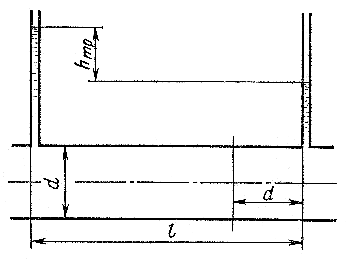
Рис. 10.3. Потери напора на трение по длине трубы
Потерю напора на трение можно выразить по общей формуле (10.10) для гидравлических потерь, т.е.
,
(10.14)
однако
удобнее коэффициент
связать
с относительной длиной трубы l/d.
Возьмем участок круглой трубы длиной,
равной ее диаметру, и обозначим его
коэффициент потерь, входящий в формулу
(10.14), через 
.
Тогда для всей трубы длиной l и
диаметром d коэффициент
потерь будет в l/d раз
больше:
.
(10.15)
В результате формула (10.14) примет вид:
,
(10.16)
или в единицах давления
.
(10.17)
Формулу (10.16) обычно называют формулой Дарси-Вейсбаха. Безразмерный коэффициент называют коэффициентом потерь на трение по длине, или коэффициентом Дарси.
Нетрудно выяснить физический смысл коэффициента , если рассмотреть условие равномерного движения в трубе цилиндрического объема длиной l и диаметром d(см. рис. 10.3), т.е. равенство нулю суммы сил, действующих на объем: сил давления и силы трения. Это равенство имеет вид
,
(10.18)
где 
-
напряжение трения на стенке трубы.
Если учесть формулу (10.17), то легко получить
,
(10.19)
т.е. коэффициент есть величина, пропорциональная отношению напряжения трения на стенке трубы к динамическому давлению, определенному по средней скорости.
Ввиду постоянства объемного расхода несжимаемой жидкости вдоль трубы постоянного сечения скорость и удельная кинетическая энергия также остаются постоянными, несмотря на наличие гидравлических сопротивлений и потерь напора.