
Двойные_Интегралы_v2
.3.pdf
Часть I
Двойные интегралы
Пусть имеется некоторая функция = ( , ), непрерывная в области
– замкнутая область на координатной плоскости x0y.
Пример (здесь по осям , отложена
: −10 ≤ ≤ 10, −10 ≤ ≤ 10, а по оси − (, ) = + 2 sin( )):
Двойной интеграл (, ) по области равен объему тела, заключенного между областью в 0 и множеством значений функции (, ) (см рис ниже)
Важнейшие свойства двойного интеграла:
1)(, ) = (, )
2)[ 1(, ) + 2(, )] = 1(, ) + + 2(, )
3)(, ) = 1 (, ) + +
2 (, ), где = 1 2, 1 ∩ 2 = 4) Если (, ) ≥ 0 в , то (, ) ≥ 0
Ниже без строгого обоснования будет приведен метод расстановки пределов в двойных интегралах.
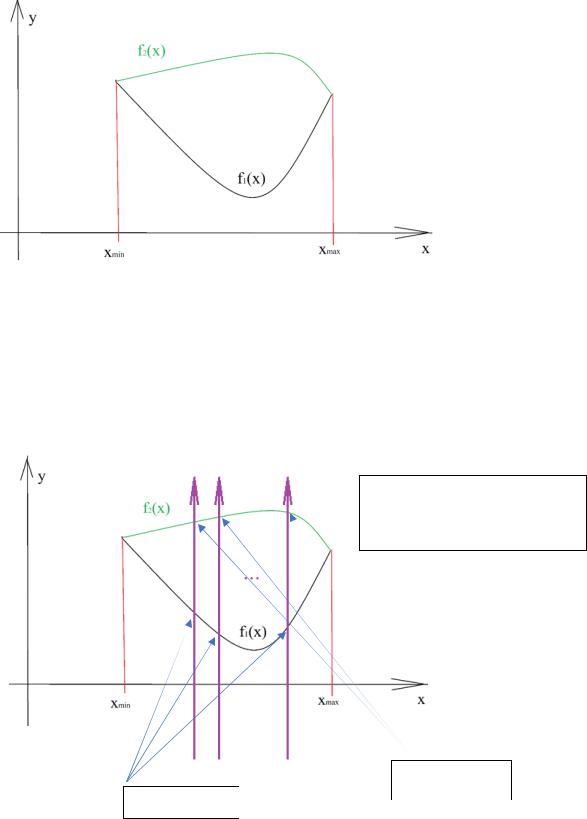
Пусть заданы область и функция ( , ). Изобразим на графике:
«Зажмем» область между двумя прямыми, параллельными оси 0 , пересекающими ось
абсцисс в точках и - максимальный и минимальный из области (см рис выше). Если любая прямая, параллельная 0 , пересекает область не более, чем в двух точках (крайний случай
пересечения в бесконечном количестве точек можно отбросить), то эта область называется правильной в направлении 0 .
Пусть область правильная в направлении 0 , а прямые, параллельные 0 и проходящие через( ; ), пересекают её в первый раз в точках 1( ) (точки "входа"), и второй раз в точках
2( ) (точки "выхода"):
Фиолетовые прямые пересекаютне более, чем в двух точках
входа и выхода
yвыхода = 2( )входа = 1( ) 

Тогда можно записать: |
|
|
|
|
|
|
||
|
|
≤ ≤ |
|
(область зажата между |
|
и |
) |
|
|
|
|
|
|
||||
{ 1( ) ≤ ≤ 2( ) (область сверху ограничена кривой 2, а снизу − кривой 1) |
||||||||
и перейти к повторному интегралу: |
|
|
|
|
||||
|
|
|
|
|
2( ) |
|
|
|
|
|
( , ) = ∫ |
∫ |
( , ) , (1) |
||||
|
|
1( ) |
|
|
Рассмотрим важные замечания: a) Запись
|
|
|
2( ) |
(, ) = ∫ |
∫ |
(, ) |
|
|
|
1( ) |
|
|
|
|
|
повторного интеграла – лишь упрощенная запись данного:
|
|
2( ) |
(, ) = ∫ |
(∫ (, )) |
|
|
|
1( ) |
|
|
|
Будьте внимательны: между и ∫ в выражении (1) не стоит знак умножения!1
b)В задачах, рассматриваемых в данном конспекте, двойной интеграл по области после вычисления дает число. Это значит, что внешний интеграл своими пределами всегда имеет числа, а переменная интегрирования внешнего интеграла всегда совпадает с переменной, от которой зависят функции, являющиеся пределами внутреннего интеграла:
Числа
Совпадают
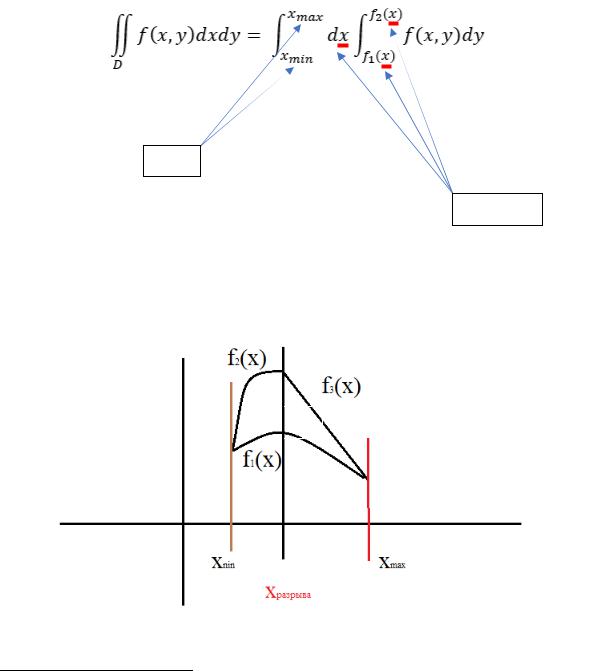
c)Если 2( ) или 1( ) непредставимы в виде одной функции, область надо разбивать на несколько частей и воспитывать их по отдельности:
1 
 2
2
1 Запись
|
( , ) = ∫ ∫ 2() |
( , ) = ∫ ∫ 2() |
( , ) будет серьёзной ошибкой |
||||
|
|
|
( ) |
|
|
( ) |
|
|
|
1 |
|
1 |
|
||
d)Аналогично правильности в направлении 0 можно ввести правильность в направлении 0 . Чтобы не загромождать конспект я опущу рассуждения (они полностью аналогичны приведенным выше), показав лишь результат:
|
|
( ) |
|
|
|
2 |
|
(, ) = ∫ |
∫ |
(, ), (2) |
|
|
|
( ) |
|
|
|
1 |
|
|
|
|
|
e)Обратите внимание: на иллюстрации к пункту (d) изображена область , являющаяся правильной в направлении 0, но не являющаяся правильной в направлении 0. Тем не менее, понятие правильности в определенном направлении не должно никого путать: от
одного случая к другому можно перейти простой заменой переменных = 1, = 1, после которой правильность в направлении 0 станет правильностью в направлении 01 и напротив: правильность в направлении 0 станет правильностью в направлении 01.
f)Совет: старайтесь избегать разбиения области на несколько других областей. Чаще всего можно либо сделать замену из пункта (е), либо (что в сущности то же самое) попробовать поменять направление.
g)Области, которые были «зажаты» между двумя иксами, будут сначала интегрироваться по ,
|
|
|
|
|
) . Можно |
||
затем по : ∫ |
|
(∫ 2 |
) , между игреками – напротив ∫ |
(∫ |
2 |
||
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
||
запоминать по более общему правилу (b).
h)Если область оказалась неправильной в некотором направлении, разбить ее на несколько правильных не получится! Верным действием в этом случае будет попытка интегрировать в другом направлении (сделать замену (е)) или поиск удачной замены переменных.
Поэтому перед тем, как расставлять пределы, бывает полезно проанализировать область на правильность в направлениях 0 и 0 , проверить необходимость разбиения области на подобласти.
Я предлагаю примерно такой алгоритм: проверяем правильность в обоих направлениях. Если в обоих правильная – выбираем то, при котором нужно будет разбить на наименьшее число подобластей. Если только одно из направлений правильное, расставляем пределы по нему.
Если оба неправильные – ищем замену переменных (в частности – пробуем полярную замену). В дальнейшем алгоритм будет усовершенствован и расписан чуть подробнее.
= , 0 ≤ ≤ 2
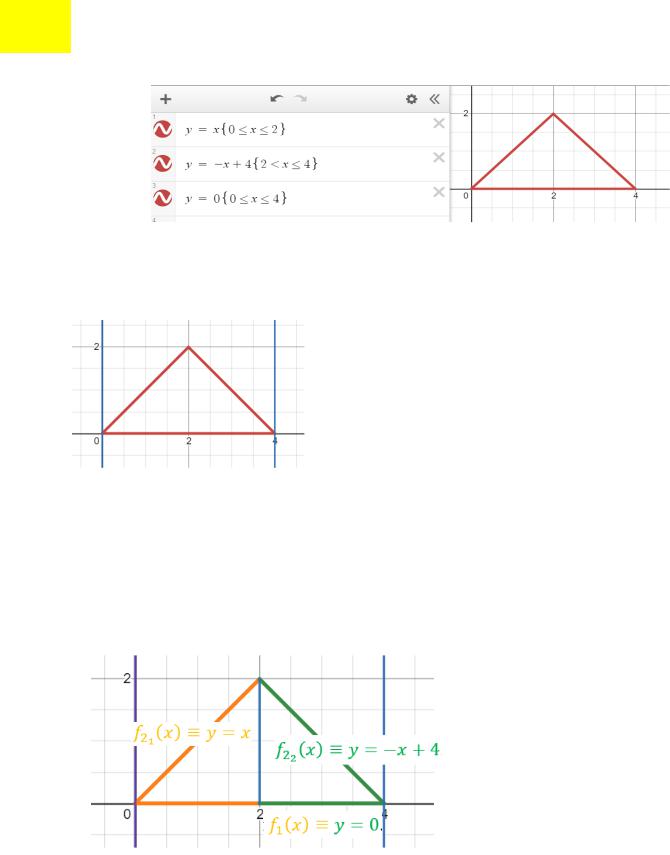
Пример 1: ( , ) = , : { = − + 4, 2 < ≤ 4, расставить пределы интегрирования и
= 0
вычислить интеграл двумя способами.
Для начала изобразим область:
I.Область правильная в обоих направлениях. Действительно: параллельные 0 или 0 прямые пересекают не более, чем в двух точках.
II.«Зажмем» область между прямыми = = 0 и = = 4:
III.Заметим, что нижний предел 1( ) ≡ = 0: проводим прямые из минус бесконечности, параллельные оси 0 , и определяем точки их пересечения с областью. Первое пересечение всегда в = 0, значит это и есть искомый нижний предел
IV. Верхний предел выразить одной функцией не удастся: при 0 ≤ ≤ 2 прямые, параллельные 0 , пересекут второй раз в точках, лежащих на прямой = , то есть верхним пределом на 0 ≤ ≤ 2 будет 21 ( ) ≡ = , а при 2 < ≤ 4 прямые, параллельные 0 , пересекут второй раз в точках, лежащих уже на прямой = − + 4, верхним пределом на 2 < ≤ 4 будет 22 ( ) ≡ = − + 4.
Итак, область пришлось разбить на две части:
1 2
Тогда интеграл будет иметь вид:
( , ) = ( , ) + ( , ) =
|
1 |
|
|
2 |
|
|
|
|
|
2 |
2 |
( ) |
|
4 |
2 ( ) |
||
|
|
|
1 |
|
|
2 |
|
|
|
= ∫ ∫ |
|
( , ) + ∫ ∫ |
( , ) = |
||||
|
0 |
1( ) |
|
2 |
1( ) |
|
|
|
|
2 |
|
|
4 |
− +4 |
|
16 |
|
|
= ∫ ∫ + ∫ ∫ |
= |
||||||
|
|
|
||||||
|
3 |
|
||||||
|
0 |
0 |
|
2 |
0 |
|
|
|
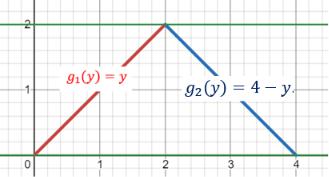
V.Теперь «зажмем» область прямыми = 0 и = 2. Тогда нижняя граница (точка «входа», если двигаться вдоль оси 0 из минус бесконечности) 1( ) ≡ = , а верхняя
(точка «выхода») - 2( ) ≡ = 4 − .
Интеграл будет иметь вид:
|
2 |
2( ) |
2 |
4− |
|
16 |
|
(, ) = ∫ |
∫ |
(, ) = ∫ |
∫ |
= |
|||
|
|||||||
3 |
|||||||
|
0 |
1( ) |
0 |
|
|
|
|
|
|
|
|
|
|
||
Обратите внимание: в данном случае область не пришлось разбивать на две, что существенно упростило расстановку пределов и в дальнейшем существенно упростило расчёты (см замечание f)
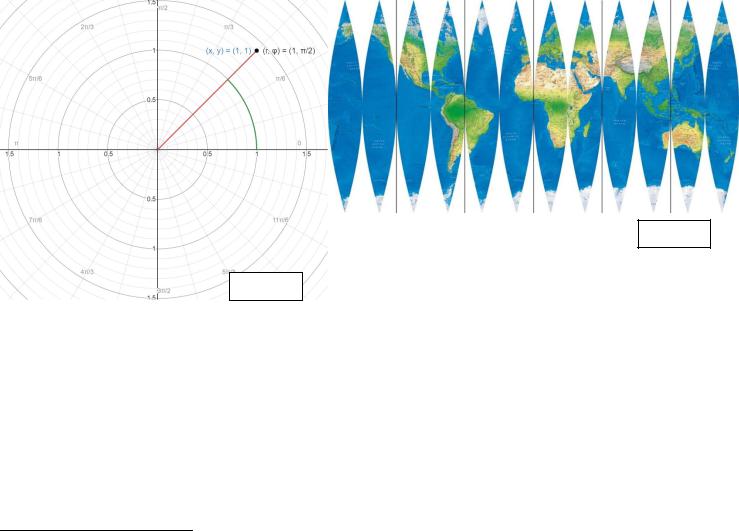
Немного про системы координат.
1) Декартова система координат
Положение точки в пространстве определяется двумя координатами: координатой по оси и координатой по оси .
2) Полярная система координат.
Положение точки в пространстве определяется расстоянием до нее от центра координат и углом между радиус-вектором в эту точку и ортом (осью 0 ). (рис A)
Из определения понятно, что |
|
|
0 |
≤ |
(Расстояние неотрицательно) |
{0 |
≤ ≤ 2 (Все возможные углы лежат в этом промежутке) |
|
Нетрудно показать, что формулы перехода между декартовыми и полярными системами координат имеют вид:
{ |
= ( ) |
, (, ) = |
(3)2 |
= ( ) |
При смене системы координат происходит деформация пространства, при которой площади и объемы тел могут меняться. Например, изобразить поверхность земли на плоской карте без потери пропорций не так уж и просто (рис. B)
Рис. B
Рис. А
Когда производится замена переменных (или, в частности, переход к полярной системе координат), вводится некоторая функция, которая позволяет получать одинаковый результат в разных системах.
Без лишней теории покажу, как считать эту функцию, называемую якобианом.
Пусть интегрируемая функция (, ), а область интегрирования .
2 Про якобиан будет написано позднее, здесь он указан для общности.

Произведем замену переменных3 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
{ = ( , ), → |
|
|
|
|||||||||||
|
|
= ( , ) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
( , ) = det ( |
) ≠ 0 |
(4)4 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(, ) = ((, ), (, )) ∙ |( , )| (5) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Полезный факт: (, ) = |
1 |
, то есть якобиан замены равен выражению, обратному якобиану |
||||||||||||||
(, ) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
обратной замены: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
( , ) = det ( |
|
) = det |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
[ |
( |
|
)] |
|||||||
Пример 2 (переход в полярную систему координат):
Пусть интегрируемая функция (, ), область интегрирования (это может быть любая замкнутая кривая на плоскости. Вспомните, Александр Владимирович давал нам уши слона, треугольники, прямоугольники и т. п.). Произведем полярную замену (то есть перейдем к полярной системе координат):
= ( ) { = ( )
Тогда функция примет вид ( ( ), ( )) – просто вместо x и y подставляем новые выражения из системы выше. Важно: если область тоже задана как функция (, ), то и в ней необходимо произвести замену. Например, если область была (, ) ≡ 2 + 2 = 1, то (, ) ≡
(( ))2 + (( ))2 = 2 = 1, или,с учетом того, что ≥ 0, (, ) ≡ = 1.
Посчитаем якобиан замены:
|
|
( ( )) |
|
(( )) |
|
|
|
|
|
|
|
(, ) = det |
|
|
|
|
= ( ) cos( ) + ( ) sin( ) = > 0 5 |
|
(( )) |
|
( ( )) |
||
|
|
|
|
||
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
|
|
||
Теперь, используя формулу (5) выводим: |
|
||||
|
|
(, ) = (( ), ( )) (6) |
|||
|
|
|
|
|
|
3Ради простоты я не упоминаю, важный факт: пусть после замены переменных область интегрирования переходит в область . Тогда функции и должны иметь непрерывные частные производные 1-го порядка в области . Иначе,
замена некорректна.
4Якобиан замены невырожден, если получился 0 – такую замену делать нельзя
5Поскольку якобиан не должен быть тождественно равен нулю, точка = 0 не портит картину.
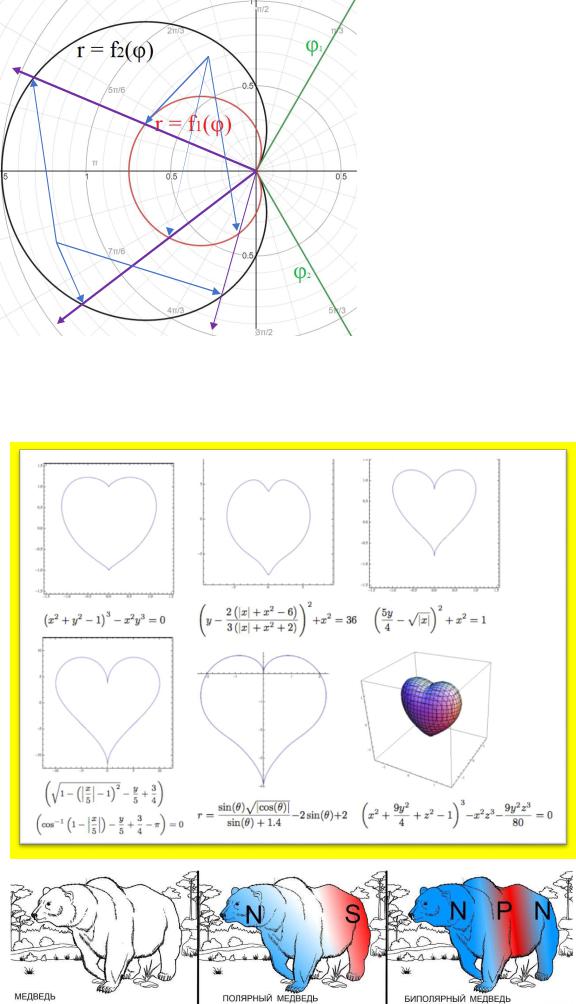
Для того, чтобы расставить пределы
|
интегрирования в полярной системе координат, |
|
|
поступают так же, как и в декартовой, только |
|
«вход» |
||
«зажимают» область крайними углами, а |
||
|
||
|
||
|
уравнения верхнего и нижнего пределов |
|
|
выражают как функции от : |
|
В данном примере { 1( ) ≤ ≤ 2( ) |
|||
|
|
≤ ≤ |
2 |
|
|
1 |
|
||
|
То есть смотрим, в каких точках всевозможные |
|||
|
радиус-векторы пересекают : уравнением |
|||
«выход» |
||||
«входа» будет = 1( ), |
уравнением «выхода» - |
|||
|
||||
|
||||
|
2( ). |
|
|
|
|
Соответственно, пользуясь формулой |
|||
|
расстановки пределов в полярной системе |
|||
|
координат, получаем |
|
|
|
|
|
2 |
|
2( ) |
(, ) = (( ), ( )) = ∫ |
∫ |
(( ), ()) |
||
|
|
1 |
1( ) |
|
Просто чтобы не оставлять пустой половину страницы:
Пример 3 (обобщение и демонстрация расстановки пределов в полярной системе координат):
Вычислить
, где : 2 − 4 + 2 > 0, |
2 − 8 + 2 < 0, |
> |
|
, > 0 |
||
|
|
|||||
√3 |
||||||
|
|
|
||||
|
|
|
|
|
|
|
Страшно, да?
Решение:
Когда видим уравнение с квадратами обеих переменных, у нас в голове загорается лампочка: скорее всего, где-то тут окружность неподалёку, может быть будет удобно перейти к полярной системе координат.
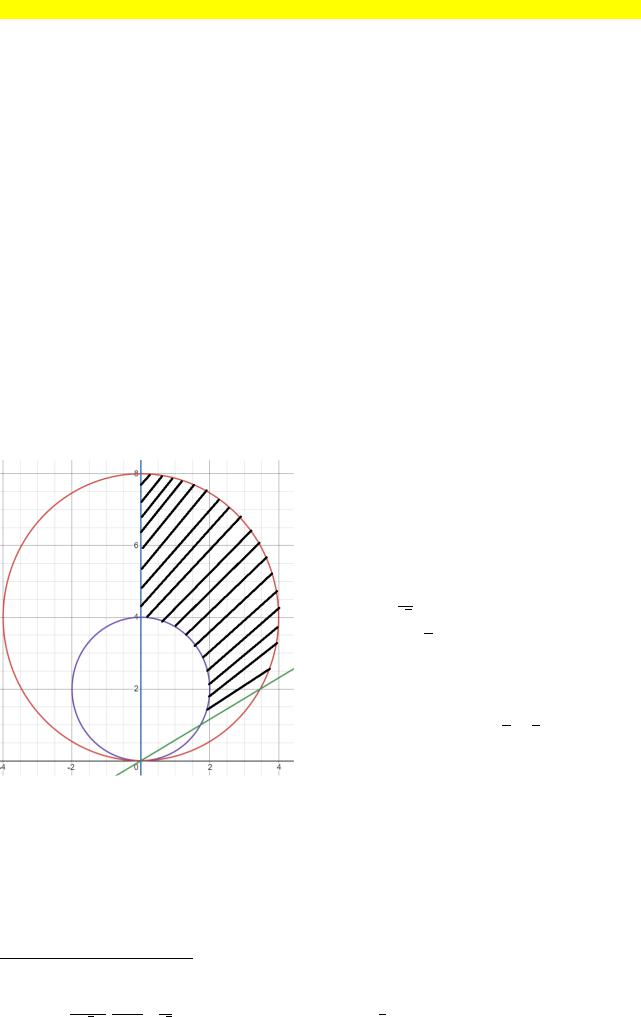
Для начала преобразуем и построим область .
2 − 4 + 2 = 2 + ( − 2)2 − 4 > 0
−то есть область вне окружности,с центром (0,2) и радиусом 2
2 − 8 + 2 = 2 + ( − 4)2 − 16 < 0
−то есть область внутри окружности, с центром (0, 4) и радиусом 4.
Оставшиеся два уравнения представляют из себя прямые.
Построим область:
Сразу перейдем к полярной системе координат:
Окружность с центром в (0, 2) и радиусом 2 имеет уравнение6 = 4sin( )
Окружность с центром в (0, 4) и радиусом 4 имеет уравнение7 = 8sin( )
Прямая = в полянах координатах имеет
√3
уравнение8 = 6
Уравнение же интегрируемой функции ( , ) примет вид ( ( ), ( )) = ( )
«Зажмем» между углами 6 и 2 : ясно, что радиус будет меняться от 4 sin( ) до 8sin( )
Тогда
|
|
|
8sin( ) |
|
|
|
2 |
|
|
|
|
∫ |
( ) 2 = 35 |
|
( , ) = ( ( ), ( )) = ∫ |
||||
|
|
|
4 sin( ) |
|
|
|
6 |
|
|
|
|
|||
*простите, не хочется сюда выписывать все решение, и так объем немаленький
6( ( ))2 − 4 ( ) + ( ( ))2 = 0 ↔ = 4sin( ): просто в уравнения подставляем полярную замену
7Аналогично сноске 6, только вместо «4» - «8».
8( ) = √3( ) , cos(sin( )) = √31 → уравнение принимает вид = 6 в силу того, что [0,2 ]
