12. Перестановки с повторениями. Число разбиений конечного множества на подмножества

Пусть множество A с n элементами содержит повторяющиеся элементы m типов. Например, множество цифр числа 732773 содержит элементы трёх типов {7;3;2}. Обозначим через k_i число элементов i-го типа, i=1, …,m, k₁+…+k_m= n. Сколько можно получить различных перестановок элементов множества А? Перестановка повторяющихся элементов не приводит к новым перестановкам. Поэтому число перестановок элементов множества с повторяющимися элементами будет равно

Пусть А конечное множество, 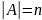. Зададим целые положительные числа k₁, …, k_m такие, что

Теорема

Число разбиений множества А на m непересекающихся подмножеств

равно

Доказательство

Сначала построим первое подмножество как неупорядоченную (n, k₁)-выборку без повторений. Это можно сделать способами.

Затем построим второе подмножество. Для этого необходимо выбрать k₂ элементов из оставшихся n-k₁. Это можно сделать способами.

И так далее, пока не останутся последние k_m элементов.

По правилу произведений получим:

13. Биномиальные коэффициенты и их свойства. Треугольник Паскаля

Числа называются биномиальными коэффициентами

Справедливы формулы:

1. 

2. 

3. 

4. 

Доказательство:

Докажем 3 свойство. Сумма коэффициентов

Формулу можно использовать для последовательного вычисления биномиальных коэффициентов. Результаты вычислений образуют треугольник Паскаля

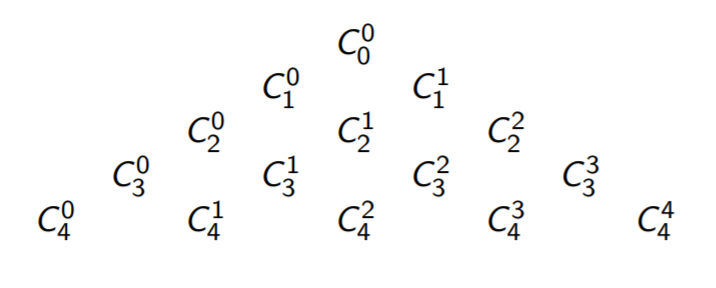
Каждый из внутренних элементов треугольника равен сумме двух элементов, расположенных над ним

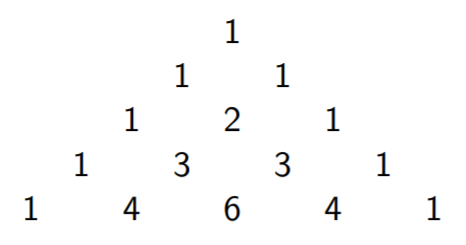
14. Полиноминальная формула. Бином Ньютона.

Полиномиальная формула

Бином Ньютона

Доказательство.

Рассматриваемое выражение запишем в виде произведения n скобок

При раскрытии скобок получим mⁿ слагаемых следующего вида , которые могут содержать повторяющиеся переменные. Пусть число повторений переменных 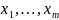равно соответственно 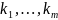. Тогда

Число таких слагаемых равно числу перестановок с повторениями

При m =2 полиномиальная формула принимает вид формулы бинома Ньютона.

Как следствие формулы бинома Ньютона получим

15. Метод включений и исключения.

Пусть А конечное множество и . Пусть заданы некоторые свойства элементов множества А. Обозначим число элементов множества А, обладающих свойствами через N( . Тогда число элементов множества А, не обладающих ни одним из свойств p₁, …, p_m, равно

Доказательство.

Обозначим через А_i подмножество элементов множества A, обладающих свойством p_i. Тогда есть подмножество элементов, которые не обладают свойством p_i. Пересечение этих подмножеств

есть подмножество элементов, которые не обладают ни одним из свойств

Из формулы включения-исключения следует

В этом соотношении

16. Задача о беспорядках

Рассмотрим множество . Беспорядком называется любая перестановка элементов множества А , в которой никакой из элементов не находится на своём месте, . Число беспорядков называют субфакториалом и обозначают !n

Теорема

Число беспорядков множества из n элементов равно

Число беспорядков можно определить, применяя метод включений и исключений. Обозначим через p_i свойство перестановки – элемент a_i расположен на своём месте. Тогда

Следовательно

Искомое значение субфакториала

Всего различных перестановок n!. Согласно методу включений и исключений

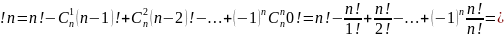
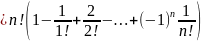
Для субфакториала справедливо рекуррентное соотношение

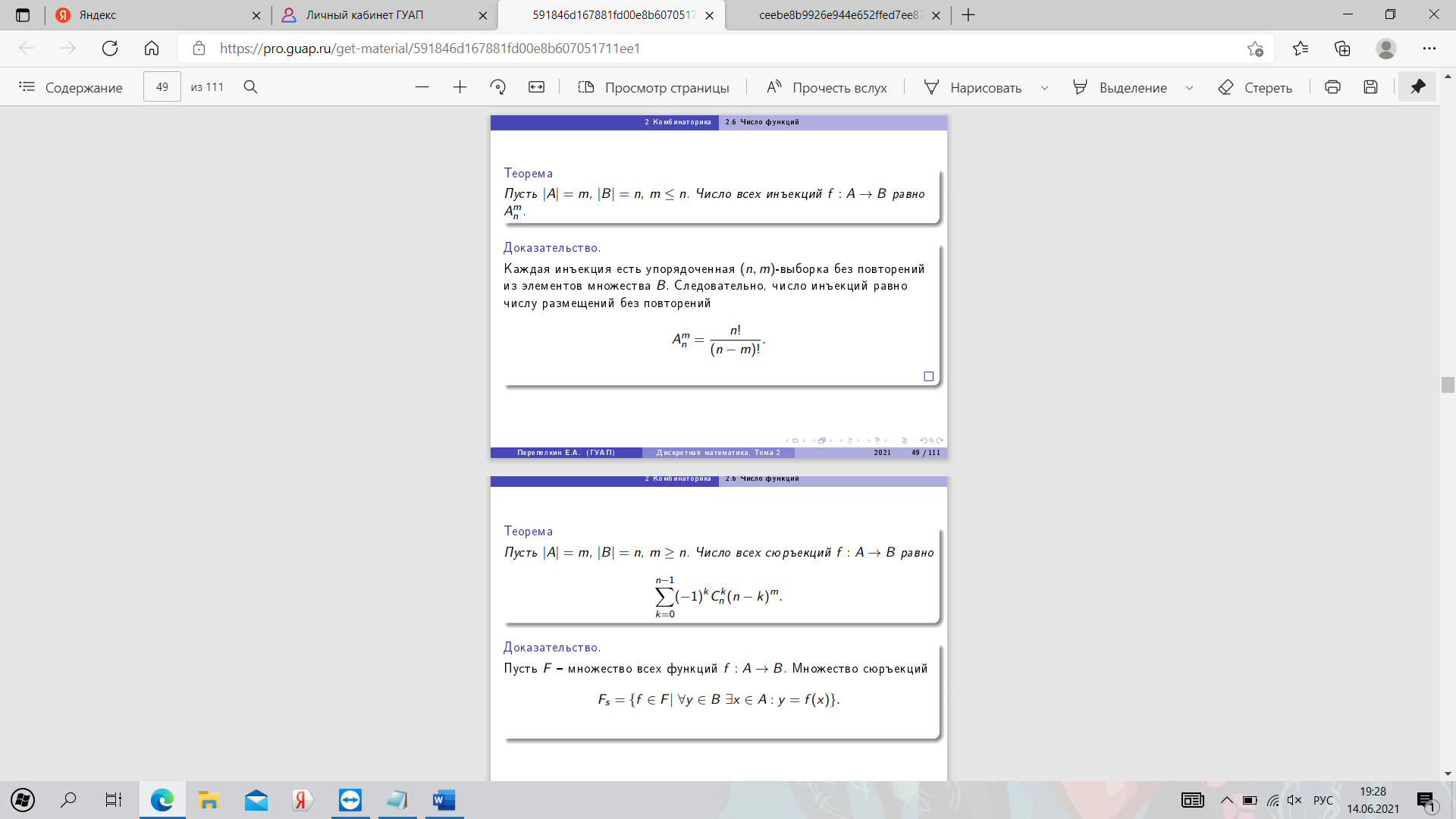
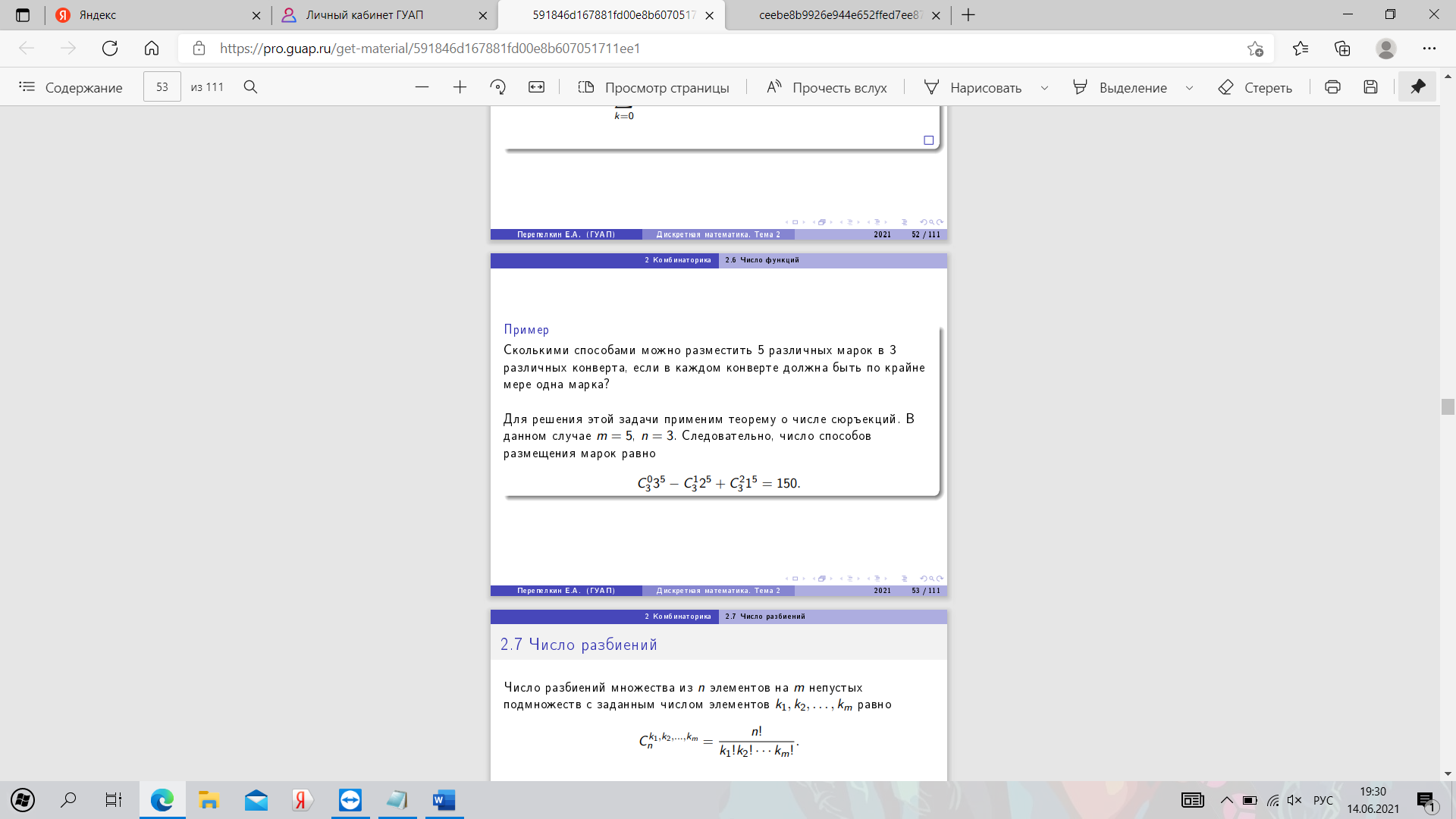
17. Число функций, биекций, сюръекций

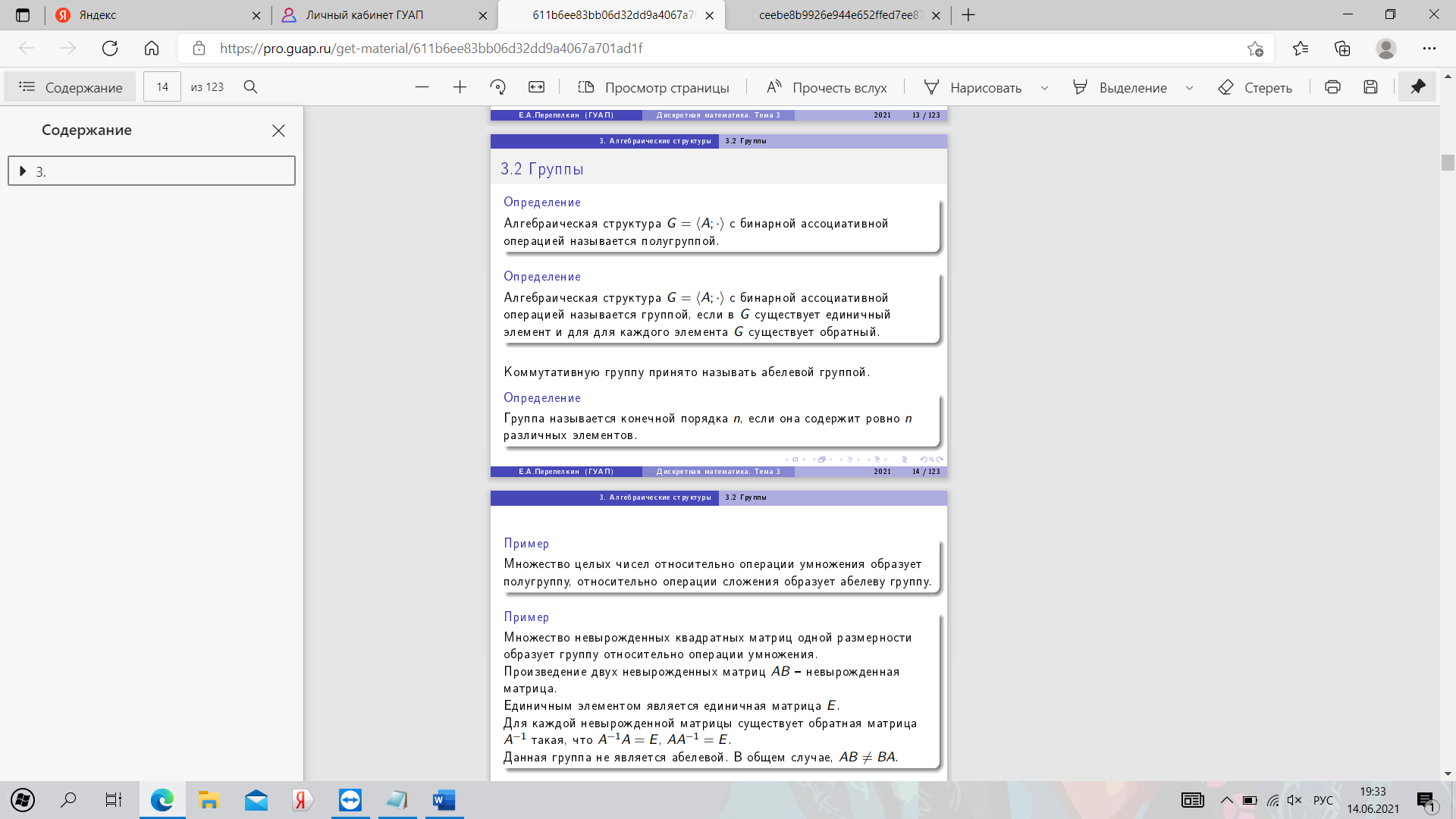
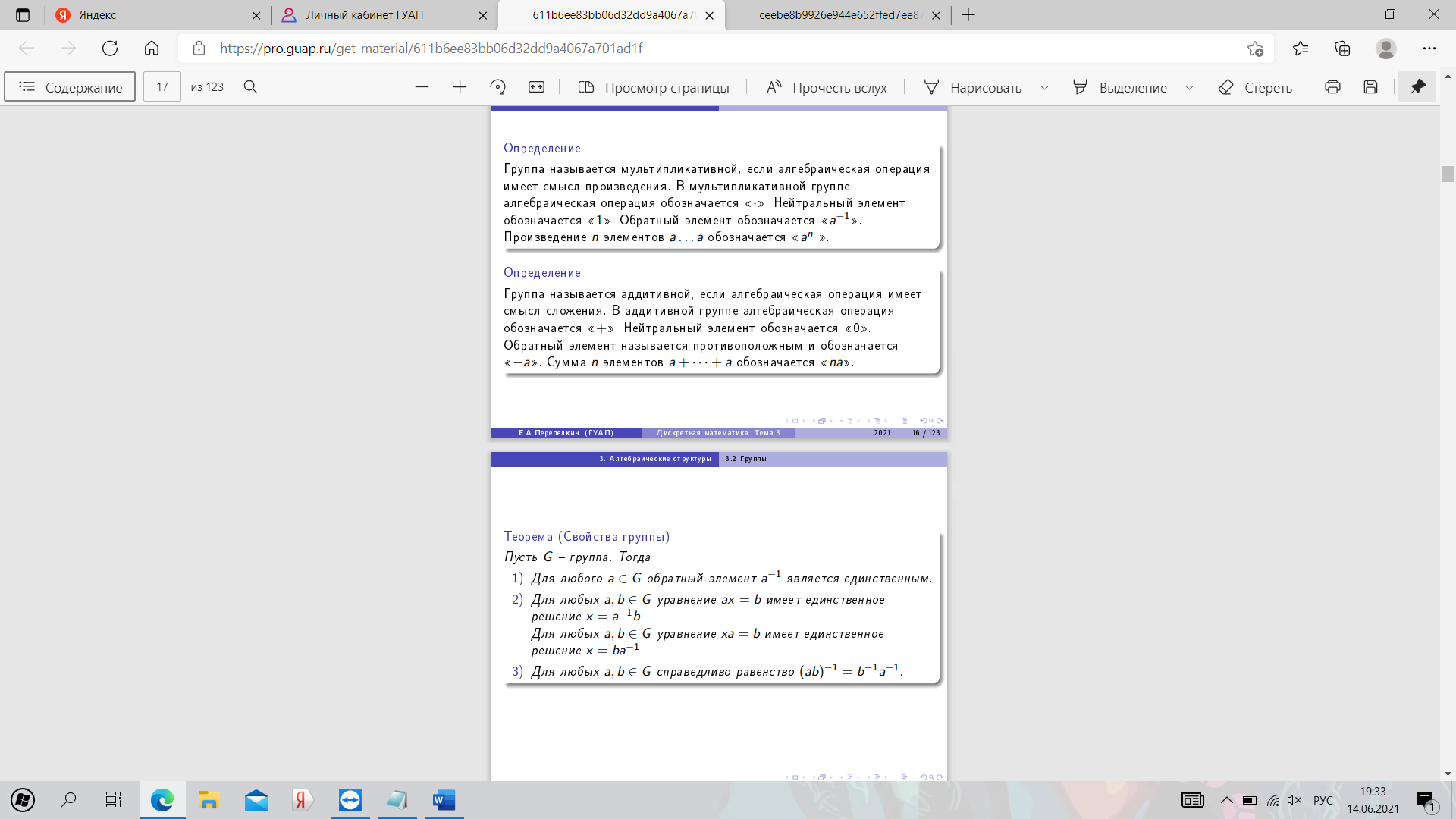
18. Определение и свойства групп

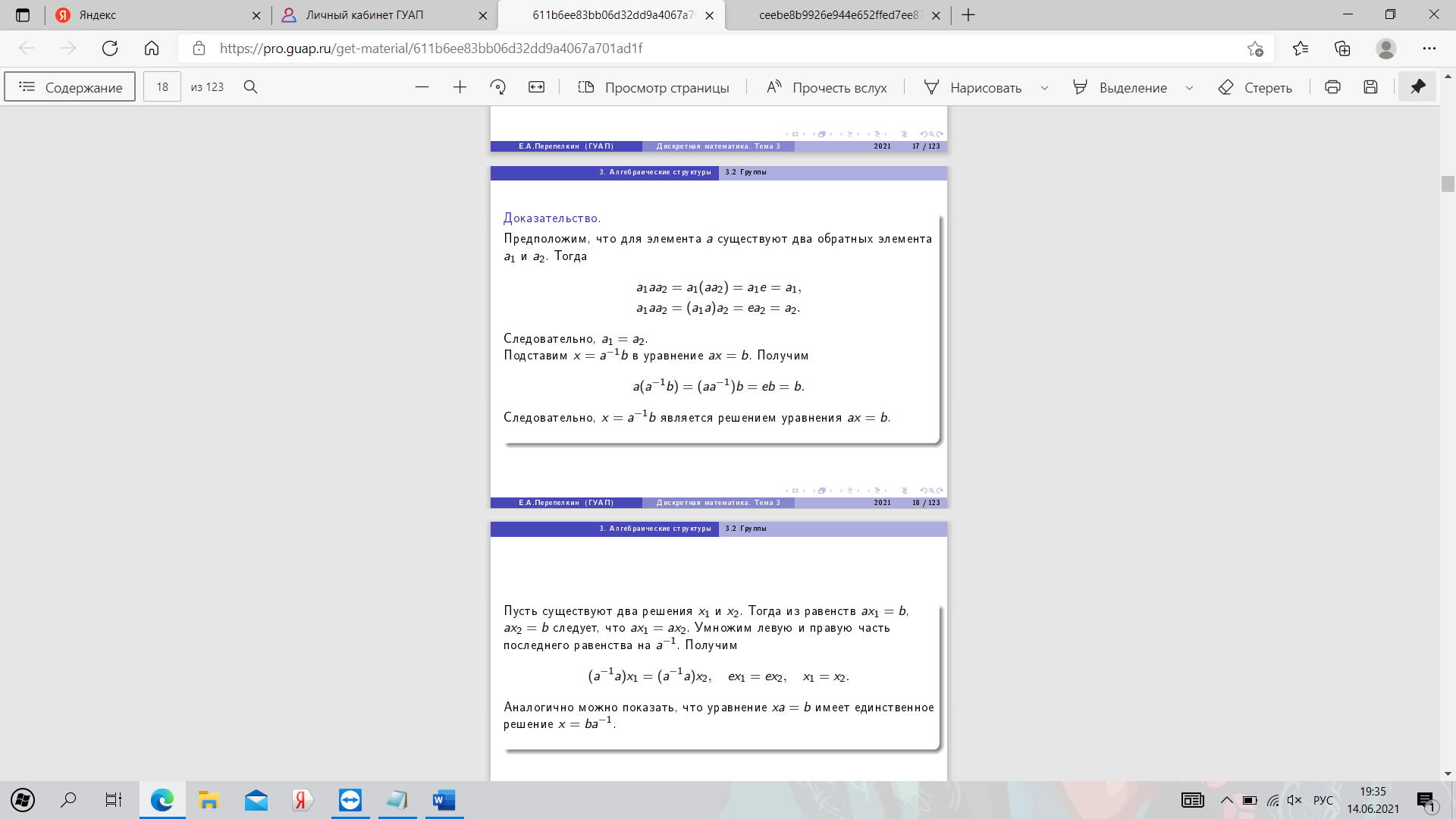
19. Порядок элемента группы. Теорема о циклической подгруппе.

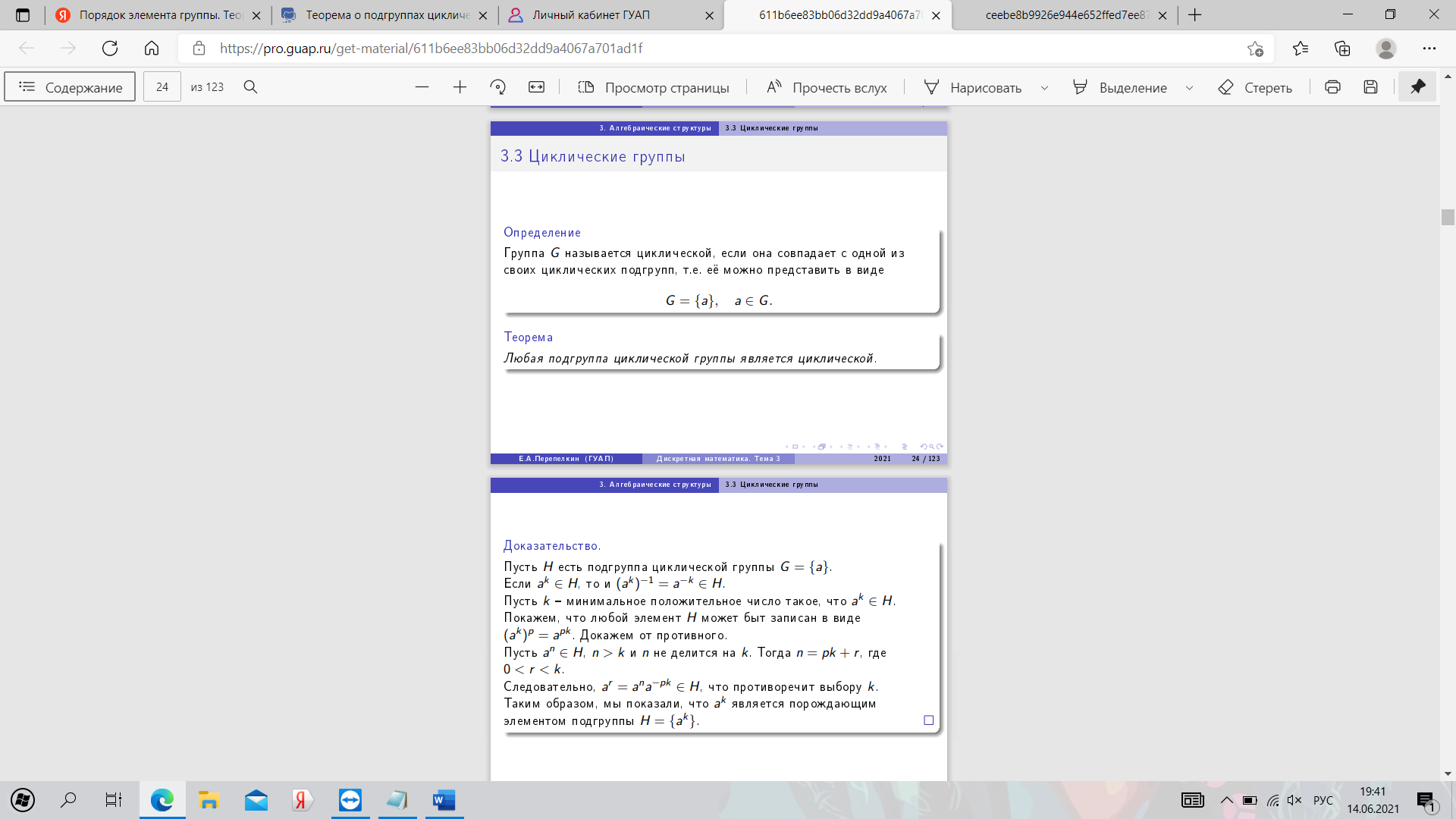
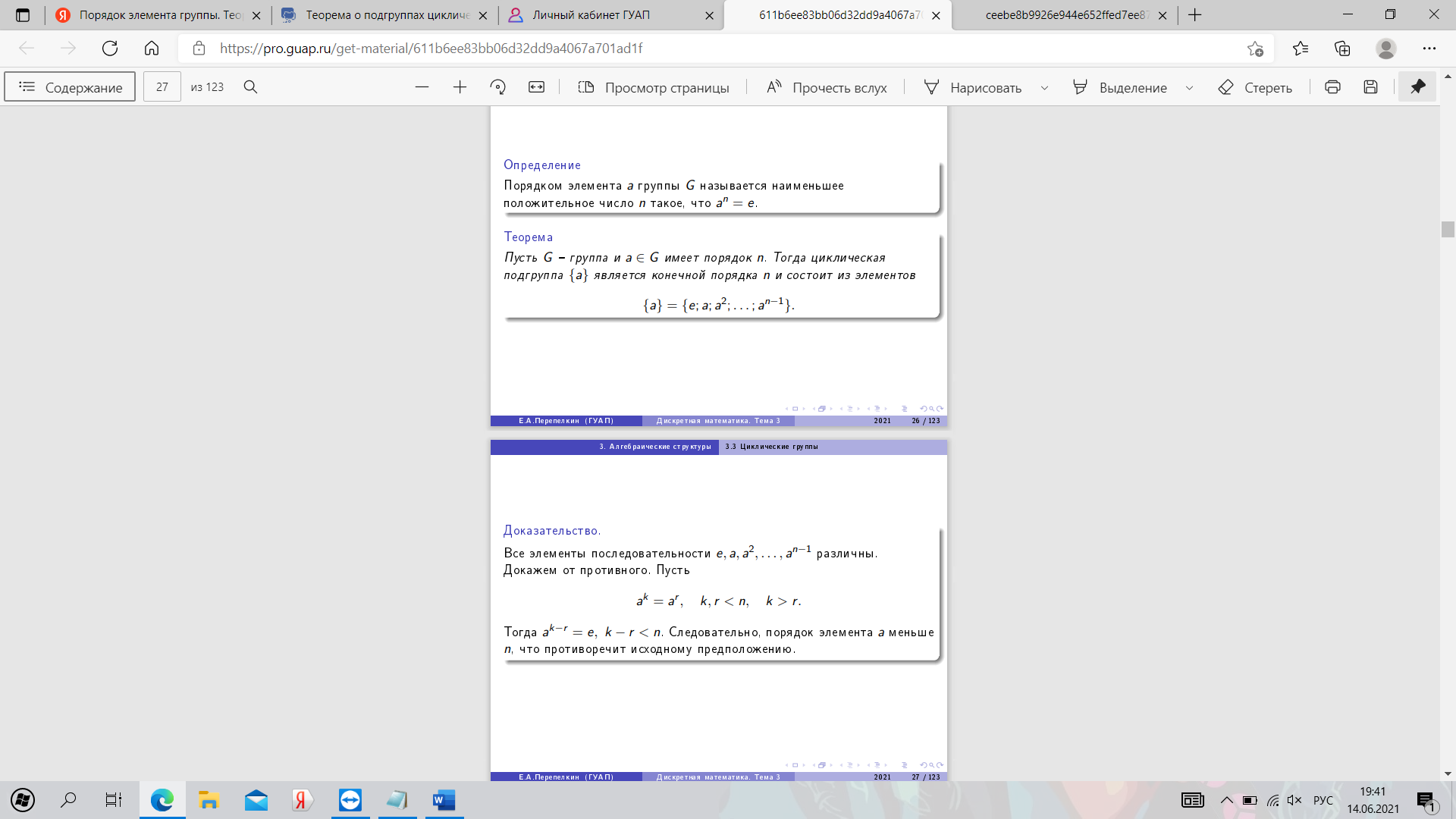
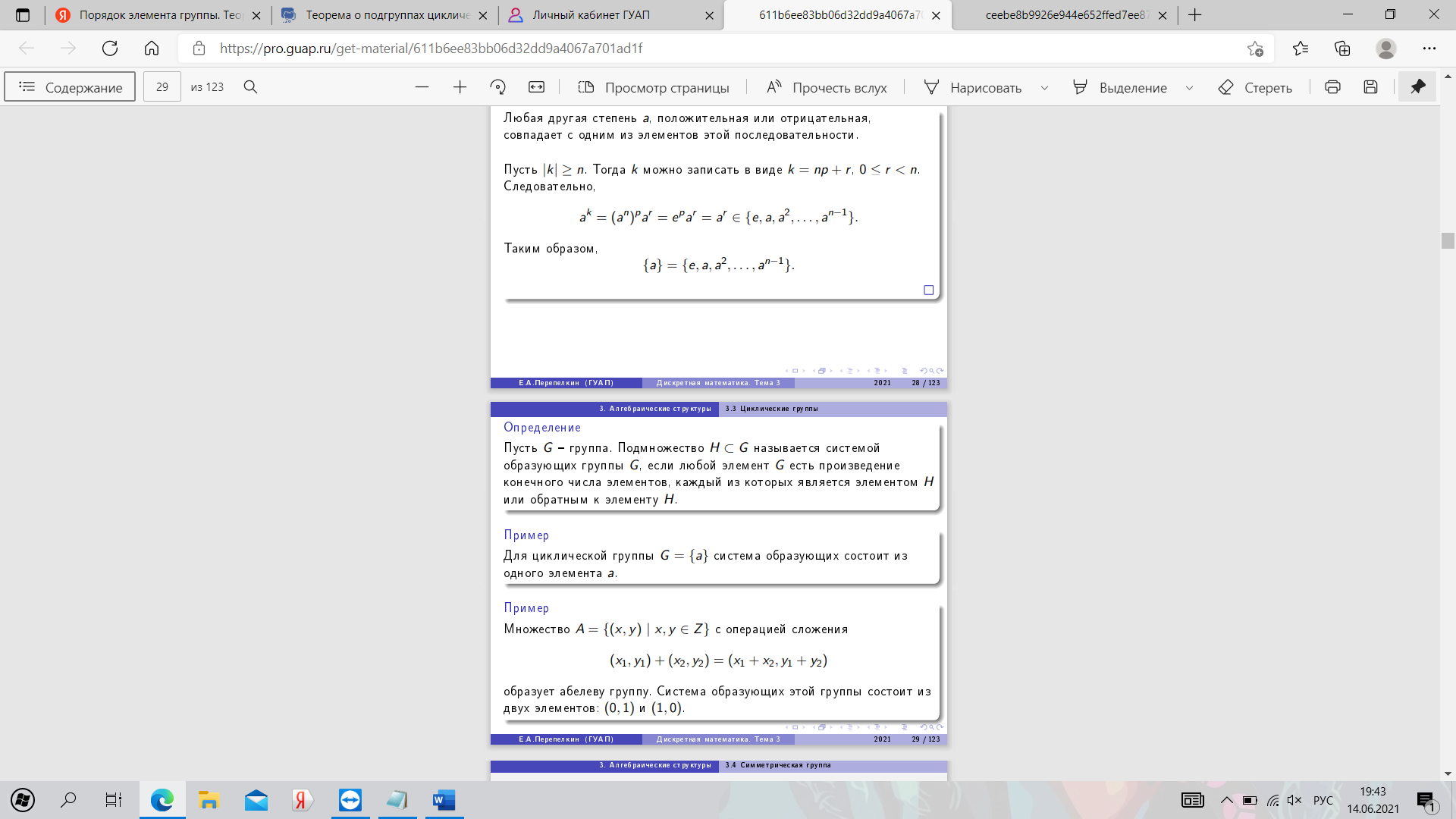
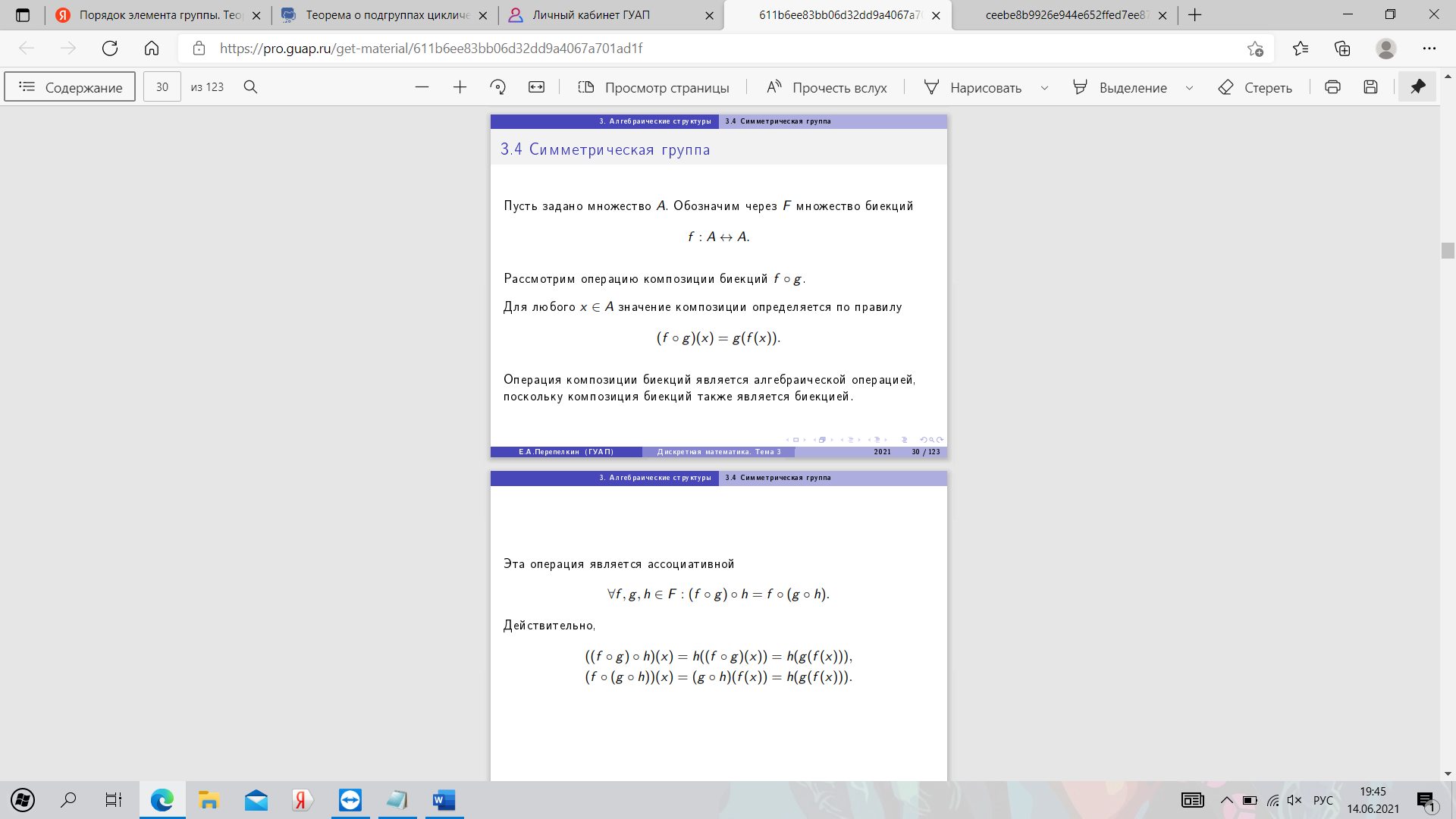
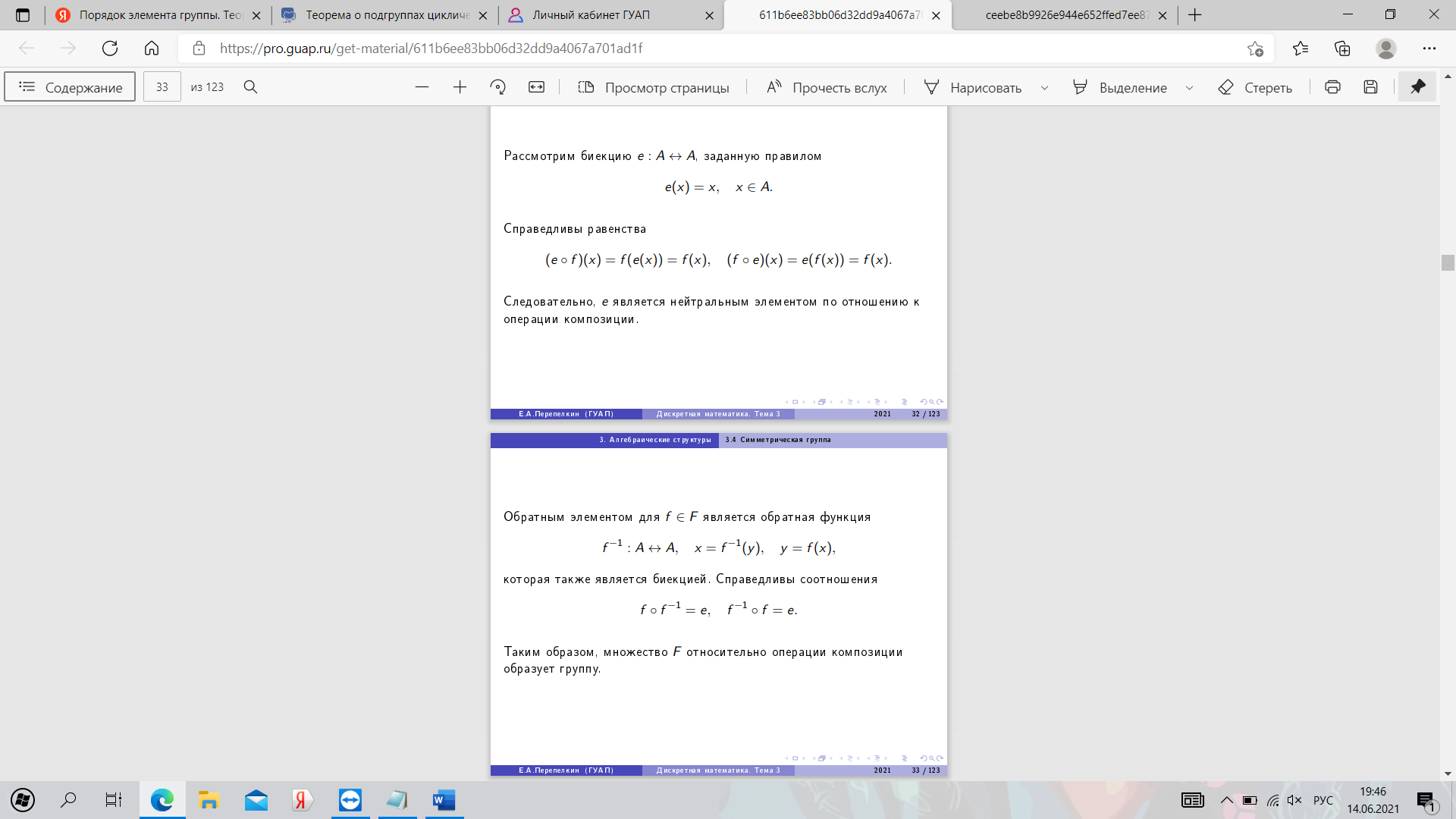
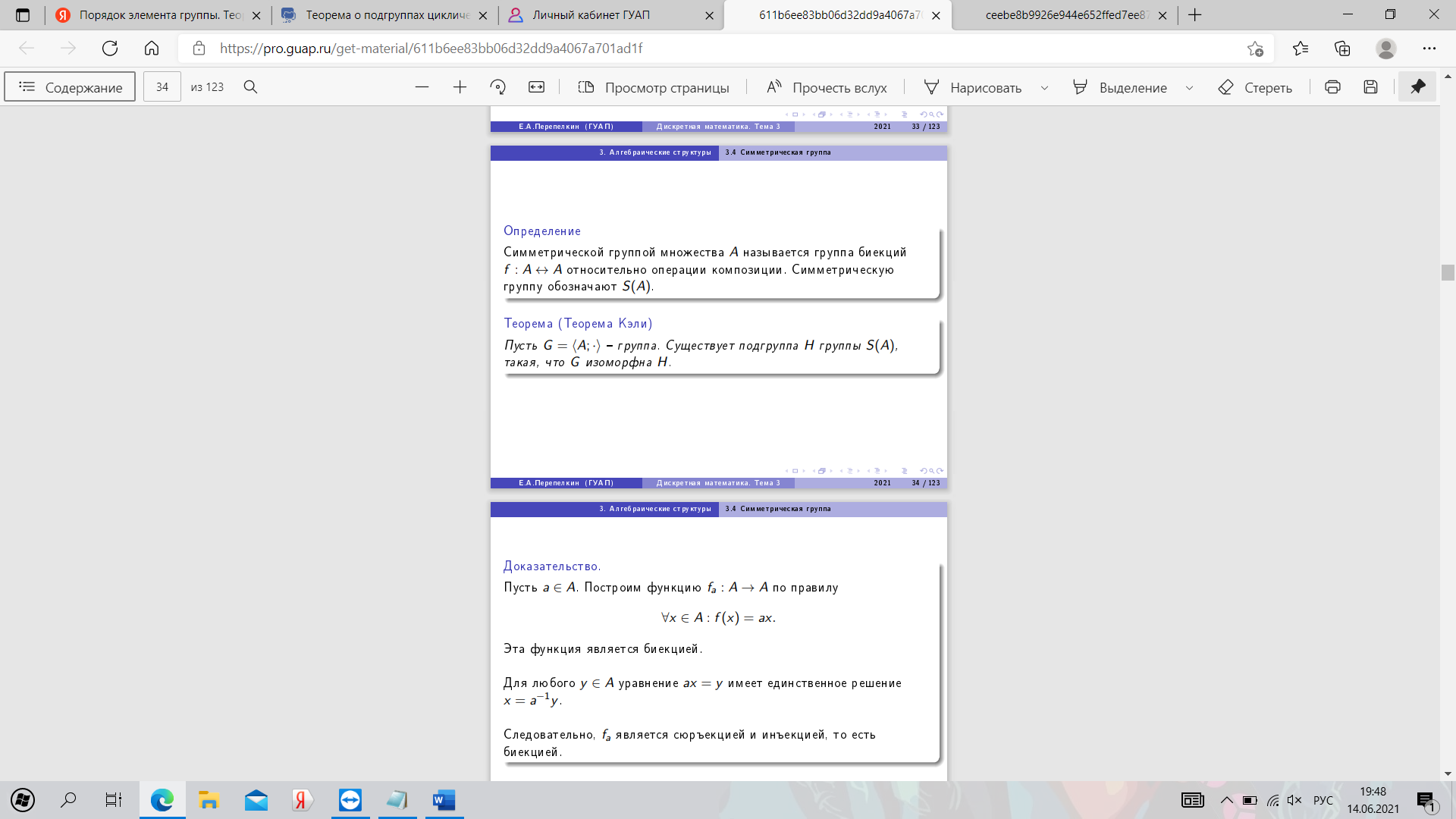
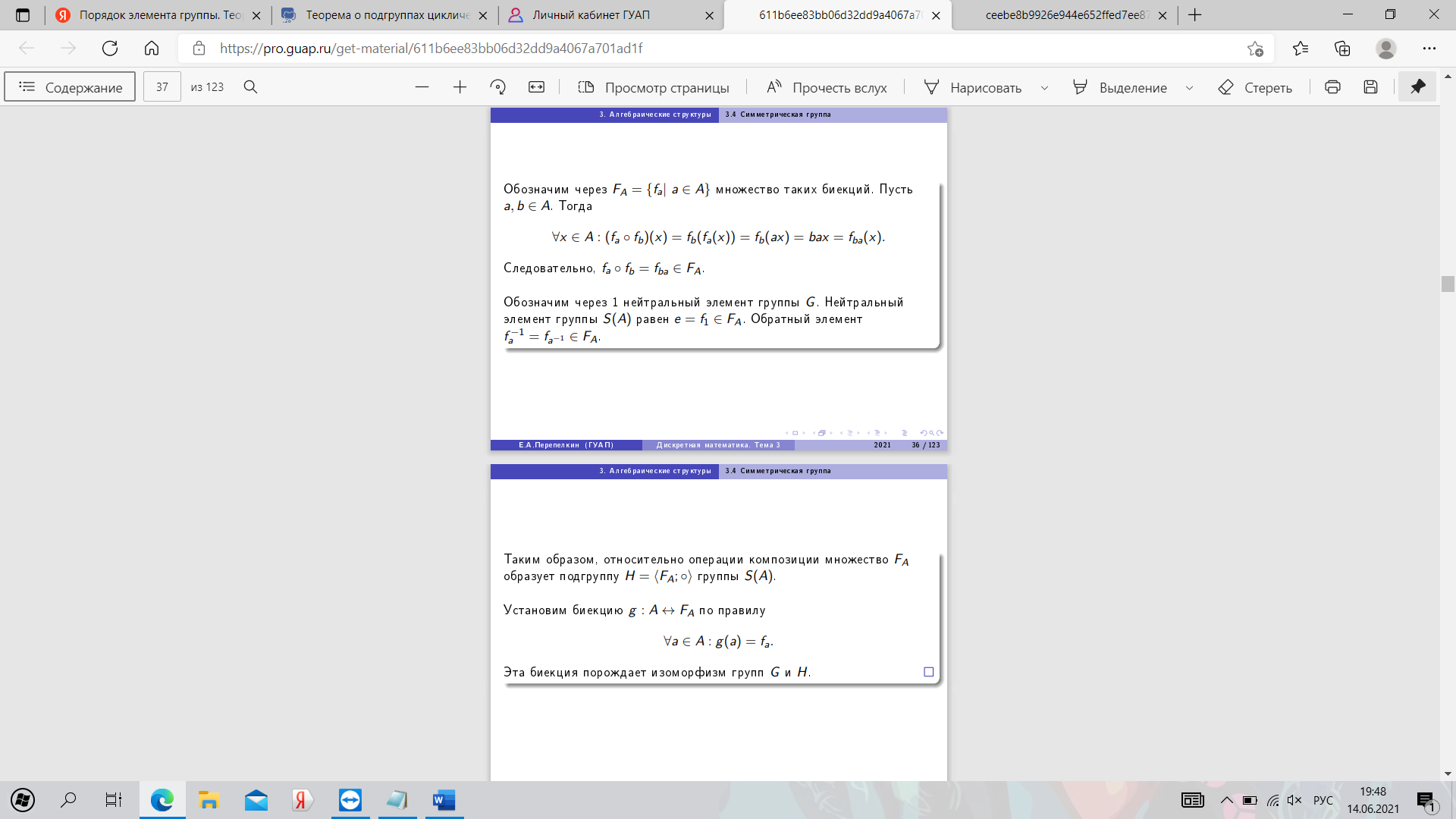
20. Симметрическая группа. Теорема Кэли.

21. Группа симметрий (группа подстановок).

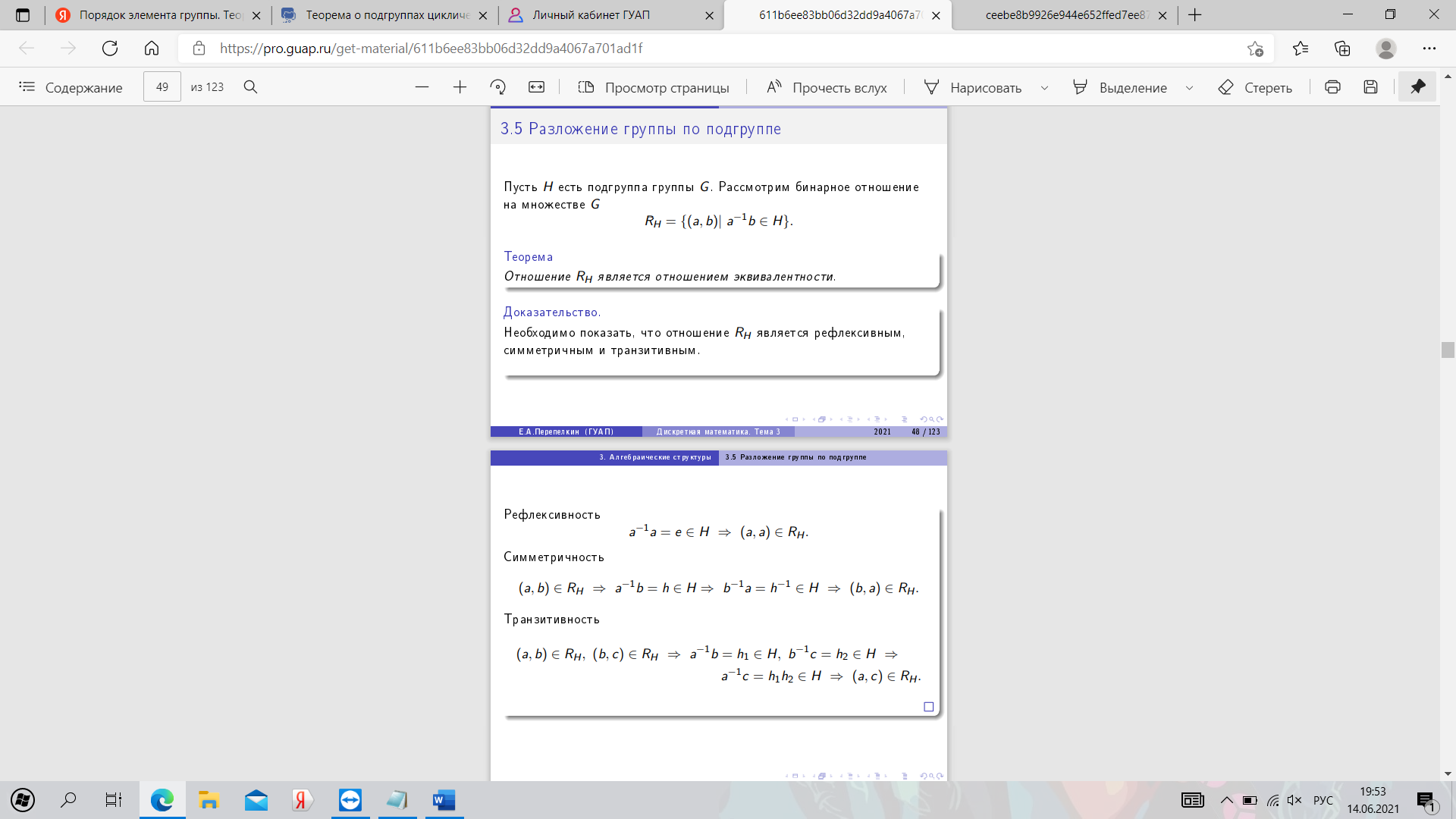
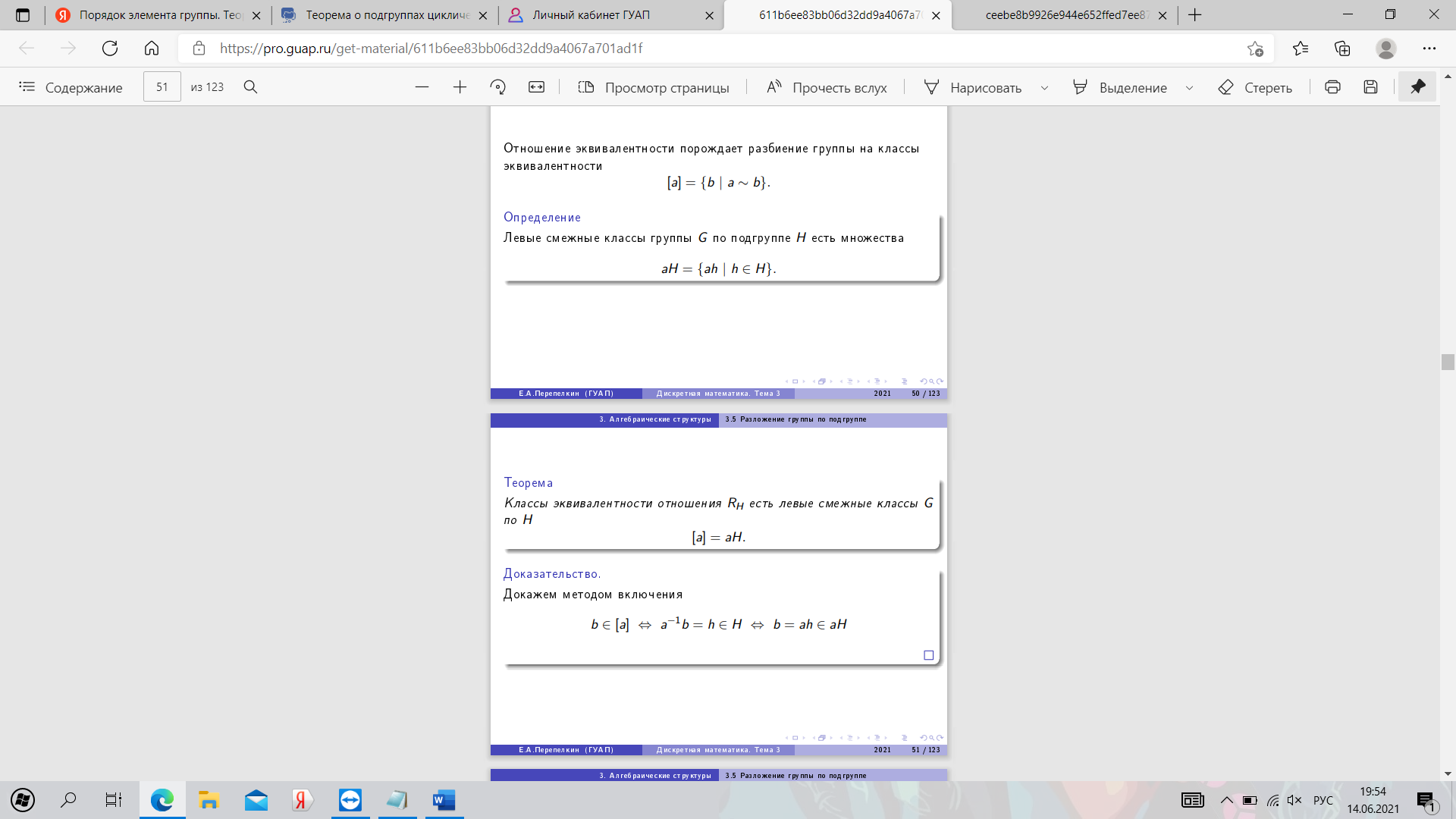
22. Разложение группы по подгруппе. Теорема Лагранжа.

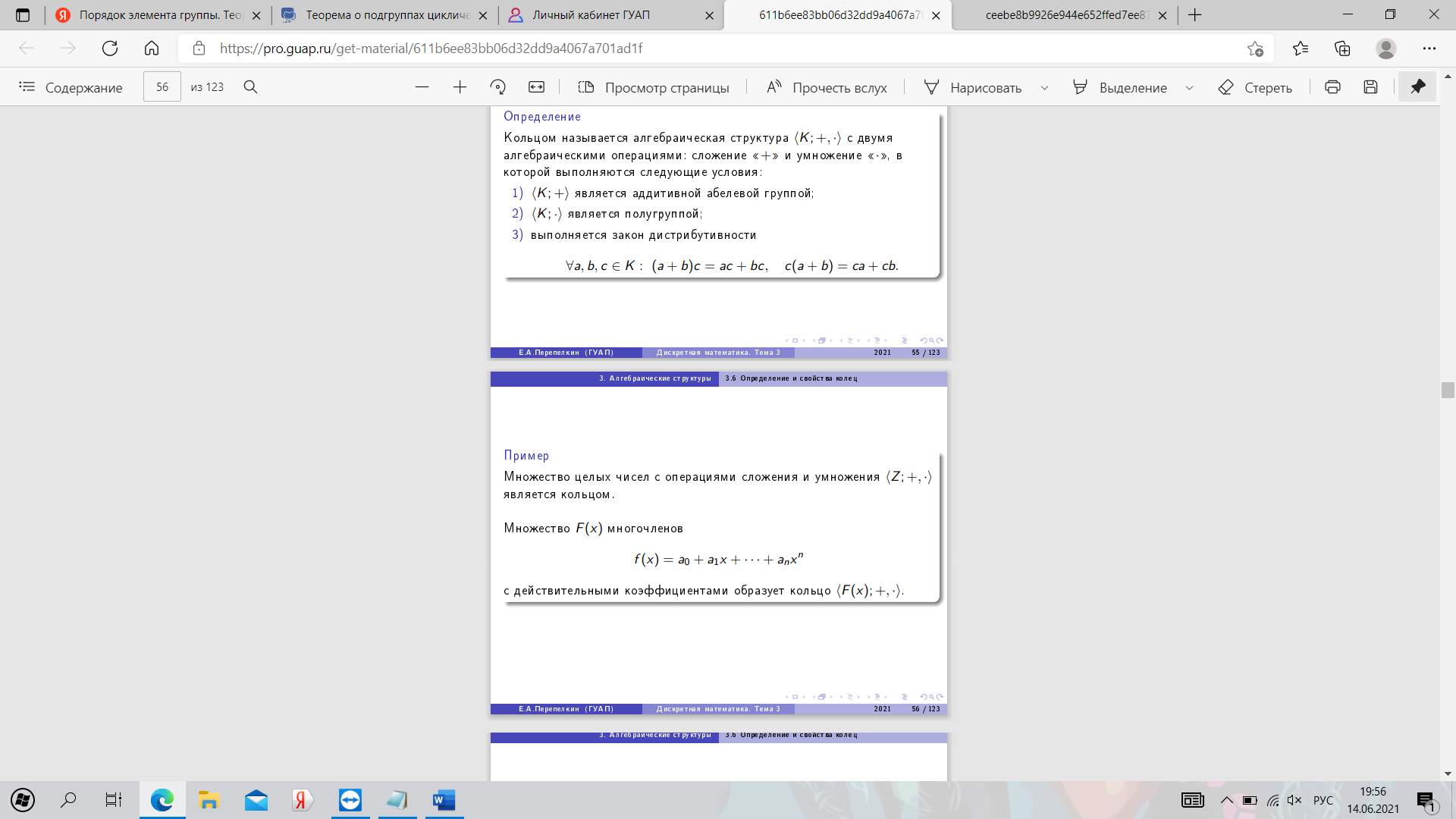
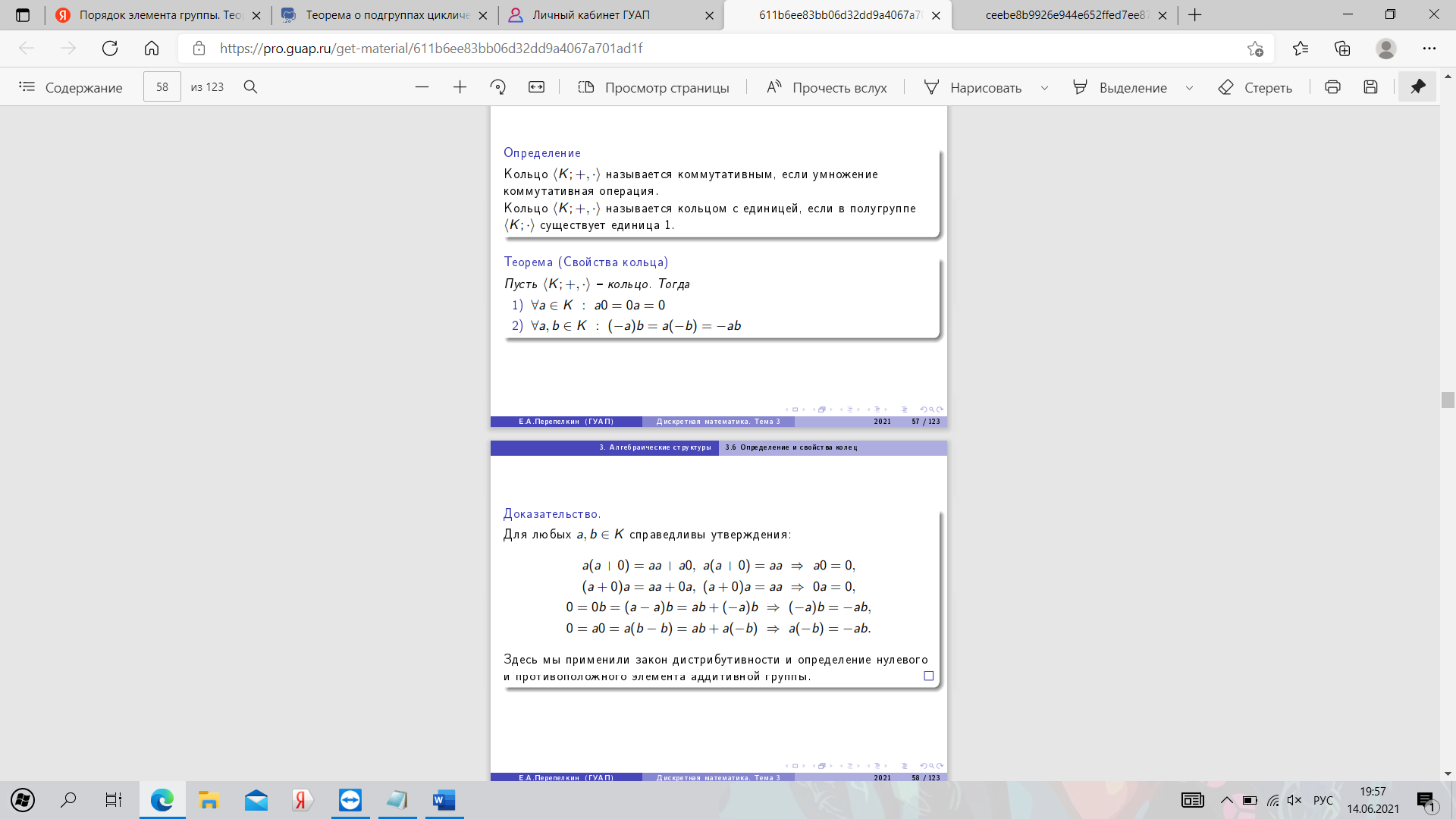
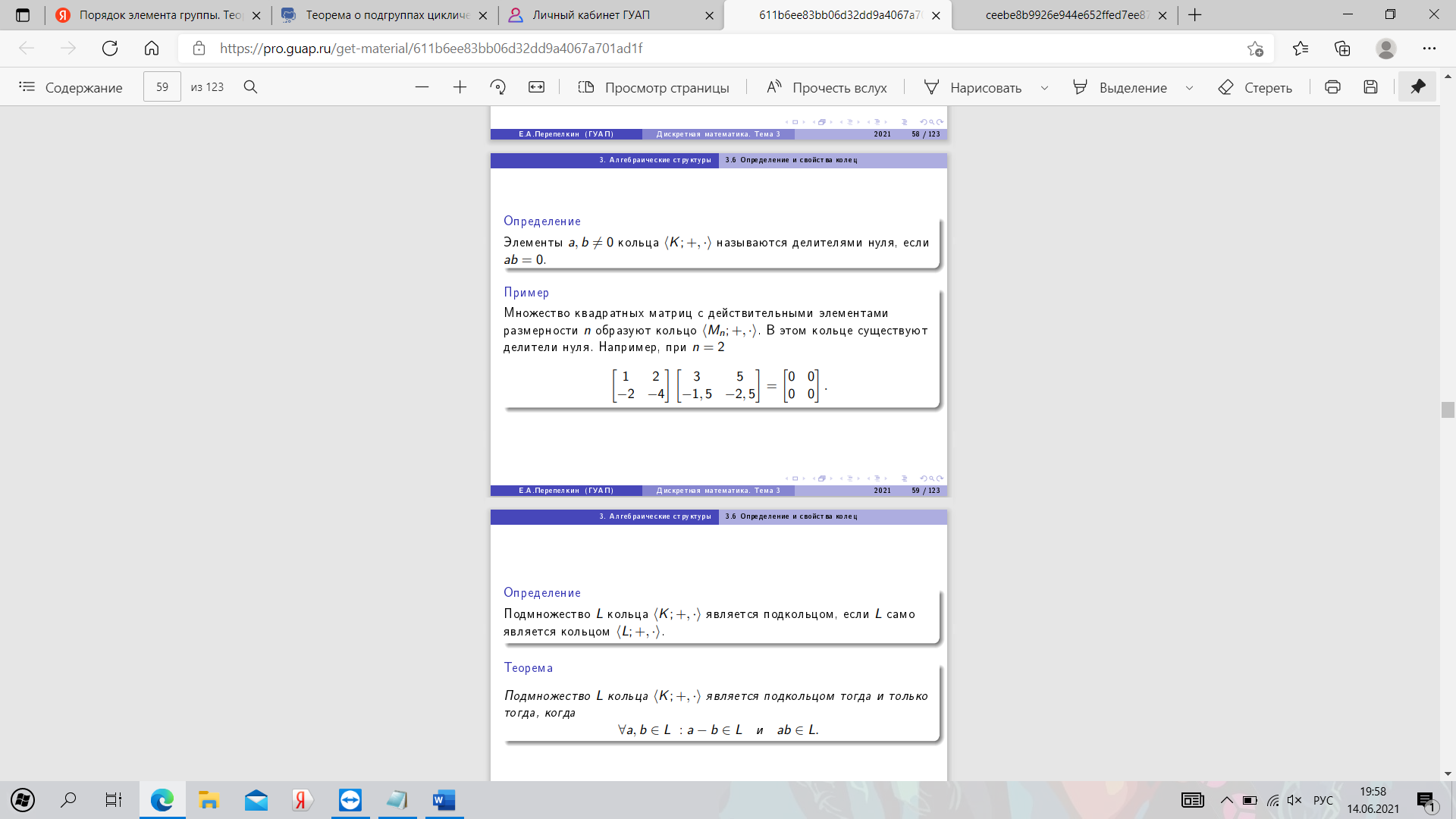
23. Определение и свойства колец.

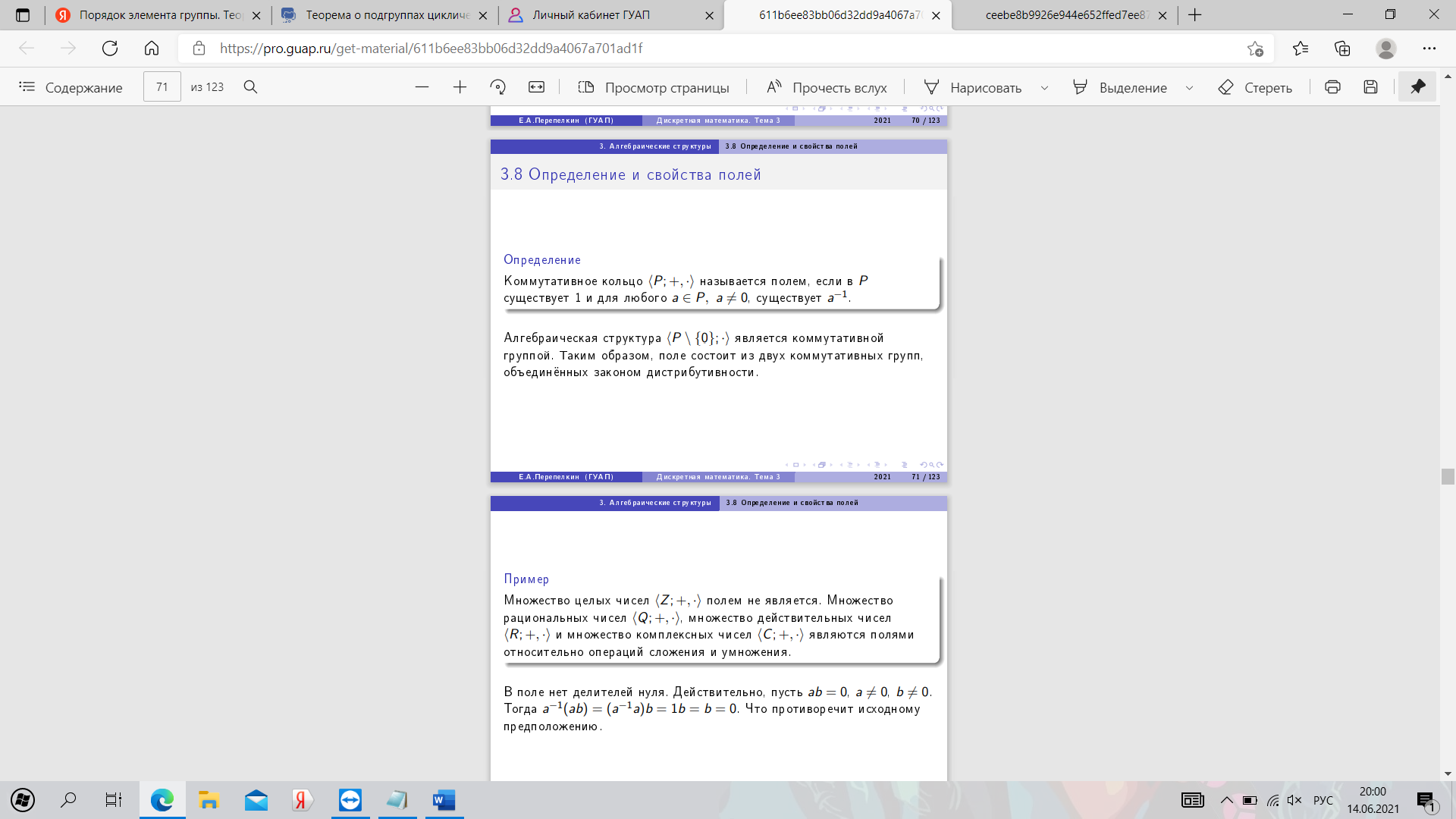
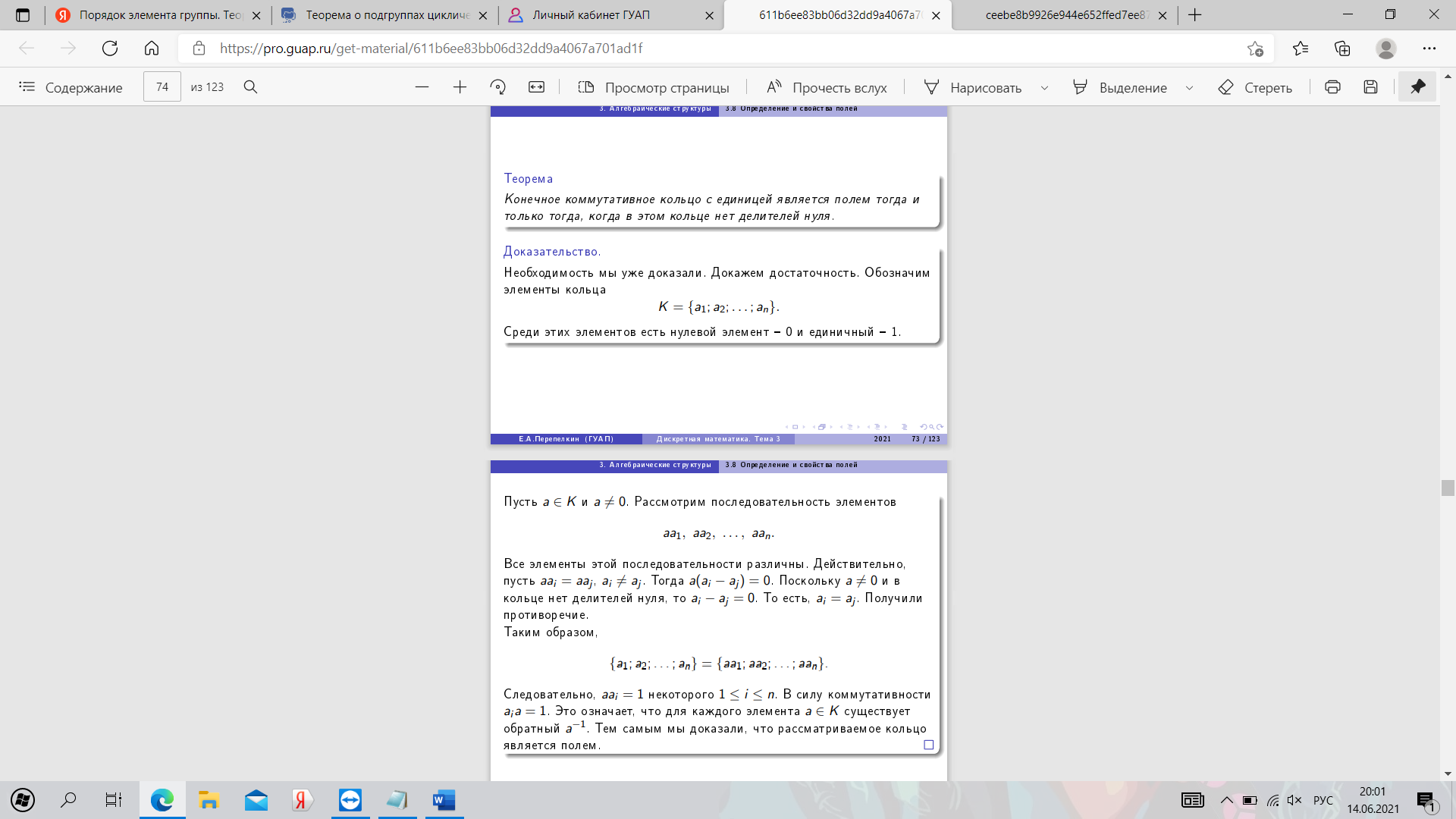
24. Определение и свойства полей

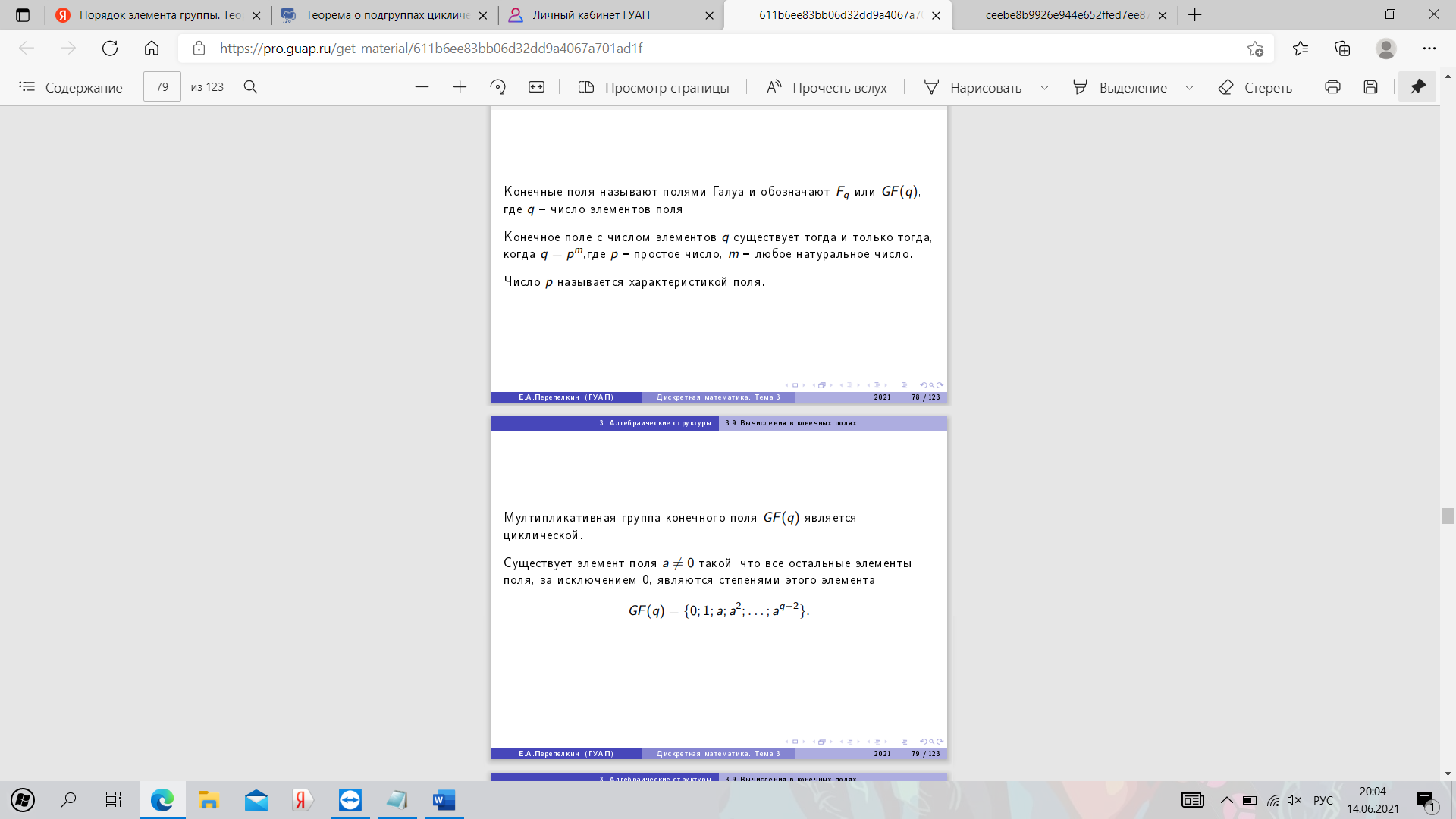
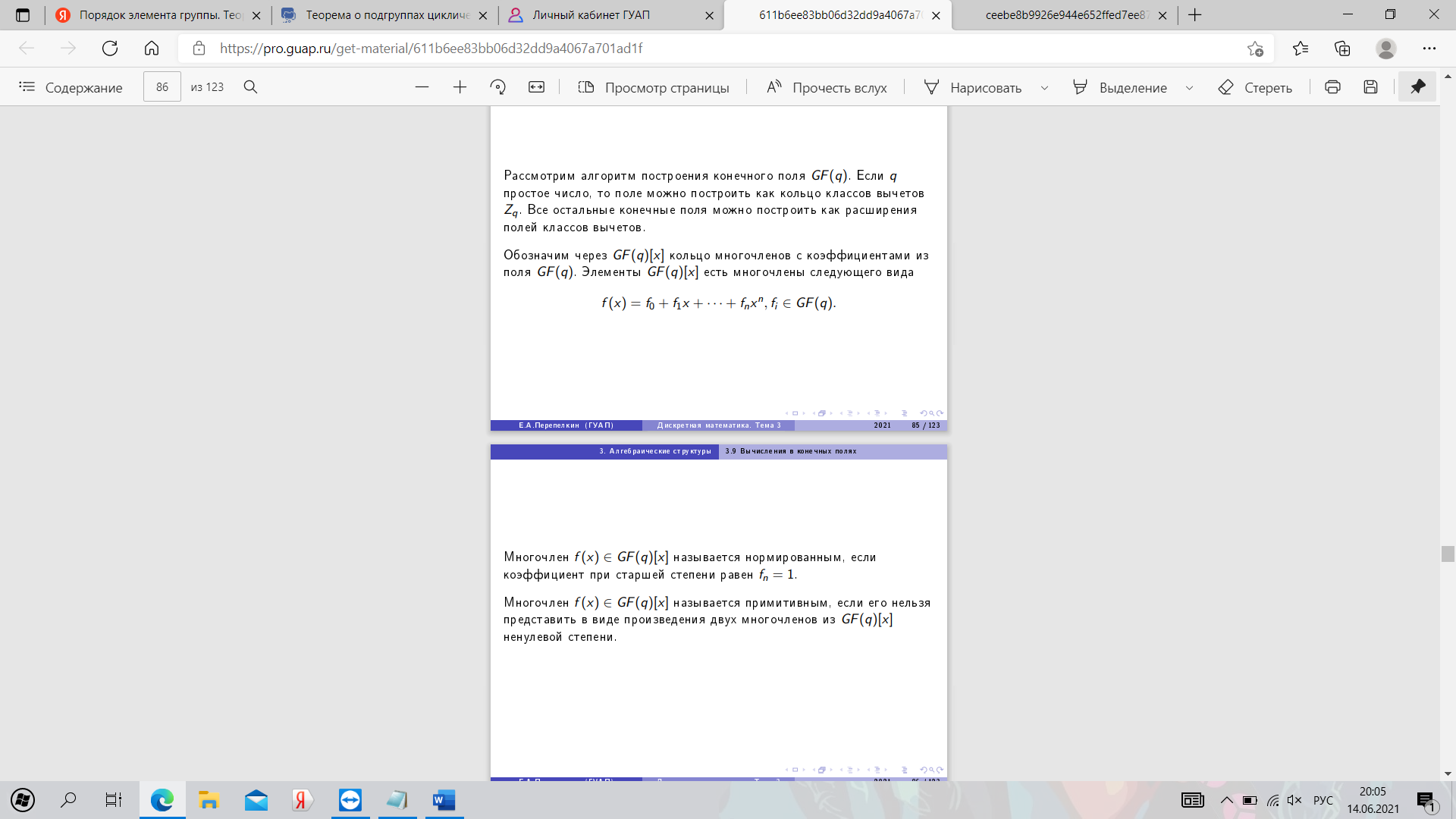
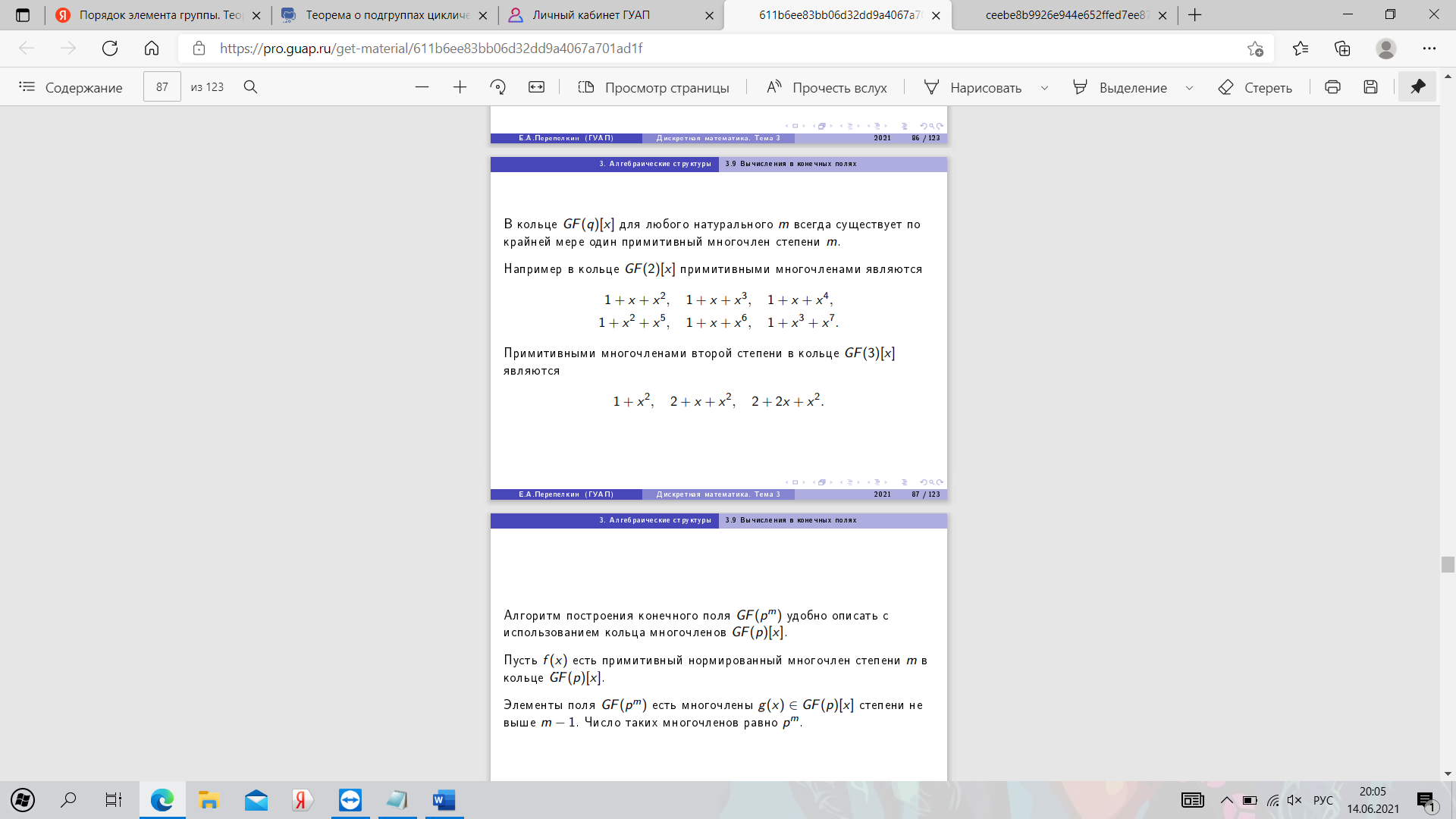
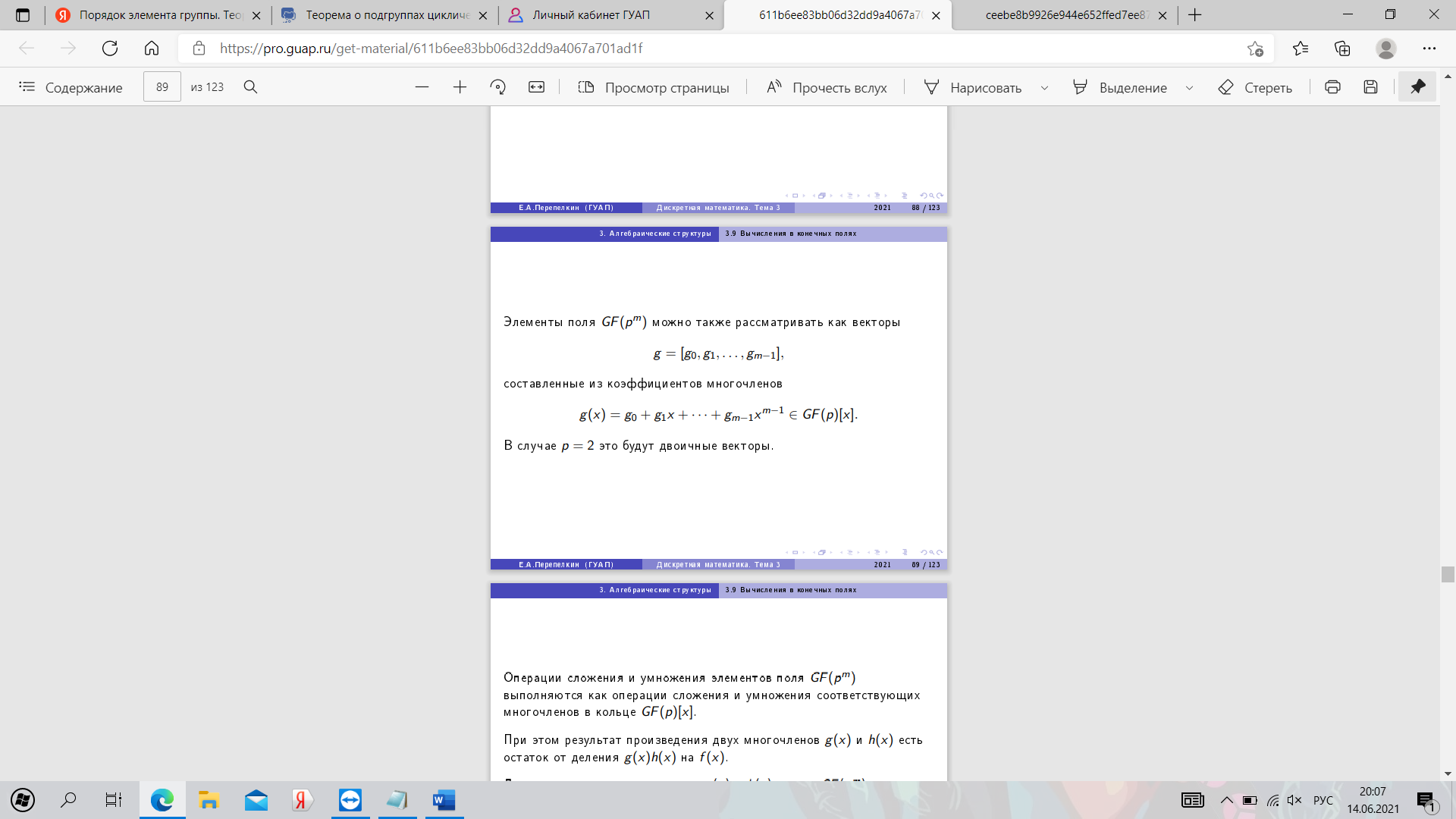
25. Алгоритм построения конечного поля

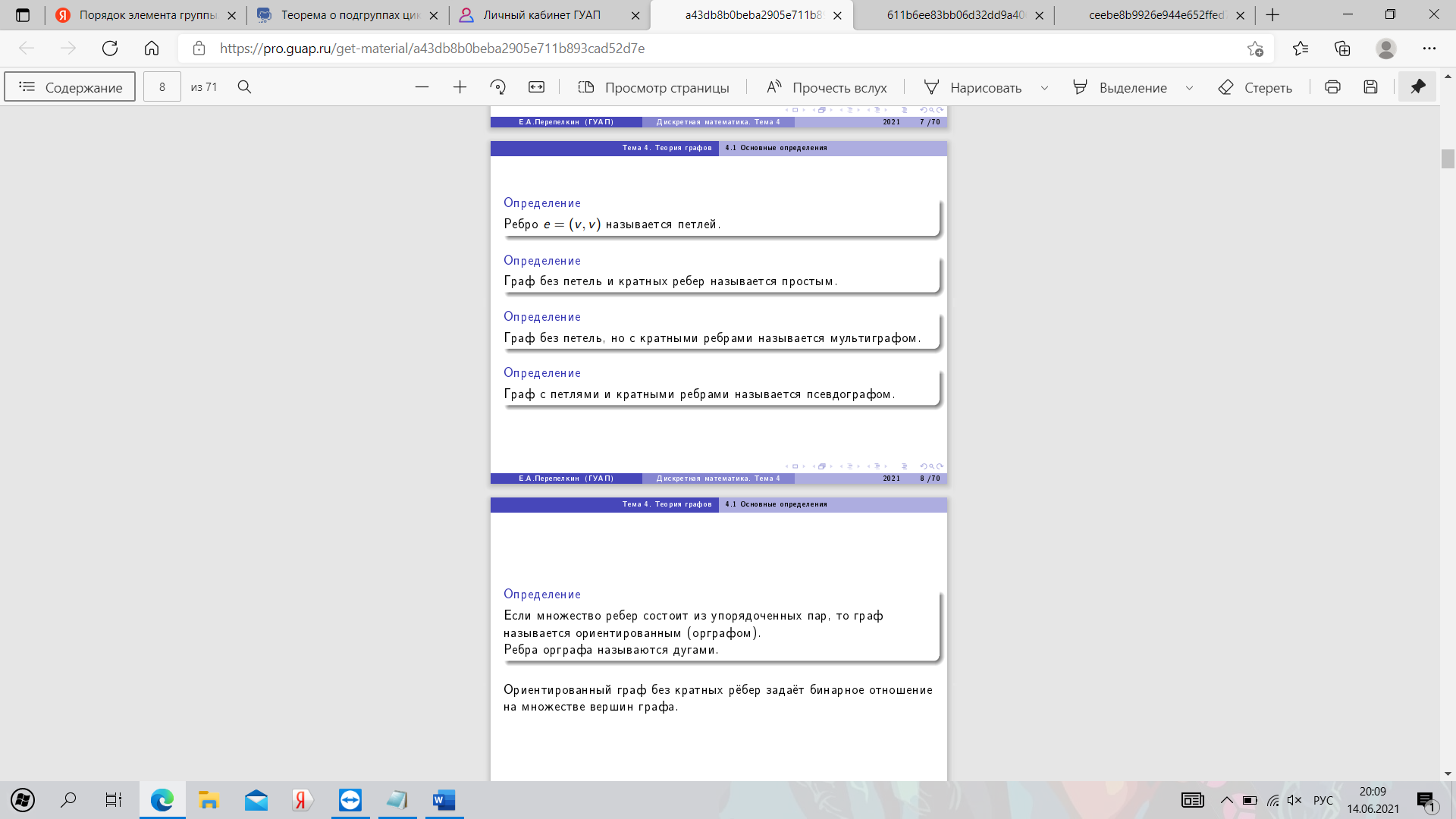
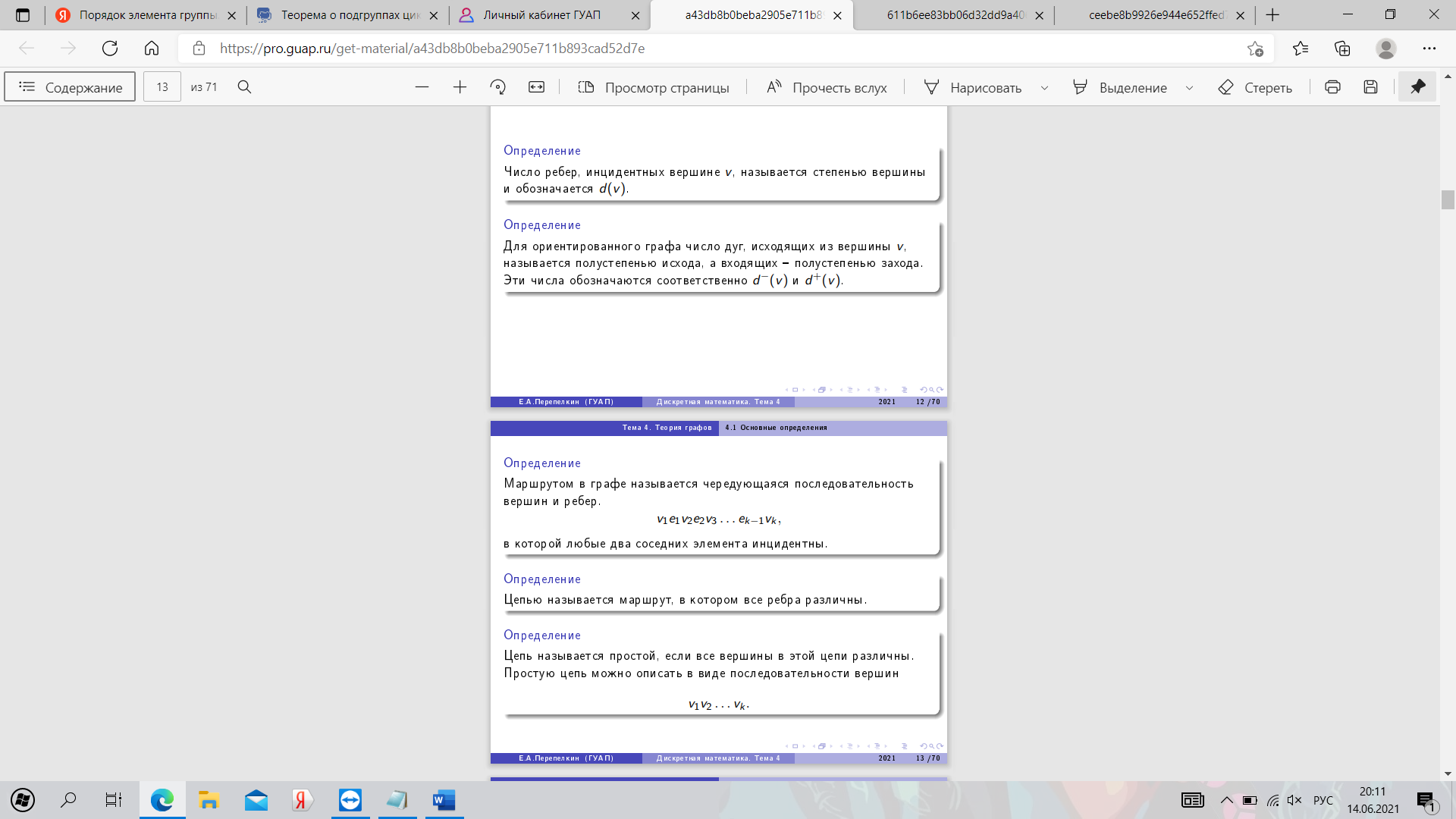
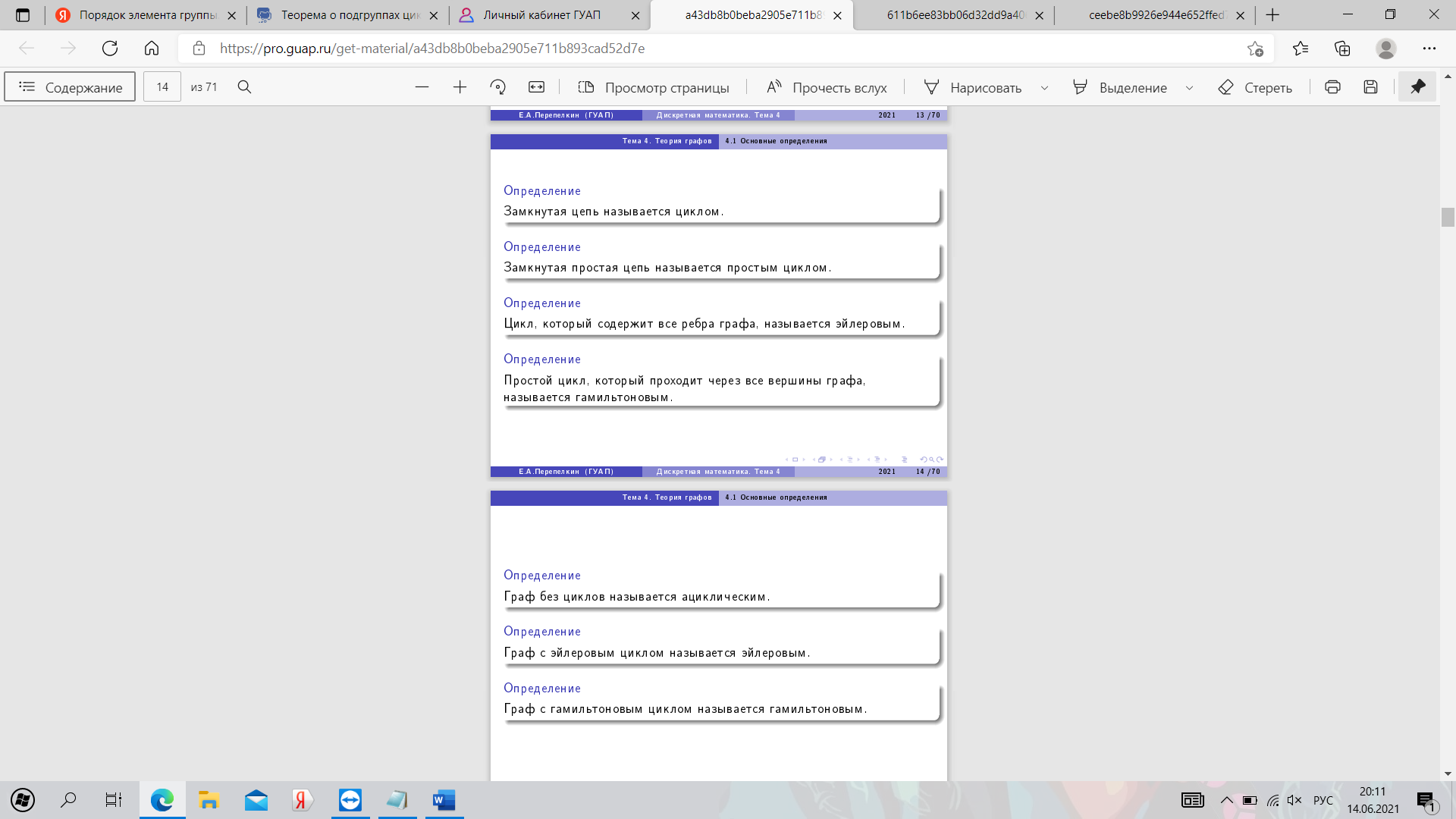
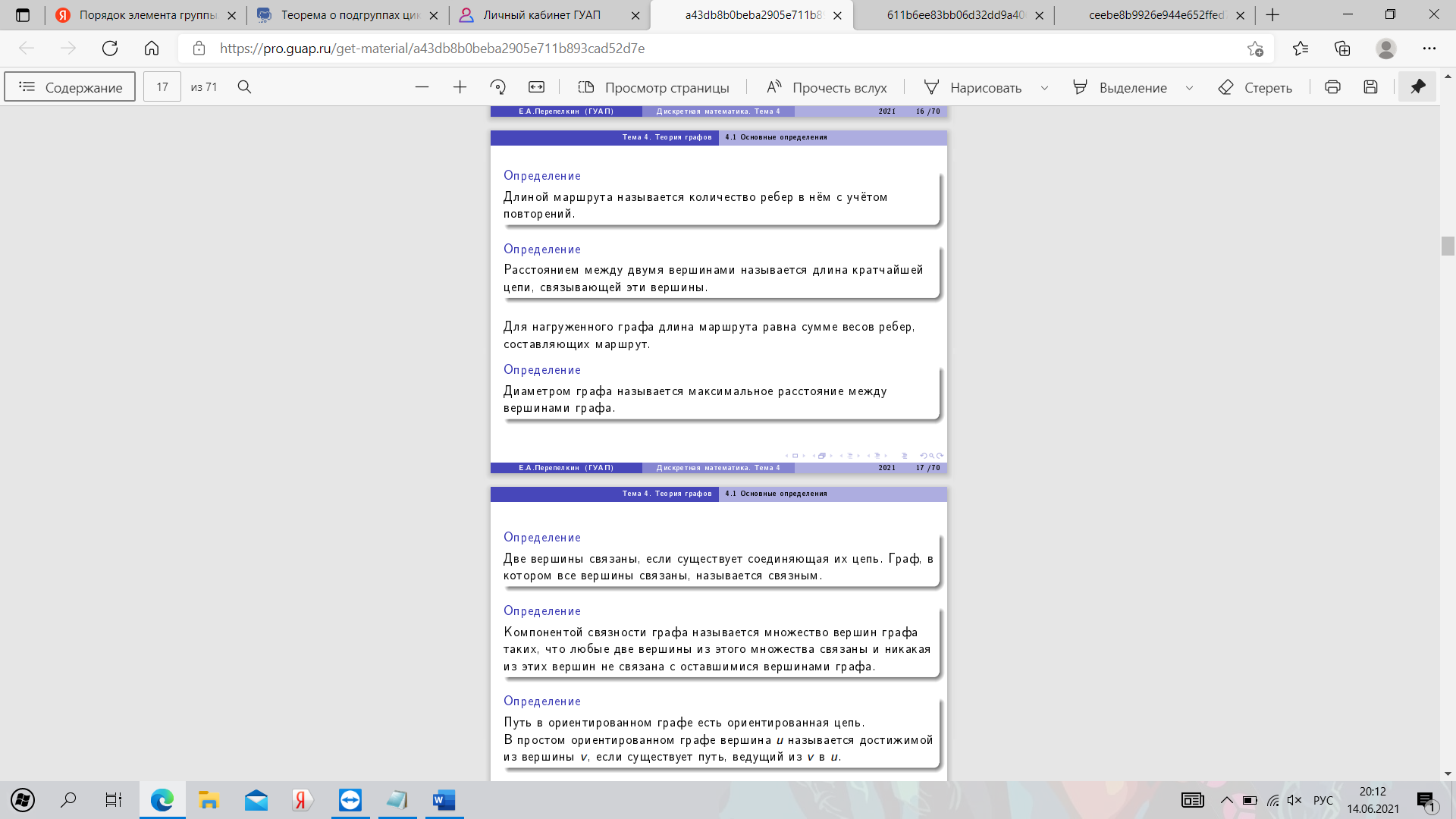
26. Основные понятия теории графов. Маршруты в графах.

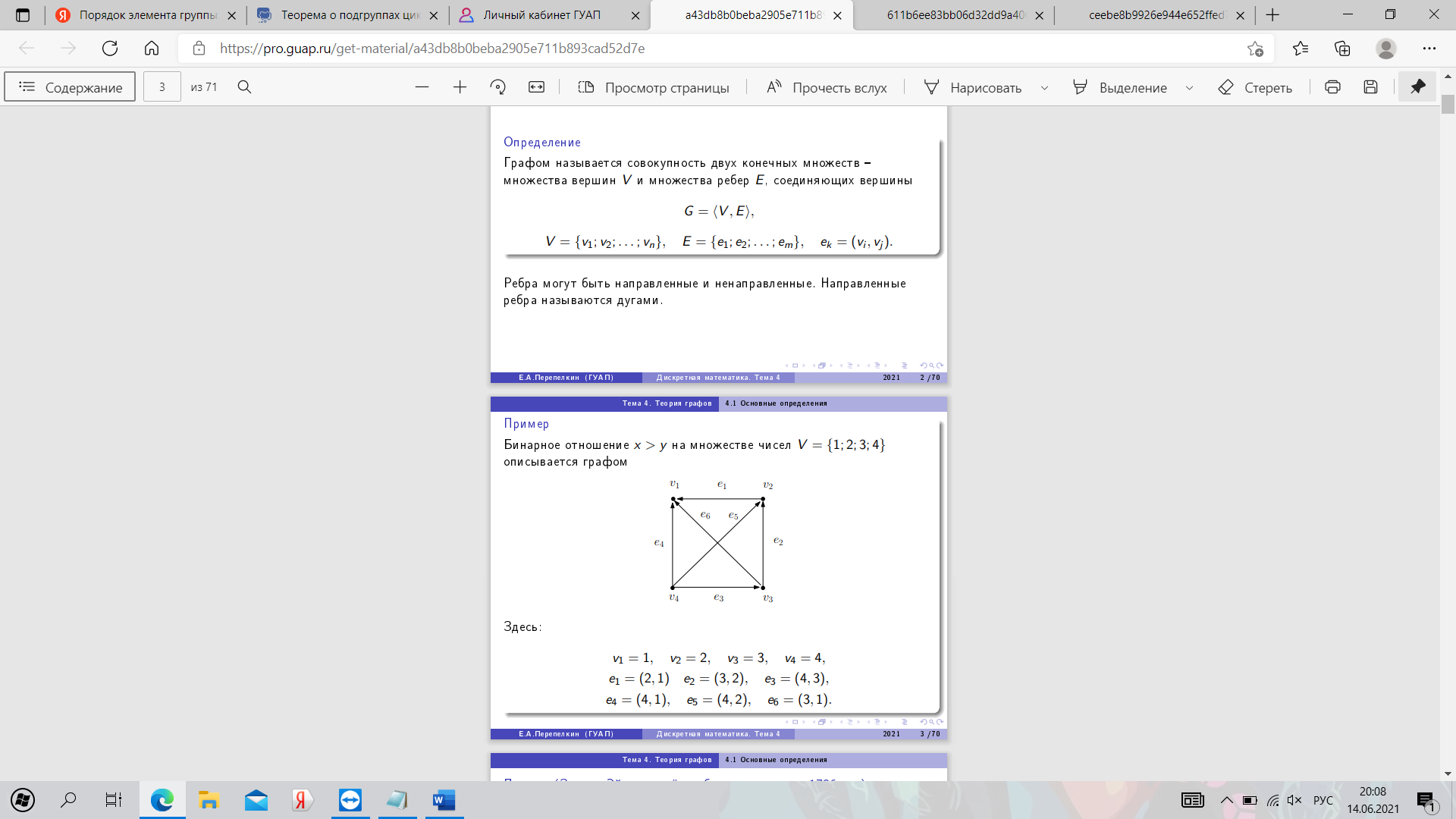
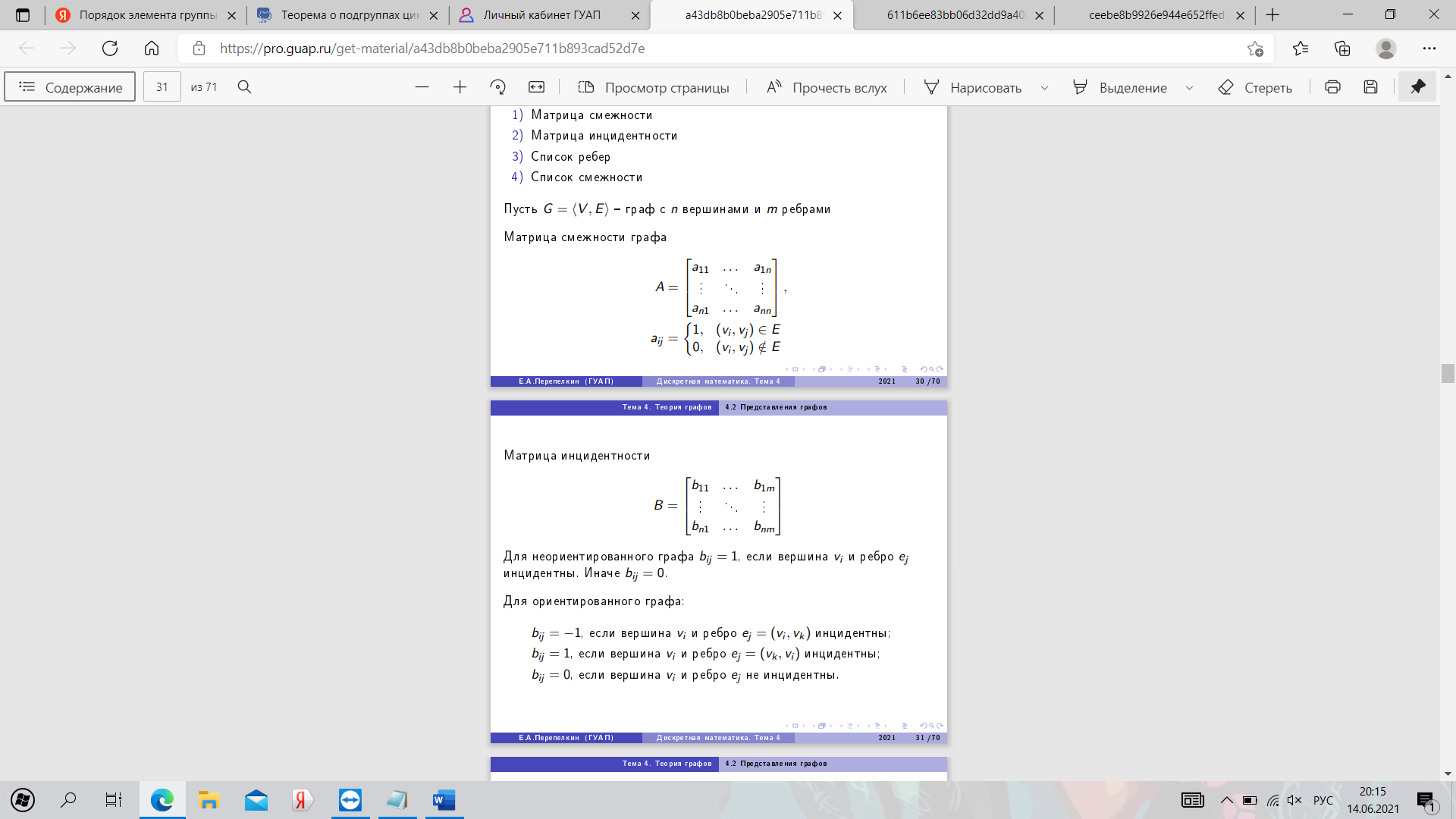
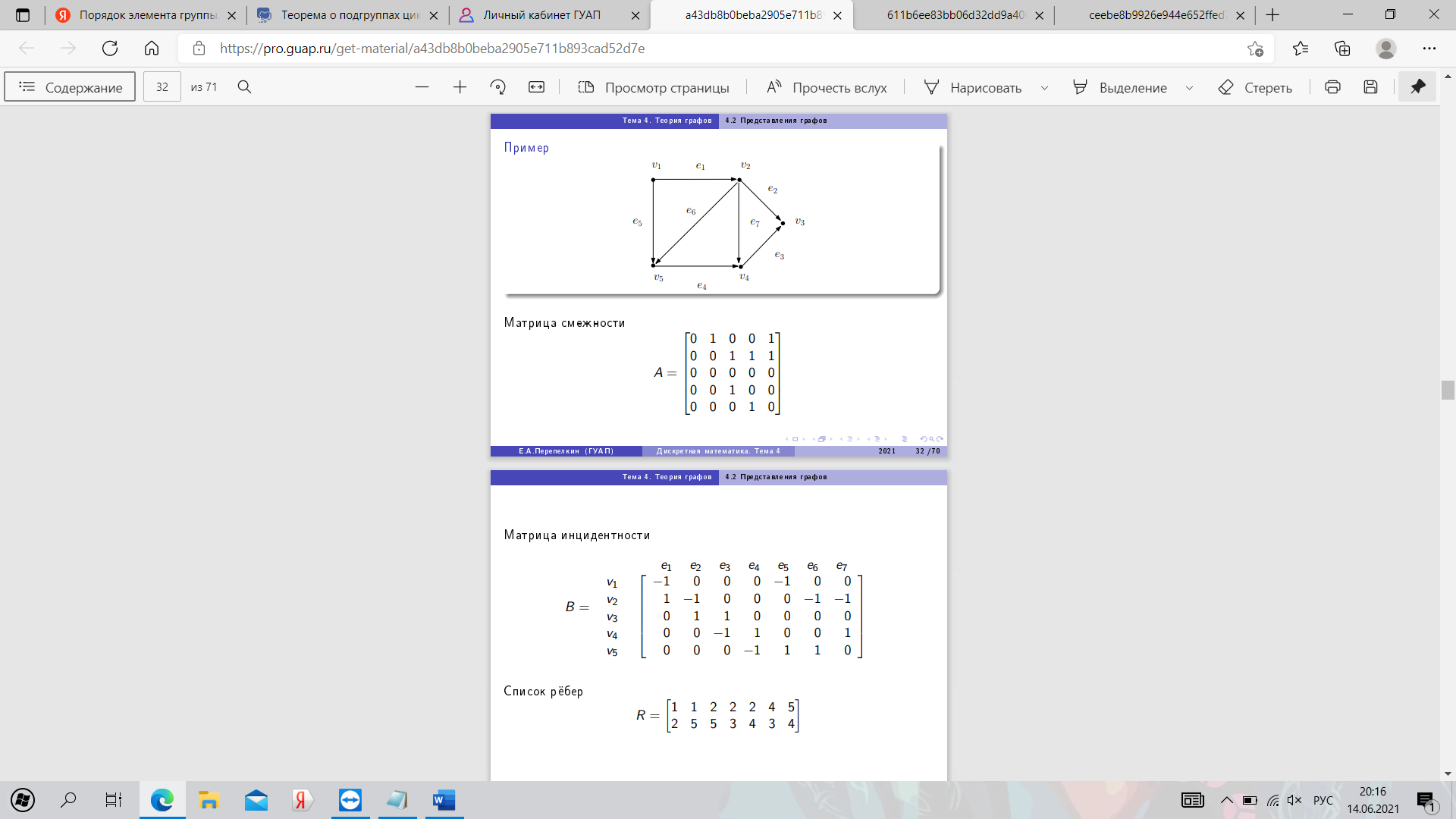
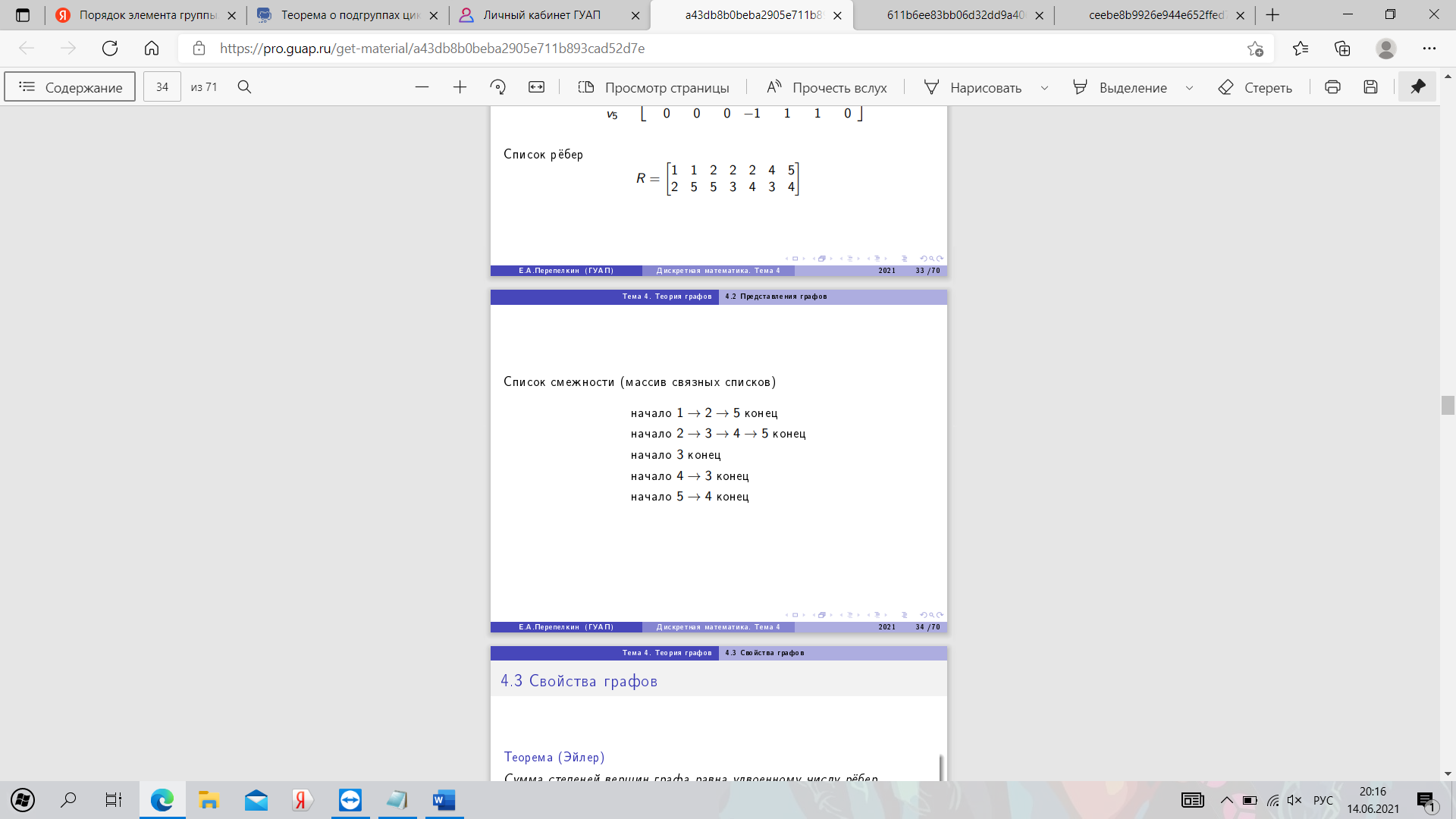
27. Представления графов. Пример.

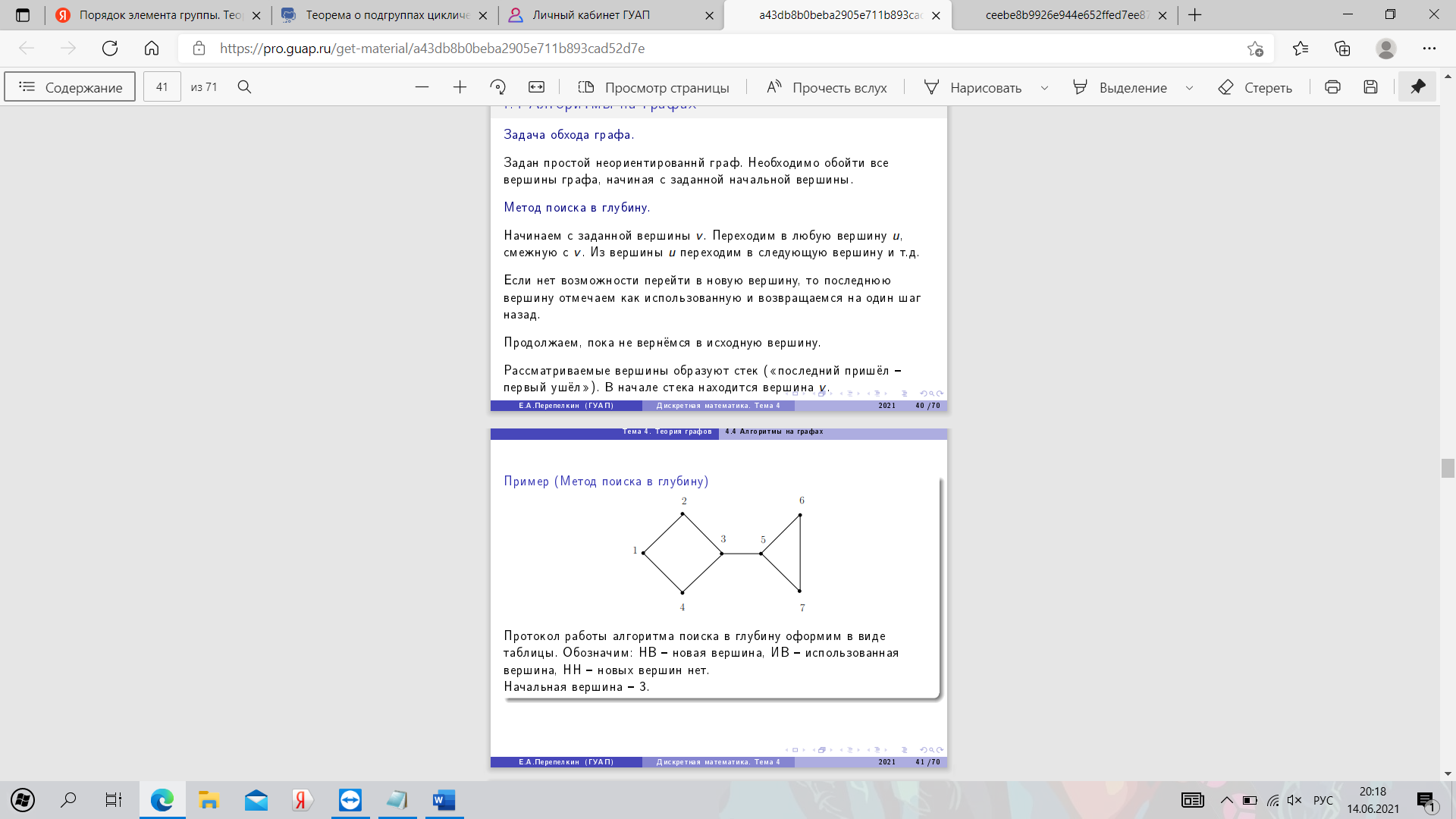
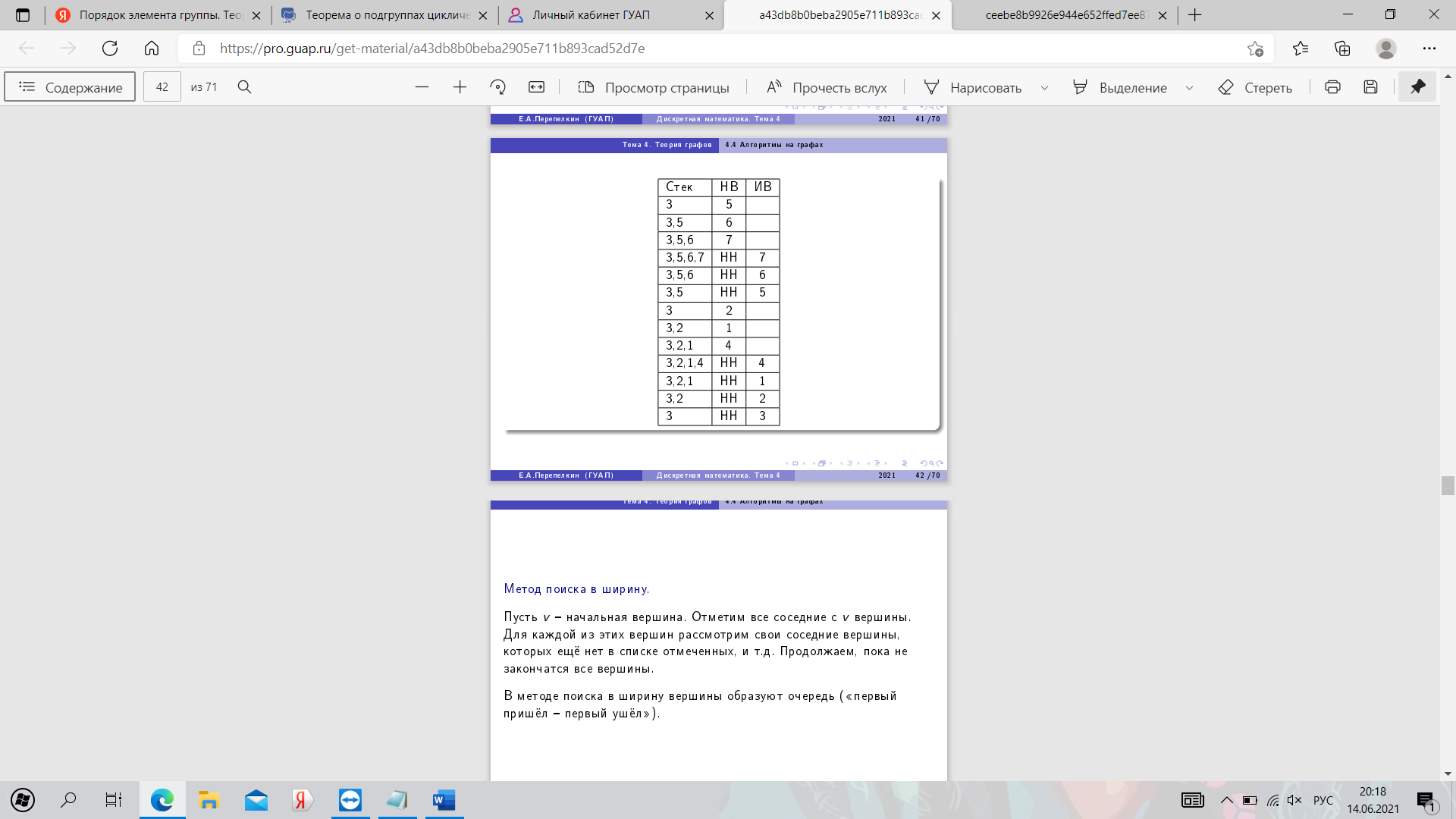
28. Алгоритмы обхода графа в ширину и глубину. Пример.

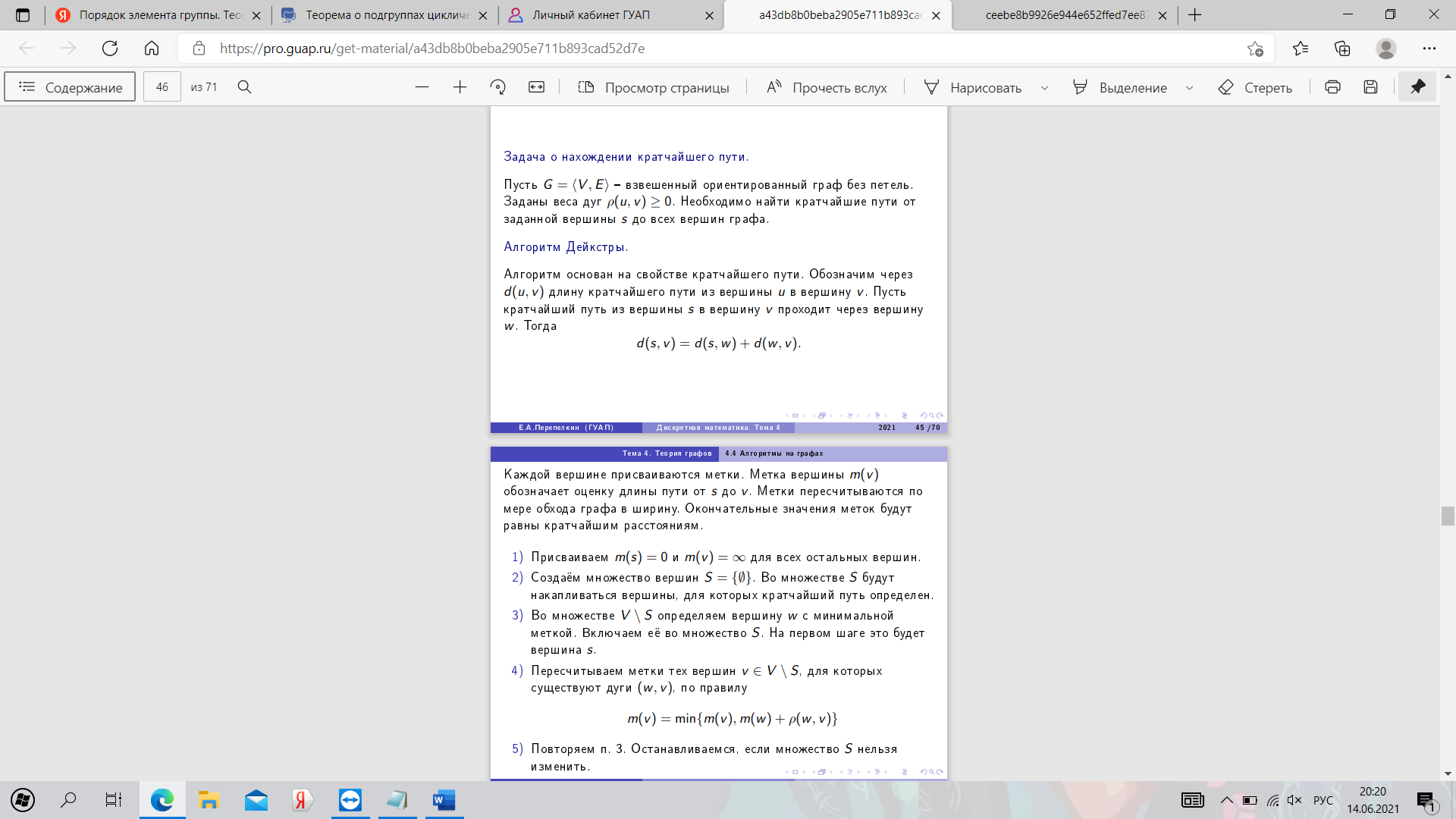
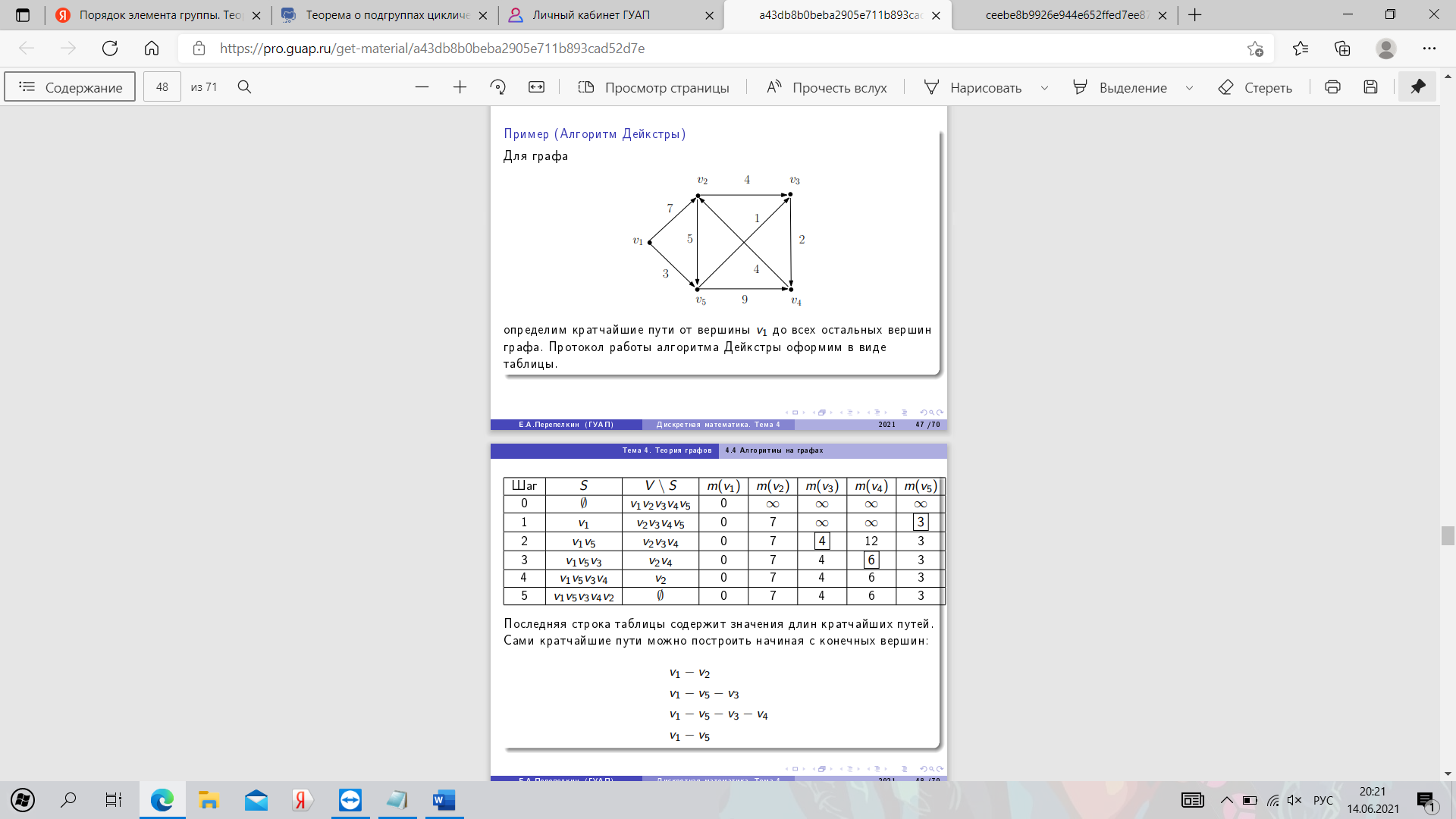
29. Алгоритм Дейкстры. Пример

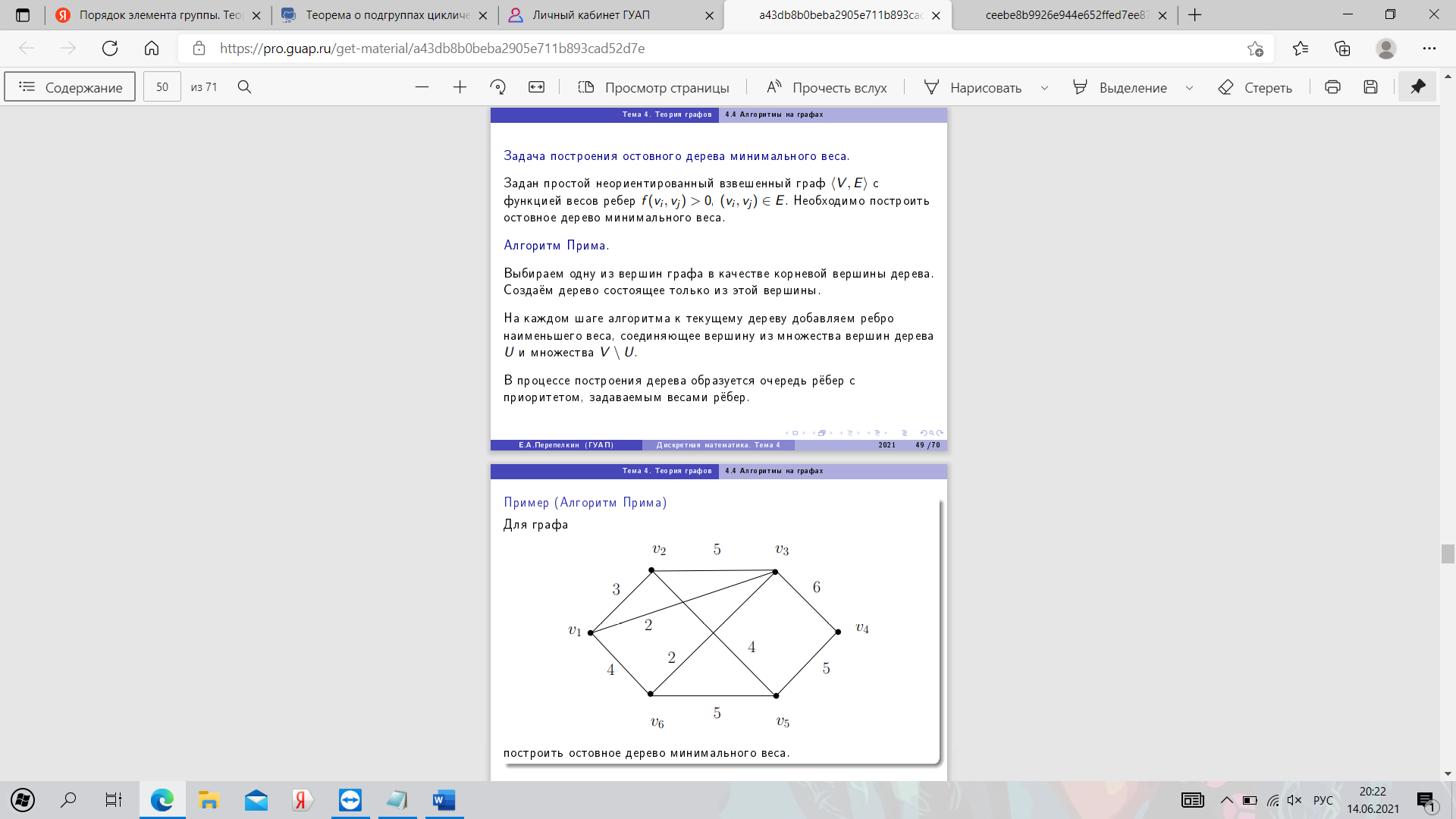
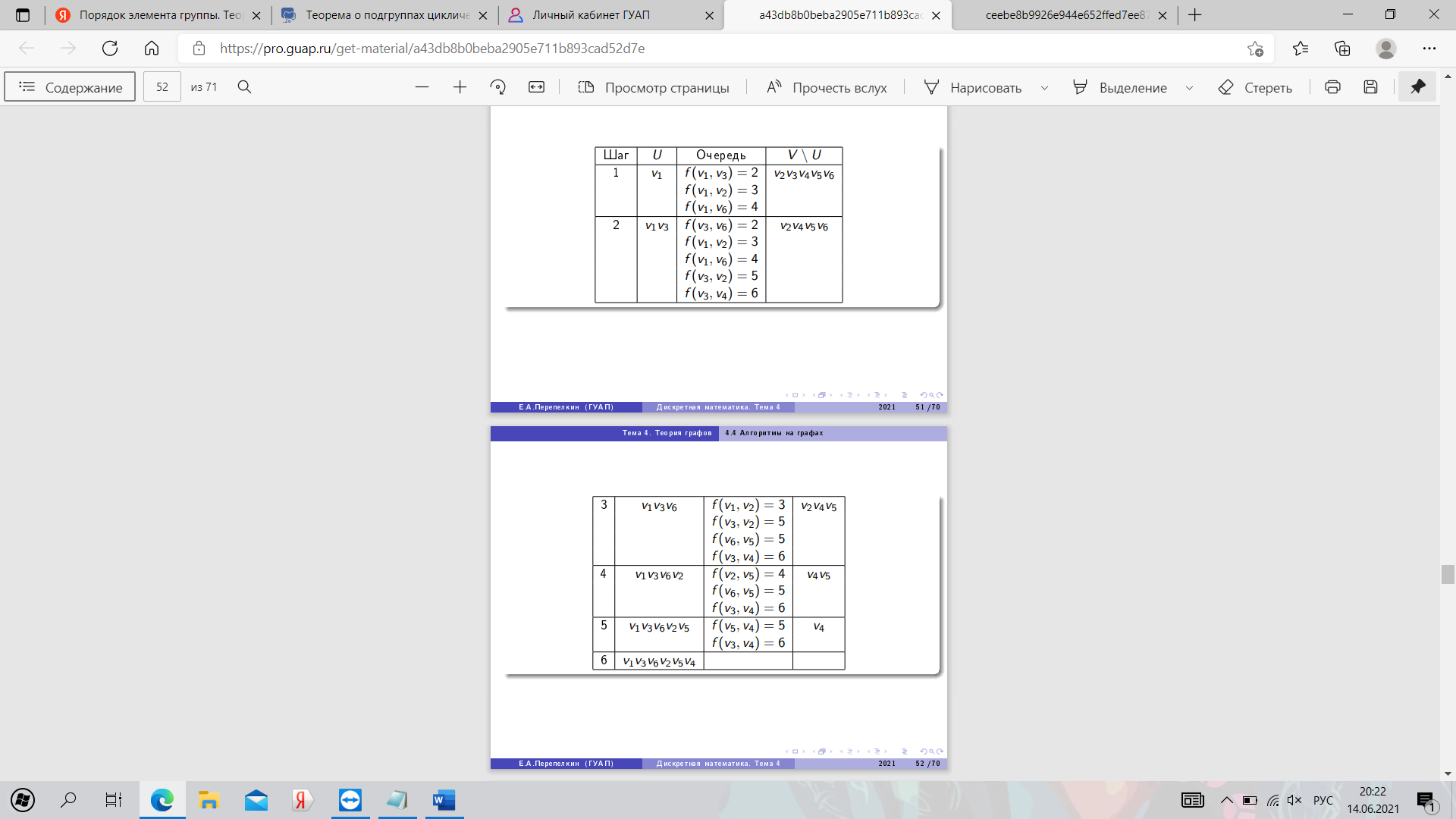
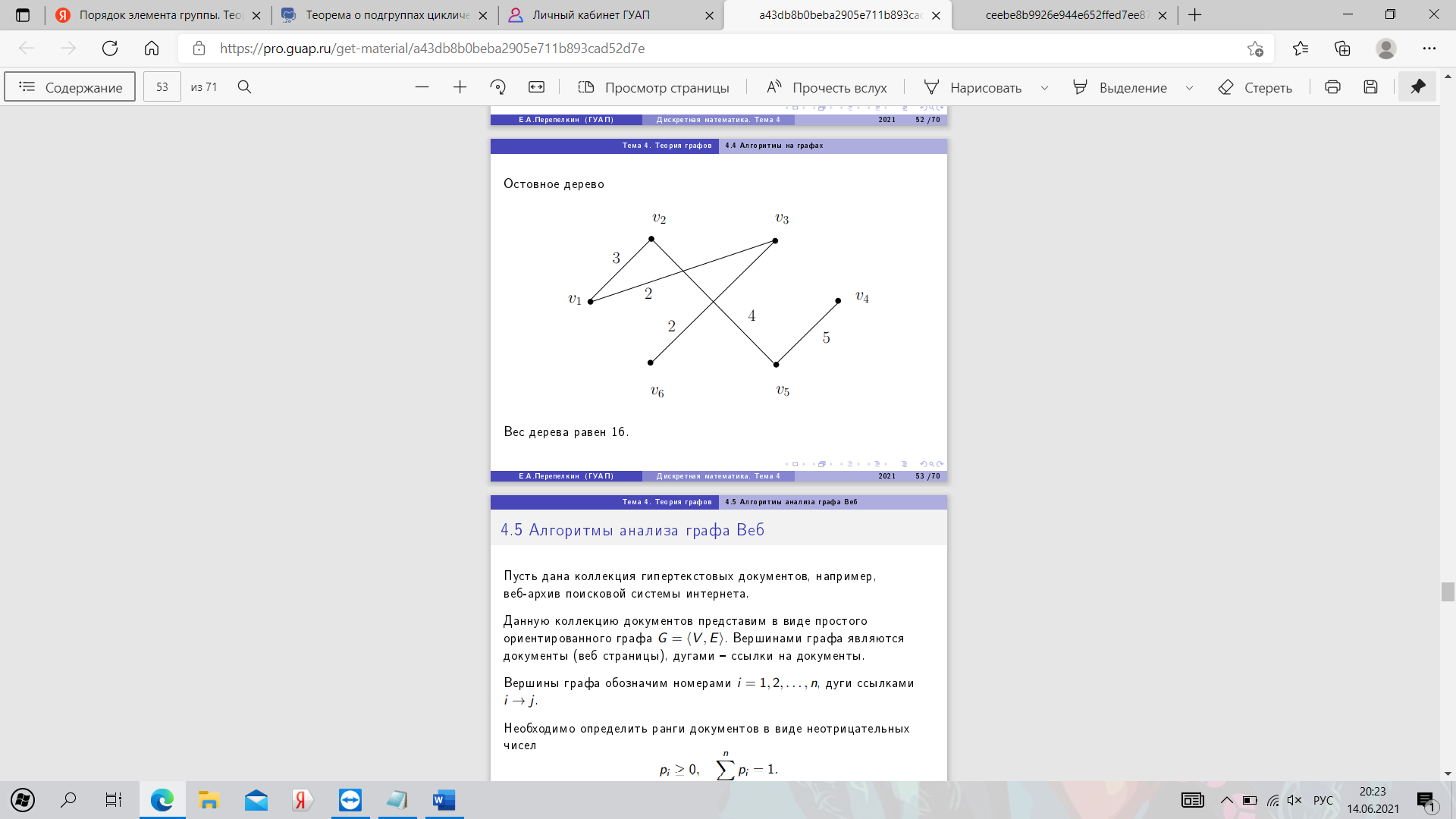
30. Алгоритм Прима. Пример

22