1. Характеристическая функция множества. Свойства характеристических функций

Характеристической функцией множества A называется функция принадлежности элементов U множеству А

Множества совпадают тогда и только тогда, когда совпадают их характеристические функции

Свойства характеристических множеств:

1

2.

3.

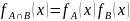
4.

5.

6.

2. Теоретико-множественные тождества. Методы доказательства тождеств. Пример.

1. Коммутативность

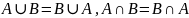
2. Ассоциативность

3. Дистрибутивность

4. Законы де Моргана

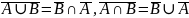
5. Идемпотентность

6. Поглощение

7. Свойства нуля A ∪ ∅ = A, A ∩ ∅ = ∅.

8. Свойства единицы

9. Инволютивность

10. Свойства дополнения

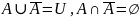
Доказать теоретико-множественные тождества можно методом включения и методом характеристических функций

Метод включения заключается в том, что A и B равны, если

Значит, ∀x : x ∈ A ⇒ x ∈ B и x ∈ B ⇒ x ∈ A, или ∀x : x ∈ A ⇔ x ∈ B.

Для доказательства равенства множеств A и B методом характеристических функций достаточно доказать, что ∀x : f_А(x) = f_В(x)

3. Формула включения исключения

Пусть А₁, …, А_n есть подмножества некоторого конечного множества А. Тогда

Докажем на основе принципа математической индукции. Базис индукции. При n=2 получим

Шаг индукции. Пусть теорема справедлива для (n-1)-го подмножества. Тогда

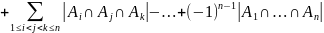
4. Декартово произведение множеств. Свойства декартова произведения.

Прямым(декартовым) произведением множеств

Называется множество всех упорядоченных наборов

Свойства произведения:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

5. Композиция бинарных отношений. Свойства операций над бинарными отношениями.

Композицией бинарных отношений называется отношение

Свойства операций над бинарными отношениями:

1. 

2. 

3. 

4. 

5. 

6. (

7. 

6. Свойства бинарных отношений: рефлексивность, симметричность, транзитивность, плотность.

Отношение называется рефлексивным, если

Отношение называется антирефлексивным, если не существует что xRx

Отношение называется симметричным, если

Отношение называется антисимметричным, если не существует таких, что одновременно xRy и yRx

Отношение называется транзитивным, если для

Отношение называется плотным, если zRy

7. Отношение эквивалентности. Классы эквивалентности. Теоремы о разбиении множества на классы эквивалентности.

Отношение называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно

Пусть . Множество называется классом эквивалентности

Теорема

Классы эквивалентности образую разбиение множества А

Доказательство

Теорема

Любое разбиение множества А порождает отношение эквивалентности на этом множестве

Доказательство

Пусть

Определим отношение

Выполняются все три свойства: рефлексивность, симметричность, транзитивность