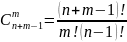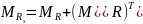8. Замыкания бинарных отношений. Теорема о замыканиях.

Отношение называется замыканием отношения относительно свойства p, если:

1. 

2. 

3. является подмножеством любого другого отношения, включающего в себя R и обладающего свойством p

Теорема о замыканиях

1. Рефлексивное замыкание

2. Симметричное замыкание

3. Транзитивное замыкание

9. Матрицы бинарных отношений и их свойства

Пусть – бинарное отношение на конечных множествах

Матрица M_R отношения R состоит из столбцов

Элементы M_R принимают два значения: 0, 1. Такого рода матрицы называются логическими или булевыми.

Свойства бинарных отношений:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

10. Отношение порядка. Упорядоченные множества. Диаграмма Хассе.

Антисимметричное транзитивное отношение называется отношением порядка. Обозначается . Если , то говорят, что x предшествует у.

Рефлексивное отношение порядка называется отношением нестрогого порядка. Обозначается

Антирефлексивное отношение порядка называется отношением строгого порядка. Обозначается

Отношение порядка называется отношением полного порядка, если для любых x, y или . Иначе отношение порядка называется отношением частичного порядка.

Множество А с заданным на нём отношением порядка называется упорядоченным и обозначается

Упорядоченное множество с полным порядком называется вполне упорядоченным, если в любом его непустом подмножестве есть минимальный элемент.

Конечное упорядоченное множество можно представить в виде диаграммы Хассе. В ней элементы множества изображаются в виде точек на плоскости. Точки х и у соединяются линией, если

Диаграмма Хассе выглядит так:

11. Перестановки, размещения, сочетания. Вывод формул для основных комбинаторных чисел.

Перестановкой n элементов называется упорядоченная (n,n)-выборка без повторений.

Размещением из n элементов по m называется упорядоченная (n,m)-выборка

Сочетанием из n элементов по m называется неупорядоченная (n,m)-выборка

Обозначим:

Справедливы формулы:

Доказательство:

При построении размещений без повторений первый элемент размещения можем выбрать n способами, второй n-1 способами, последний n-m+1 способами. Выбор осуществляется последовательно. Таким образом, по правилу произведения

Перестановки – это размещения без повторений в случае m=n. Поэтому

Сочетания без повторений – это неупорядоченные (n,m)-выборки. Из каждого сочетания можно получать m! размещений с помощью перестановки элементов сочетания.

Поэтому справедливо отношение

При построении размещений с повторениями первый элемент размещения можем выбрать n способами, второй и последующие также n способами. Поэтому по правилу произведения

Рассмотрим сочетания с повторениями. Пусть

Каждая неупорядоченная выборка с повторениями может быть записана в следующем виде , где

Выборку можно закодировать булевым вектором

, где 0 выполняет роль разделителя

Таким образом, число выборок равно числу булевых векторов длины n+m-1, содержащих ровно m единиц, и равно