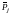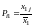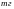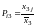Оцінки якості ґрунтів
Номер госпо-дарства |
Вміст гумосу |
Вміст фосфору |
Кислотність |
|
|
||||||
% |
|
|
|
|
|
||||||
|
|
|
|||||||||
1 |
3.1 |
0.92 |
19.8 |
0.91 |
6.5 |
1.03 |
2.86 |
0.95 |
|||
2 |
4.0 |
1.18 |
25.5 |
1.16 |
6.5 |
1.03 |
3.37 |
1.12 |
|||
3 |
2.4 |
0.71 |
18.2 |
0.83 |
5.8 |
0.91 |
2.45 |
0.82 |
|||
4 |
3.7 |
1.10 |
22.8 |
1.04 |
6.3 |
0.99 |
3.13 |
1.04 |
|||
5 |
2.3 |
0.68 |
19.8 |
0.91 |
6.1 |
0.96 |
2.55 |
0.85 |
|||
6 |
3.9 |
1.15 |
20.6 |
0.94 |
6.2 |
0.98 |
3.07 |
1.02 |
|||
7 |
2.9 |
0.86 |
21.9 |
1.00 |
6.2 |
0.98 |
2.84 |
0.95 |
|||
8 |
4.0 |
1.18 |
23.4 |
1.07 |
6.5 |
1.03 |
3.28 |
1.09 |
|||
9 |
3.9 |
1.15 |
25.3 |
1.16 |
7.0 |
1.10 |
3.41 |
1.14 |
|||
10 |
3.6 |
1.07 |
21.4 |
0.98 |
6.3 |
0.99 |
3.04 |
1.02 |
|||
Sum |
33.8 |
10.00 |
218.7 |
10.00 |
63.4 |
10.00 |
30.00 |
10.00 |
|||
Average |
3.38 |
- |
21.87 |
- |
6.34 |
- |
- |
- |
|||
Poзpaxoвaнi бaгaтoвимipнi cepeднi дають змогу здійснити пopiвняльнy оцінку якості ґрунтів по гpyпi гocпoдapcтв за тpьoмa найважливішими їхніми ознаками. З даних таблиці видно, що кращі ґрунти мають дев'яте і друге господарства, а гірші - третє і п'яте господарства.
Середню багатовимірну використовують для аналізу господарської діяльності підприємств, зокрема при визначенні ефективності використання виробничого потенціалу (землі, трудових ресурсів, виробничих фондів) та ін.
Приклад 4.
У окремих випадках виникає потреба визначити узагальнений середній показник по декількох ознаках одночасно. Він також має назву багатомірної середньої. При цьому осереднюються не абсолютні значення ознак, а коефіцієнти відношення до середнього рівня для кожної ознаки. Названі коефіцієнти визначаються за приведеними нижче формулами. Приклад розрахунку багатомірної середньої :
Таблиця 5.