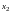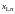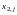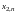Лабораторна робота №3 Метод багатовимірної середньої

У практичній діяльності досить часто доводиться стикатися з проблемою раціонального вибору (найкращого з точки зору суб'єкта, що приймає рішення) одного або декількох об'єктів з множини аналогічних. При цьому, як правило, об'єктивна (числова) оцінка, що має статистичний характер, базується на низці спостережень про характер поведінки досліджуваної множини цих об'єктів. Якщо кожен з елементів такої множини характеризується однією числовою характеристикою, то проблема вибору очевидна – якщо, звичайно, особа, яка приймає рішення, знає, що хоче. Досить розташувати елементи в порядку зростання характеристики, що відбиває його привабливість (наприклад, товари однакової ціни, але з різними споживчими якостями).

Однак, якщо в розрахунок приймається не одна, а дві, три або більше характеристик порівнюваних об'єктів, проблема стає значно складнішою. Пряме порівняння тут неможливе, бо у різних об'єктів є сильні і слабкі сторони. Як правило, якщо перший з однотипних об'єктів перевершує другий за однією характеристикою, то поступається йому за іншою.

Завдання ще більше ускладнюється, якщо об'єкти характеризуються показниками, виміряними в різних одиницях. Звичайно, в деяких випадках можна довіритися інтуїтивним рішенням, заснованим на емоційних мотивах. Так, зазвичай, і відбувається в повсякденному житті. Але ситуація змінюється, коли мова заходить про принципові рішення: вибір банку для відкриття рахунку фірми, покупка дорогого промислового устаткування, вибір сегмента ринку для розвитку бізнесу. В рішенні таких задач бажано щоб емоційні мотиви знайшли опору в об'єктивній числовій оцінці. Іншими словами, потрібно певний апарат, що дозволяє порівнювати об'єкти, які характеризуються цілим набором ознак, тобто багатовимірні об'єкти, з урахуванням всіх цих ознак.

Особливим видом середніх величин є середня багатовимірна, яка являє собою середню величину кількох ознак для однієї одиниці сукупності. Оскільки неможливо розрахувати середню величину за абсолютними значеннями різних ознак (різноякісних, виражених у різних одиницях виміру), то багатовимірна середня визначається з відносних величин (часток, процентів і т.п.), як правило, з відношень абсолютних значень для одиниці сукупності до середніх значень цих ознак.

Це найбільш простий з розглянутих тут і тим не менш дуже дієвий метод обробки результатів спостережень над багатовимірними величинами. Багатовимірна середня характеризує елемент сукупності за набором ознак, а звичайна середня характеризує сукупність елементів за однією ознакою.

Визначення рангів обʼєктів

Вихідними даними в задачах багатовимірного аналізу є набір векторів 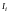, , обраних в якості множини об'єктів, що підлягають ранжуванню. Як правило, це досить однорідний масив. Він складається з різних векторів (об'єктів) однакової розмірності (кожен об'єкт є охарактеризований заданим набором різних ознак):

, , … .

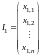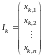Таким чином, є характеристикою -го об'єкта за -ою ознакою.

Нехай, потрібно провести ранжування об'єктів, які охарактеризовані деяким числом різнорідних ознак.

Для реалізації алгоритму зручно формалізувати вихідні дані у вигляді таблиці (табл. 1):

Таблиця 1.

		Вихідні дані
Обʼєкти	Характеристики ознак

Кожен з рядків цієї таблиці містить інформацію про один з об'єктів за усіма ознаками (різнорідні дані з різними одиницями виміру), а кожен стовпець – інформацію про кожен об'єкт за однією ознакою (однорідні дані з однаковою одиницею вимірювання).

Середнє арифметичне, обчислене по кожному із стовпців , де 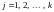, дає середнє значення ознаки для усієї групи обʼєктів:

.

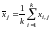Для приведення даних к до вигляду, що допускає порівняння, необхідно здійснити їх нормування, для чого дані кожного стовпчика поділити на відповідне середнє за ознакою:

.

Результатом такого нормування є безрозмірні значення 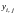, що характеризують ознаки об'єктів. Якщо всі розглянуті об'єкти є досить однорідними, то отримані в результаті нормування величини будуть не тільки позбавлені розмірності, але і будуть являти собою набір чисел, близьких до одиниці.

Дійсно, величина показує, у скільки разів -й показник, обчислений для -го об'єкта, перевершує відповідне середнє значення цієї ознаки для усієї множини аналізованих об'єктів.

Після цієї процедури кожен об'єкт може бути охарактеризований за всіма нормованим ознаками середнім значенням – , тобто одним числом. Тепер можливе ранжування за принципом «чим більше, тим краще» – або, навпаки, в залежності від напрямку показників.

Таблиця 2.