
РГР_2023_3 семестр
.pdf
МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. Р.Е.АЛЕКСЕЕВА
Институт радиоэлектроники и информационных технологий Кафедра «Электроника и сети ЭВМ»
Расчетно-графическая работа
по дисциплине «Электротехника и электроника»
Вариант 00
РУКОВОДИТЕЛЬ: |
|
|
________________ |
Калинина Н.А. |
|
(подпись) |
(фамилия, и.,о.) |
|
СТУДЕНТ: |
|
|
________________ |
|
|
|
|
|
(подпись) |
(фамилия, и.,о.) |
|
|
|
|
|
(шифр группы) |
|
Работа защищена «___» ____________
С оценкой ________________________
Нижний Новгород
2023
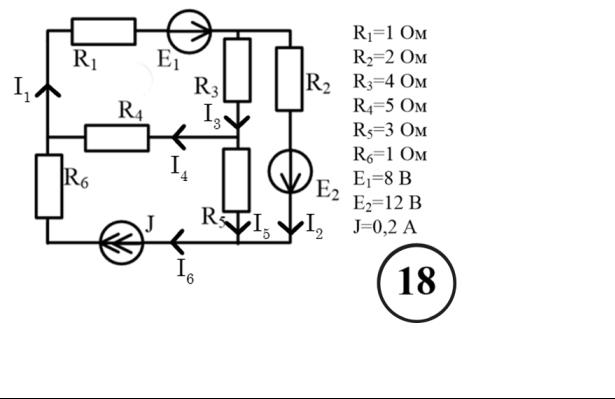
Задание:
Ответы:
Метод решения |
|
|
|
|
|
|
|
Метод контурных |
|||||||
Законы Кирхгофа |
1,776 |
2,189 |
-0,414 |
1,576 |
-1,989 |
0,2 |
|
|
|||||||
токов |
1,776 |
2,189 |
-0,414 |
1,576 |
-1,989 |
0,2 |
|
|
|
|
|
|
|
||
Метод узловых |
1,775 |
2,1885 |
-0,413 |
1,575 |
-1,99 |
0,2 |
|
потенциалов |
|||||||
|
|
|
|
|
|
||
Метод наложения |
|
|
|
|
|
|
|
Метод эквивалентного |
1,75 |
|
|
|
|
|
|
генератора |
|
|
|
|
|
||
|
|
|
|
|
|
2
Задача 1. Найти токи во всех ветвях с применением законов Кирхгофа.
Дано:
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1. |
Определить количество узлов и ветвей в схеме, расставить токи, обозначить узлы. |
|||||||||||||||||
|
|
Количество узлов: 4 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Количество ветвей: 6 |
|
|
|
|
|
|
|
|
|
|
||||||
2. |
Определить количество уравнений по первому и второму законам Кирхгофа, |
|||||||||||||||||
|
выбрать направления обхода контуров. |
|
|
|
|
|
|
|||||||||||
|
|
Количество уравнение по первому закону Кирхгофа: |
|
|||||||||||||||
|
|
n1=Ny−1=3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Количество уравнение по второму закону Кирхгофа: |
|
|||||||||||||||
|
|
n2=Nв−(Ny−1)=6−(4−1)=3 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
Направления обхода контуров указаны на чертеже. |
|
|||||||||||||||
3. |
|
|
I1 |
− I3 |
− I2 |
= 0 |
|
|
|
|
|
|
|
|
|
|
||
|
I3 |
− I4 |
−I5 |
= 0 |
|
|
|
|
|
|
|
|
|
|
||||
Записать систему уравнений. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
I1R1 |
I2 |
+ I5 |
−I6 |
= 0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
+ I3R3 |
+ I4R4 |
= E1 |
|
|
|
|
|
|
|
|
|
|
||||
|
I2R2 |
− I5R5 |
−I3R3 |
= E2 |
|
|
|
|
|
|
|
|
|
|
||||
4. |
|
|
I6 = J = 0,2 A |
|
|
|
|
|
|
|
|
|
|
|
||||
Проверить соответствует ли число уравнений системы числу неизвестных. |
||||||||||||||||||
|
|
Количество неизвестных: 5 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
Количество уравнений системы: 5 |
|
|
|
|
|
|
|
|||||||||
|
|
Вывод: соответствует. |
|
|
|
|
|
|
|
|
|
|
||||||
5. |
Решить систему уравнений. |
−1 |
0 |
0 |
|
|
|
|
|
|||||||||
Решение методом Гаусса:1 |
−1 |
0 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
0 |
0 |
1 |
−1 |
−1 |
|
|
( ) |
( ) |
||
|
|
|
|
|
|
|
|
0 |
1 |
0 |
|
0 |
1 |
0,2 |
|
→ |
||
|
|
|
|
|
|
|
|
|
|
4 − |
1 = |
|||||||
|
|
|
|
|
|
|
|
1 |
0 |
4 |
|
5 |
0 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
2 |
−4 |
|
0 |
−3 |
12 |
|
|
|
|
3
1 |
|
−1 |
|
|
−1 |
|
|
0 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 |
|
0 |
|
|
1 |
|
|
|
−1 |
|
|
−1 |
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
( |
) |
|||||||||||||
0 |
|
1 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
1 |
|
|
0,2 |
|
|
→ |
|
<=> |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
2 |
= |
|||||||||||||||||||||||
0 |
|
1 |
|
|
|
5 |
|
|
|
|
5 |
|
|
|
0 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 |
|
2 |
|
|
−4 |
|
|
0 |
|
−3 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
−1 |
|
|
|
|
|
−1 |
|
|
0 |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
|
1 |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
1 |
|
|
|
|
0,2 |
|
|
|
( ) |
|
|
( ) |
|
||||||||||
|
0 0 |
|
|
|
1 −1 −1 |
|
|
|
0 |
|
|
→ |
|
|
|
|||||||||||||||||||||||||
0 |
|
|
1 |
|
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
0 |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|||||||||
|
0 |
|
|
2 |
|
|
−4 |
|
|
|
0 |
|
|
|
|
−3 |
|
12 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
−1 |
|
|
|
−1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
1 |
|
|
|
|
|
0 |
|
|
0 |
|
|
1 |
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
|
0 |
|
|
|
1 |
|
|
|
|
−1 |
|
|
−1 |
|
0 |
|
→ (4) − 5 ∙ (2) = |
|||||||||||||||||||||
0 |
|
|
0 |
|
|
|
5 |
|
|
|
|
|
5 |
|
|
|
−1 |
|
|
7,8 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
0 |
|
|
0 |
|
|
−4 |
|
|
|
|
0 |
|
|
|
−5 |
|
|
11,6 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 |
|
−1 |
|
|
|
−1 |
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 |
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
1 |
|
|
|
|
0,2 |
|
→ (5) − 4 ∙ (3) = |
||||||||||||||||
0 0 |
|
|
|
|
1 |
|
|
−1 −1 |
|
0 |
|
|
||||||||||||||||||||||||||||
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
10 |
|
|
|
|
4 |
|
7,8 |
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
2 |
|
|
|
−4 |
|
|
|
|
0 |
|
0 |
−5 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
−1 |
|
|
−1 |
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
0 |
|
|
1 |
|
|
|
|
0 |
|
|
|
0 |
|
|
1 |
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
0 |
|
|
1 |
|
|
−1 |
|
|
−1 |
|
|
|
|
0 |
|
|
→ (5) − 0,4 ∙ (3) = |
||||||||||||||||||||
0 |
|
|
0 |
|
|
0 |
|
|
|
10 |
|
|
|
4 |
|
|
7,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 |
|
|
0 |
|
1 |
0 |
|
|
−4 |
|
|
−9 |
|
11,6 |
|
|
|
|
|
0 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
−1 |
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
1 |
|
|
|
0,2 |
|
|
|
|
|
||||||||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
1 |
|
|
−1 |
|
|
|
|
−1 |
|
|
|
0 |
|
= |
|
|
||||||||||
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
10 |
|
|
|
|
|
|
4 |
|
7,8 |
|
|
|
|
||||||||||||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
−7,4 |
|
14,72 |
|
|
|
|
|
||||||||||
|
|
|
|
I1 |
− I2 |
|
− I3 |
= 0 |
|
|
|
|
|
|
|
|
|
|
I5 |
= −1,989 |
||||||||||||||||||||
|
|
|
I2 |
|
+ I3 |
|
= −0,5 |
|
|
|
|
→ |
I4 |
= 1,576 |
|
|||||||||||||||||||||||||
|
|
|
|
|
I3 |
− I4 |
|
− I5 |
= 0 |
|
|
|
|
|
|
I3 |
= −0,414 |
|||||||||||||||||||||||
|
10 ∙ I4 |
+ 4 ∙ I3 |
= −7,8 |
|
|
|
|
I2 |
= 2,189 |
|
||||||||||||||||||||||||||||||
|
|
|
−7.4 ∙ I5 |
= 14,72 |
|
|
|
|
|
|
I1 |
= 1,776 |
|
|||||||||||||||||||||||||||
6. Проверить полученное решение по первому закону Кирхгофа для узла, не использованного в−пI.13.+ I4 + I6 = 0 → −1,776 + 1,576 + 0,2 = 0
Для узла a (проверка):
7. Записать ответ (и добавить ответ наIоборот1 = 1,776титульного листа).
I2 = 2,189
I3 = −0,414
I4 = 1,576
I5 = −1,989
4
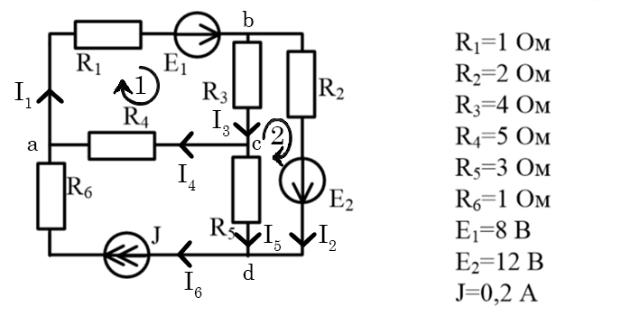
Задача 2. Найти токи во всех ветвях с помощью метода контурных токов.
Дано:
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1. |
|
Необходимость в перестройку схемы отсутствовала. Расставила направления токов |
||||||||||||||||||
|
|
|
в ветвях как в 1 задаче. |
|
|
|
|
|
|||||||||||||
|
2. |
|
Выбрала контуры-ячейки и направления контурных токов в них. |
|
|||||||||||||||||
|
3. |
|
|
|
|
|
1 |
|
= 11 |
|
|
|
|
|
|
|
|
|
|||
|
|
Запишем выражения для токов в ветвях через контурные токи. |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
3 |
= 11 |
− |
|
22 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
4 |
= 11 |
− |
|
33 |
|
|
|
|
|
|
|
|
|||||
|
|
|
5 |
= 33 |
− |
|
22 |
|
|
|
|
|
|
|
|
||||||
|
4. |
|
6 |
= 33 |
= 0,2 |
+ 4 = 1 + 4 + 5 = 10 |
11 |
= 1 |
= 8 |
|
|||||||||||
|
|
|
|
11 = 1 |
+ 3 |
|
|
||||||||||||||
|
|
|
Определим контурные величины. |
22 |
= 2 |
= 12 |
|
||||||||||||||
|
|
|
22 = 2 + 5 |
+ 3 = 2 + 3 + 4 = 9 |
|
||||||||||||||||
|
5. |
|
Запишем |
|
3 22 |
33 = ∞ |
|
33 = 0 |
|
||||||||||||
|
|
|
|
11 11 |
− |
|
− 4 33 = 11 |
|
|
|
|
|
|||||||||
|
|
|
22 22 |
|
контурные уравнения. |
|
|
|
|
|
|||||||||||
|
|
|
− |
3 11 |
|
− 33 5 = 22 |
|
|
|
|
|
||||||||||
|
6. |
|
Определим |
33 |
= |
|
|
|
|
|
|||||||||||
|
|
|
33 |
= |
|
из |
(5)пункта |
|
|
|
|
|
|||||||||
|
|
|
|
10 11 |
|
|
|
контур ые токи. |
|
10 11 − 4 22 = 9 |
|
|
|||||||||
|
|
|
|
− 4 22 = 9 |
|
|
(1) + (2) → |
||||||||||||||
|
|
−4 11 + 9 22 |
|
= 12,6 → 2,5 ∙ (2) |
и→ −10 11 + 22,5 22 = 31,5 → |
||||||||||||||||
1 |
7. |
|
18,5 22 |
|
= 40.5 → 22 ≈ 2,189 |
11 ≈ |
1.776 |
|
|
|
|||||||||||
= 11 |
= 1.776 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
Вернуться к п.3 и подставить значения. |
|
|
|
|
||||||||||||||
= 22 |
= 2,189 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3 |
= 11 |
− |
22 |
= −0.414 |
|
|
|
|
|
|
|||||||||||
4 |
= 11 |
− |
33 |
= 1.576 |
|
|
|
|
|
|
|
|
|||||||||
5 |
= 33 |
− |
22 |
= −1.989 |
|
|
|
|
|
|
|||||||||||
6 |
= 33 |
= 0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
8. |
|
Выполнить проверку по 1 закону Кирхгофа для любого узла. |
|
|||||||||||||||||
1 = 2 |
+ 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
и выходит 2 |
и 3 |
|||||
1.776 |
|
Для проверки выберем узел, в который входит 1 |
|||||||||||||||||||
= |
2,189 − 0.414 − |
|
верно |
|
|
|
|
|
|||||||||||||
|
9. |
|
Записать ответ. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
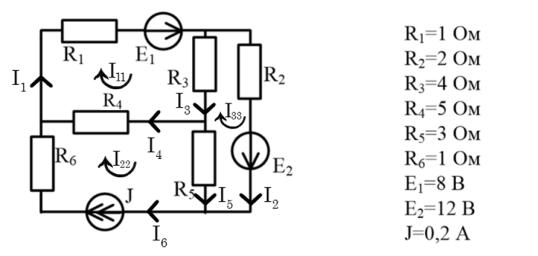
Задача 3. Найти токи во всех ветвях с помощью метода узловых потенциалов.
Дано:
Решение:
1.Определить количество узлов в цепи и количество уравнений в системе, которые нужно построить.
Количество узлов: 4
Количество узлов по 1му закону Кирхгофа: 3 2. Произвольно выбрать узел, потенциал которого принимается за «0».
|
Заземлим узел |
|
|
|
|
|
|
|
|
||||||
|
|
11 |
= 11 |
+ 14 + 0 = 1.2 |
|
|
|
|
|
||||||
3. |
Записать |
узловые уравнения, с использованием узловых величин. |
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|||||
|
|
33 |
|
22 − заземлили |
|
11 |
|
|
|
||||||
|
|
= 3 + |
4 |
+ |
5 = 0.783 |
|
|
1 |
|
||||||
|
|
|
|
|
1 |
|
|
1 |
|
1 |
|
|
|
= −7.8 |
|
|
|
44 |
= 12 |
+ |
15 |
+ 0 = 0.833 |
|
= − 1 |
|||||||
|
|
|
33 |
= 0 |
|||||||||||
|
13 |
|
|
31 |
= − |
1 |
|
44 = 22 |
− |
= 5.8 |
|||||
|
|
|
|
= |
|
4 = −0.2 |
|
|
|
|
|
||||
|
|
|
|
|
41 |
= 14 |
= 0 |
|
|
|
|
|
|||
1 11 |
43 = 34 |
= − 15 = −0.333 |
|
|
|
|
|
||||||||
+ 3 13 |
|
+ 4 14 |
= 11 |
|
|
|
|
|
|||||||
1 31 |
+ 3 33 |
|
+ 4 34 |
= 33 |
|
|
|
|
|
||||||
1 41 |
+ 3 43 |
|
+ 4 44 |
= 44 |
|
|
|
|
|
||||||
4. Решить узловые уравнения относительно потенциалов узлов.
6

|
|
|
|
|
|
1 |
∙ 1.2 − 3 ∙ 0.2 + 4 ∙ 0 = −7.8 |
|
→ |
|||||||||||||||||||||||||
|
|
|
|
|
−1 |
∙ 0.2 + 3 |
∙ 0.783 − 4 ∙ 0.333 = 0 |
|||||||||||||||||||||||||||
|
1.2 |
−0.2 |
|
1 ∙ 0 − |
30.333 + 40.833 = 5.8 |
0.2 |
|
|||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
−7.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
идобавимк2 → |
||||||||||||
|
−0.2 |
0.783 |
−0.333 |
|
0 |
|
→ Умножим1 строкуна |
|
||||||||||||||||||||||||||
|
|
0 |
−0.333 |
.833 |
|
5.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2 |
|
|||||||||||
|
1.2 |
−0.2 |
|
0 |
|
|
|
|
−7.8 → Умножим2 строкуна 0.333 идобавимк 2 → |
|||||||||||||||||||||||||
|
0 |
|
0.75 |
|
−0.333 |
|
−1.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.75 |
|
||||||||
|
0 |
−0.333 |
|
0.833 |
|
|
|
5.8 |
|
|
|
−7.8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1.2 |
−0.2 |
|
|
|
|
|
0 |
|
|
|
|
|
→ Получаемискомыезначения → |
||||||||||||||||||
|
|
|
0 |
0.75 |
|
−0.333 |
|
|
−1.3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
0 |
|
0 |
|
|
0.685 |
|
|
5.223 |
|
= 7,623 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
= 1,652 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
= −6,75 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= 0 |
|
|
|
|
|
|
|
|
|
|
||||
5. |
Отметить токи на схеме (так же, как в задаче 1). |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
1 |
= |
|
12 |
+ 1 |
= |
|
1 |
− 2 |
+ 1 |
|
= 1,775 |
|
|
||||||||||||||||
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Найти токи с помощью закона Ома. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
24+ 1 |
|
21− 4+ 2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
= |
|
|
|
|
= |
- |
= |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
= 233 |
= 2−3 3 |
1,575 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
= |
314 |
= 3−4 1 |
|
|
|
|
2,1885 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=-1,99 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
0,413 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
= |
|
345 = |
|
= |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3−5 4 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 = = 0.2 |
|
|
|
|
|
|
|
|
||||||||
7. Выполнить проверку по I закону Кирхгофа. |
0.413 |
|
|
|
|
|||||||||||||||||||||||||||||
8. |
1 |
= 2 + 3 |
|
|
|
|
|
|
|
|
1.775 = 2.1885 − |
|
|
|
|
|||||||||||||||||||
|
Проверим 2 узел по закону Кирхгофа: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
- выполняется
Записать ответ.
7
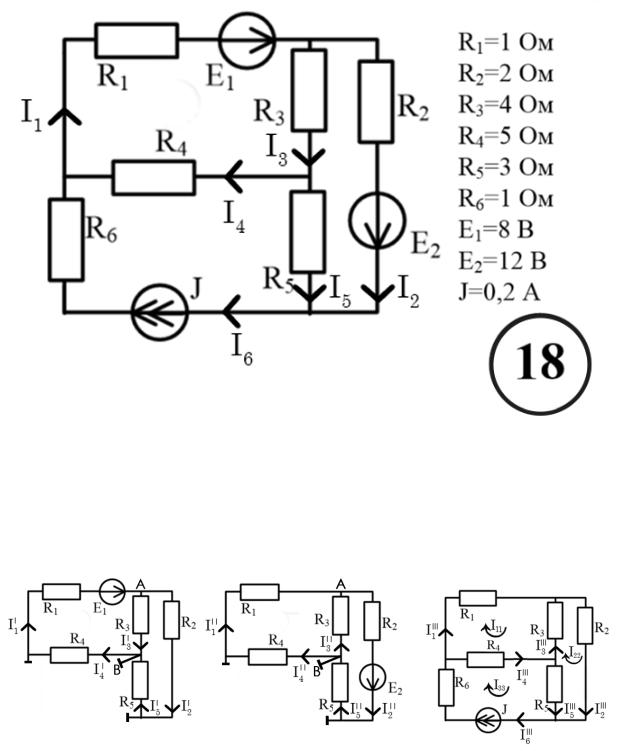
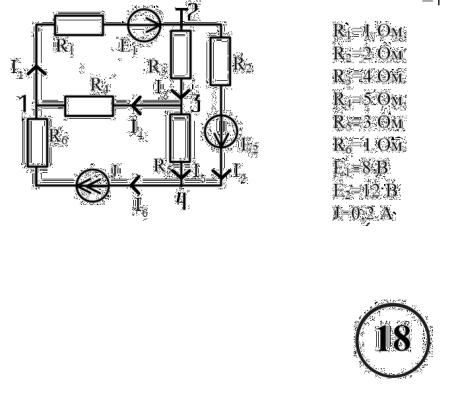
Задача 4. Найти токи во всех ветвях с помощью метода наложения.
Дано:
Решение:
1.Расставить токи на исходной схеме (так же, как в задаче 1). Определить количество частных схем.
Расставила направления токов в ветвях как в 1 задаче и определила 3 частные схемы.
2.Вычертила нужное количество частных схем и расставила токи на частных схемах исходя из направлений источников питания.
Схема E1 |
Схема E2 |
Схема J |
3.Рассчитала токи в частных схемах и выполнила проверку токов в каждой частной схеме по первому закону Кирхгофа
Схема E1 – метод 2 узлов
8
1. |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Найдем напряжение АВ |
|
|
|
||||||||||||||||||||||||||
= |
|
|
|
|
|
1 + 4 |
|
+ |
= 2,162 |
||||||||||||||||||||
|
|
|
|
|
+ |
|
|
+ |
|
|
+ |
|
|
|
|||||||||||||||
2. |
|
|
|
|
|
3 |
|
2 |
|
|
|
5 |
|
|
|
|
1 |
|
|
|
4 |
|
|
||||||
|
|
′1 |
= ′4 |
= |
− + 1 |
= 0,973 |
|||||||||||||||||||||||
|
|
|
1 |
+ 4 |
|
||||||||||||||||||||||||
|
|
Найдём1 |
токи1 |
в схеме |
1 |
|
|
|
|
||||||||||||||||||||
|
|
|
′2 |
= ′5 |
= |
|
|
|
|
|
= 0,432 |
||||||||||||||||||
|
|
|
2 |
+ 5 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
′3 |
= |
3 |
|
= 0,56 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
′3 |
+ ′5 |
|
= ′4 |
по′6 |
= 0 |
|
|
|
|
|
|
|
|
||||||||||||||||
|
→ 0,56 + 0,432 − 0,973 = 0,019 − погрешность |
||||||||||||||||||||||||||||
3. |
Проверка |
|
|
|
закону Кирхгофа для узла В |
||||||||||||||||||||||||
1. |
|
|
|
|
|
|
|
|
|
|
− |
2 |
2 |
|
|
5 |
|
|
|
|
|
Схема E2 – метод 2 узлов |
|||||||
Найдем напряжение АВ |
|
|
|
||||||||||||||||||||||||||
|
|
= |
|
1 |
|
|
|
|
|
|
|
|
|
+ |
|
|
1 |
|
|
= −3,892 |
|||||||||
2. |
|
токи в1схеме |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
+ |
|
||||||||||
|
|
Найдём3 + |
|
2 |
|
|
|
5 + |
|
1 |
|
|
|
4 |
|
||||||||||||||
|
|
|
|
|
′′1 = ′′4 |
= |
|
|
|
− |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
+ 4 = 0,649 |
|||||||||||||||||||||
|
|
|
|
|
′′2 |
= ′′5 = |
|
|
+ 2 |
= 1,622 |
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
+ 5 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
′′3 |
|
= − |
|
3 |
|
|
= 0,973 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3. |
|
Проверка по |
|
′′6 = 0 |
|
|
|
|
|
|
|||||||||||||||||||
′′3 + ′′4 = ′′5 |
→ 0,973 − 1,622 + 0,649 = 0 − погрешность |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
законуКирхгофа для узла В |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
′′′1 |
= 11 |
|
|
|
|
|
|
|
Схема J – метод контурных токов |
||||||||||
|
|
1. Запишем выражения для токов в ветвях через контурные токи. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
′′′2 |
= 22 |
11 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
′′′3 |
= 22 |
|
− |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
′′′4 |
= 33 |
|
− |
11 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
′′′5 |
= 33 |
− |
22 |
|
|
|
|
|
|
||||||||||||
|
|
2. |
|
|
|
′′′6 |
= 33 |
= |
0,2 |
|
|
|
|
|
|
||||||||||||||
|
|
11 |
= 1 |
+ 3 |
|
+ 4 = 1 + 4 + 5 = 10 |
|||||||||||||||||||||||
|
|
|
|
|
Определим контурные величины. |
||||||||||||||||||||||||
|
|
22 = 2 + 5 |
+ 3 |
= 2 + 3 + 4 = 9 |
|||||||||||||||||||||||||
|
|
|
|
11 |
= 1 |
= 0 33 |
= ∞ |
|
|
|
|||||||||||||||||||
|
|
|
22 |
= 2 |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
3. |
|
|
|
|
33 |
= 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Запишем контурные уравнения. |
|||||||||||||||||||||||||
9
|
|
11 11 |
− |
3 |
22 |
− 4 33 |
= 11 |
|
|
|
||||||||||
|
|
22 22 |
− |
3 11 |
− 33 5 |
= 22 |
|
|
|
|||||||||||
|
4. |
Определим |
33 |
= |
|
|
|
|
|
|||||||||||
|
|
33 = |
|
из |
(5)пункта |
|
|
|
|
|||||||||||
|
|
|
10 11 |
− |
контур ые токи. |
→ |
10 11 − 4 22 = 9 |
→ (1) + (2) → |
||||||||||||
|
|
4 22 |
= 1 |
|
→ 2,5 ∙ (2)и |
|||||||||||||||
|
|
−4 11 |
|
+ 9 22 |
= 0,6 |
≈ 0,135 |
|
−10 + 22,5 22 = 1,5 |
|
|||||||||||
|
5. |
18,5 22 |
= 2,5 → |
22 |
11 ≈ 0,154 |
|
||||||||||||||
|
|
|
|
′′′1 |
= 11 |
= 0,154 |
|
|
|
|
||||||||||
|
|
Вернуться к п. и подставить значения. |
|
|||||||||||||||||
|
|
|
|
′′′2 |
= 22 |
= 0,135 |
|
|
|
|
||||||||||
|
|
|
′′′3 = 22 |
− |
11 |
= −0,019 |
|
|
|
|||||||||||
|
|
′′′4 |
|
= 33 |
|
− 11 |
= 0,046 |
|
|
|
||||||||||
|
|
|
′′′5 |
|
= 33 |
|
− 22 |
= 0,065 |
|
|
|
|||||||||
|
|
|
|
′′′6 = 33 |
= 0,2 |
|
|
|
|
|||||||||||
′′′3 + ′′′5 = ′′′4 → |
|
0,046 −0,065 + 0,019 = 0 − погрешность |
|
|||||||||||||||||
|
6. Проверка по закону Кирхгофа |
|
|
|
||||||||||||||||
4. |
1 |
= ′1 |
+ ′′1 |
+ ′′′1 |
= 0,973 + 0,649 + 0,154 = 1,776 |
|
||||||||||||||
Определить токи на исходной схеме с применением принципа суперпозиции токов. |
||||||||||||||||||||
|
2 |
= ′2 |
+ ′′2 |
+ ′′′2 |
= 0,432 + 1,622 + 0,135 = 2,189 |
|
||||||||||||||
|
3 |
= ′3 |
− |
3 |
− |
′′3 |
= 0,56 − 0,973 − |
(−0,019) = −0.394 |
|
|||||||||||
|
4 |
= ′4 |
+ ′′4 |
− |
|
′′′4 |
= 0,973 + 0,649 − 0,046 = 1,557 |
|
||||||||||||
|
5 |
= −′5 − ′′5 |
|
+ ′′′5 = −0,432 − 1,622 + 0,065 = −1,989 |
|
|||||||||||||||
5. |
6 |
= ′6 |
+ ′′6 |
+ ′′′6 |
= 0 + 0 + 0,2 = 0,2 |
|
||||||||||||||
6.4 |
+ 5 |
= 3 |
→ 1,557 − (−0,432) − 2,008 = −0,019 − погрешность |
|||||||||||||||||
|
Выполнить проверку полученных токов по первому закону Кирхгофа. |
|||||||||||||||||||
Записать ответ.
10
