6.1.4. Невизначені, визначені інтеграли: поняття та застосування

Інтегра́л (від лат. integer — цілий) — узагальнення поняття суми нескінченного числа нескінченно малих доданків. Одне з найважливіших понять математичного аналізу, центральне поняття інтегрального числення, застосовується для розв'язання задач:

• обчислення площі під кривою;

• пройденого шляху за нерівномірного руху;

• маси неоднорідного тіла, і таке інше;

• відновлення функції за її похідною (невизначений інтеграл).

Визначений інтеграл — у математичному аналізі це інтеграл функції з вказаною областю інтегрування. Визначений інтеграл є неперервним функціоналом, лінійним по підінтегральних функціях і адитивним по області інтегрування. У найпростішому випадку область інтегрування — це відрізок числової осі. Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.

Визначений інтеграл дорівнює площі криволінійної фігури, обмеженої кривою.

Подальші узагальнення поняття дозволяють розширити його на кратні, поверхневі, об'ємні інтеграли, а також на інтеграли на об'єктах ширшої природи з мірою. Існує кілька різновидів визначених інтегралів: інтеграл Рімана, інтеграл Лебега, інтеграл Стілтьєса, інтеграл Даніелла тощо.

Невизначений інтеграл для функції f — це сукупність усіх первісних цієї функції.

Завдання диференціального числення — обчислення похідної від заданої функції y = f(x). Завдання інтегрального числення протилежне: потрібно визначити функцію, похідна від якої відома. Основоположними поняттями інтегрального числення, є поняття первісної та невизначеного інтегралу.

Застосування невизначених інтегралів

• у задачах про обчислення швидкості або прискорення руху тіла;

• у задачах про обчислення визначених інтегралів (див. формулу Ньютона-Лейбніца);

• для розв'язання диференціальних рівнянь.

6.1.5. Функції багатьох змінних. Частинні похідні. Необхідні і достатні умови екстремуму, умовного екстремуму

Числення багатьох змінних або аналіз функцій багатьох змінних — це область математичного аналізу, що є продовженням теорії обчислення із однією змінною до випадку обчислення функцій із багатьма змінними: диференціювання і інтегрування функцій, що мають багато змінних, а не одну.

Методи аналізу функцій багатьох зміних використовуються для вивчення різних об’єктів і явищ матеріального світу. Зокрема,

Рівняння, що містять часткові похідні, називають рівняннями в часткових похідних, і вони часто використовуються у фізиці, інженерії та інших науках і прикладних дисциплінах.

Часткові похідні застосовуються в рівняннях термодинаміки, таких як рівняння Гіббса-Дюгема, а також в інших рівняннях математичної фізики.

Масштабування зображення. Часткові похідні є одним із ключовим елементів в алгоритмах масштабування зображень до бажаного розміру. Широко відомий алгоритм, який називається англ. seam carving, потребує аби кожному пікселю зображення було приписане деяке числове значення 'енергії', яке описує їх відмінність від ортогонально суміжних пікселів. Алгоритм поступово убирає рядки або стовпці з найменшою енергією. Формула, що обирається для визначення енергії пікселя (величина градієнта в пікселі) здебільшого використовує для побудови часткові похідні.

Екстремум — найбільше або найменше значення функції на заданій множині. Розрізняють:

• лока́льний — екстремум у певному довільно малому околі даної точки;

• глоба́льний — екстремум в усій розглядуваній області значень функцій.

Задачі знаходження екстремуму виникають у всіх галузях людського знання: теорії автоматичного керування, економіці, біології, фізиці тощо.

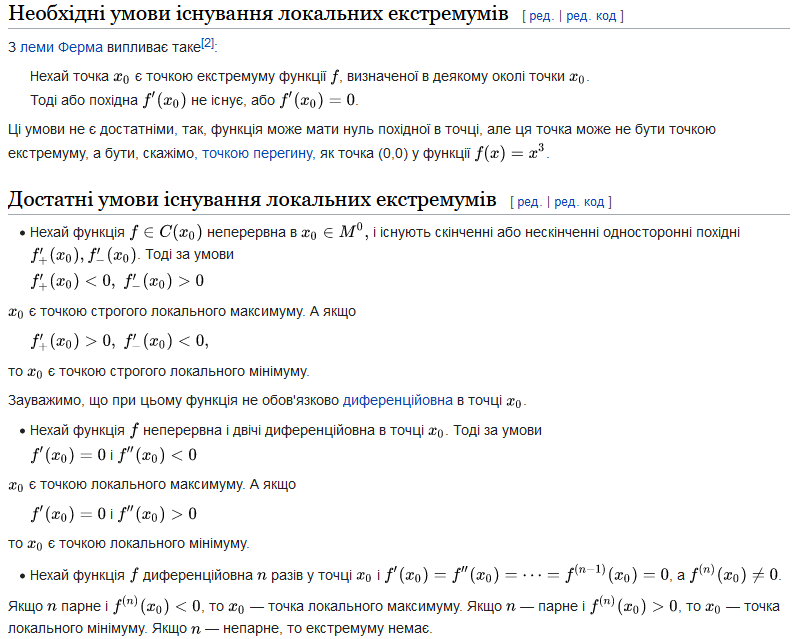
Перша достатня умова екстремуму. Якщо функція диференціюється в точці і перша похідна функції змінює знак при переході через точку , то функція досягає в цій точці екстремуму, причому:

1. – точка максимуму, якщо знак змінюється з плюса на мінус;

2. – точка мінімуму, якщо знак змінюється з мінуса на плюс.

Друга достатня умова екстремуму. Якщо функція двічі диференціюється в точці , причому перша похідна функції дорівнює нулю, а друга похідна відмінна від нуля ( , ), то функція досягає в цій точці екстремуму, причому:

1. – точка максимуму, якщо ;

2. – точка мінімуму, якщо .

Точки, в яких функція досягає максимального або мінімального значення, називаються точками екстремуму, а значення функції в точці екстремуму називається екстремумом функції.

В математичній оптимізації, умовна оптимізація — це процес оптимізації цільової функції щодо деяких змінних за наявності обмежень на ці змінні. Цільова фукнція це або функція втрат або функція енергії, яку треба мінімізувати, або функція винагороди або функція корисності, яку треба максимізувати. Обмеження це або жорсткі обмеження, які встановлюють умови на змінні, які мають бути дотримані, або м'які обмеження, які встановлють штрафи на деякі значення змінних в цільовій функції, якщо (і наскільки) ці обмеження не дотримані.