§ 4. Умовна ймовірність

Ймовірність події може змінитися, якщо відбулась деяка інша подія. Розглянемо приклад.

Нехай в урні 10 куль, з них 3 білих і 7 чорних. Навмання беруть дві кулі. Подія А - взята біла куля, подія В - взята чорна куля.

Якщо кулю, взяту першою, повертають до урни, то ймовірність появи другої кулі не залежить від того, яка взята перша куля.

Якщо перша куля не повертається до урни, то ймовірність другої події залежить від результату першого випробування. Якщо першою взяли білу кулю, то в урні залишилося 2 білих кулі та 7 чорних, тому ймовірність взяти чорну кулю дорівнює 7/9.

Якщо першою взяли чорну кулю, то в урні залишилось 3 білих та 6 чорних куль, тому ймовірність взяти чорну кулю дорівнює 6/9.

Отже, ймовірність події В залежить від появи або не появи події А.

Означення 10.13. Імовірність події В, обчислена при умові появи події А, називається умовною ймовірністю події В і позначається Р(В\А) або Р_А(В).

Теорема 10.5. Імовірність добутку двох подій А і В дорівнює добутку ймовірності події А на умовну ймовірність події В за умови, що подія А відбулася, тобто

Р(АВ) = Р(А)-Р(В\А). (7)

Доведення. Позначимо через п кількість усіх можливих випадків, через т - кількість випадків, що сприяють події А, через k - кількість випадків, що сприяють події АВ. Тоді

що і доводить формулу (7). Теорему доведено.

Теорема 10.6. Умовна ймовірність обчислюється за формулою

Теорема 10.7. Для двох подій А і В має місце рівність

Р(А)Р(В \ А) = Р(В)Р(А \ В). (9)

Доведення теореми 10.7 випливає з рівності АВ=ВА і формули (7).

Означення 10.14. Дві події А і В називаються незалежними, якщо припущення, що відбулась одна з них, не змінює ймовірності другої.

З означення 10.14 випливає, що для незалежних подій виконуються такі рівності

Р(В\А) = Р(В), Р(А \ В) = Р(А). (10)

Для встановлення незалежності подій А і В досить переконатися у виконанні однієї з рівностей (10), оскільки друга випливає як наслідок. Нехай виконується перша рівність (10). Поділивши обидві частини рівності (9) на Р(В) = Р(В\А), дістанемо другу рівність (10).

Аналогічно з другої рівності (10) виводимо, як наслідок, першу рівність.

Означення 10.15. Події А₁, А₂,..., А_п називаються незалежними у сукупності, коли вони попарно незалежні і будь-який добуток цих подій (що містить у собі не всі їх) з кожною подією, що не ввійшла до цього добутку, незалежний.

Теорема 10.8. Імовірність добутку двох незалежних подій дорівнює добутку їх імовірностей - тобто коли події А і В незалежні, то

Р(АВ) = Р(А)Р(В). (11)

Доведення. З рівностей (7) і (10) маємо:

Р(АВ) = Р(А) • Р{В \ А) = Р(А) • Р(В),

що і треба було довести. Наслідком цієї теореми є наступна теорема.

Теорема 10.9. Якщо події А₁, А₂,..., А_п незалежні у сукупності, то

Р(А₁А₂...А_п) = Р(А₁).Р(А₂),...,Р(А_п). (12)

Приклад 10.7. Яка ймовірність того, що при киданні трьох гральних кубиків число 5 випаде хоч на одному з них?

Розв'язання. Для кожного грального кубика ймовірність випадання п'ятірки дорівнює 1/6. Тоді ймовірність не випадання п'ятірки дорівнює 1 — 1/6 = 5/6. Невипадання п'ятірки для трьох гральних кубиків є події, незалежні в сукупності, тому за формулою (12) ймовірність невипадання жодної п'ятірки

Теорема 10.10. Нехай випадкова подія А може з'явитися лише сумісно з однією із несумісних між: собою подій В₁, В₂,..., В_п, які утворюють повну систему подій. Тоді має місце формула

Доведення. За умовою теореми поява події А означає появу однієї з подій АВ_1, АВ₂,..., АВ_п, тобто А = АВ₁ + АВ₂ +...+ АВ_п.

Події В₁, В₂,..., В_п несумісні, тому і події АВ₁, АВ₂,..., АВ_п також несумісні. За теоремою додавання ймовірностей несумісних подій маємо

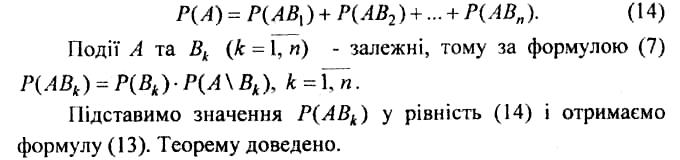
Події В_1, В₂,..., В_п називають гіпотезами для події А.

Приклад 10.8. У магазин привезли сорочки з трьох фабрик: 50% - з першої фабрики, 30% - з другої і 20% - з третьої. Брак першої фабрики складає 2%, другої - 3%, третьої - 5%. Яка ймовірність того, що куплена в магазині сорочка якісна?

Розв'язання. Нехай подія А - куплена сорочка якісна. Можливі три гіпотези В_ь В₂, В₃ - куплена сорочка відповідно першої, другої або третьої фабрики. Вони утворюють повну систему подій, причому Р(В_]) = 0,5, Р(В₂) = 0,3, Р(В₃) = 0,2.

Відповідні умовні ймовірності події А дорівнюють

В умовах теореми 10.10 невідомо, з якою подією із несумісних подій В₁, В₂,..., В„ з'явиться подія А. Тому кожну з цих подій вважають гіпотезою, а Р(В_к) - ймовірність k - ої

гіпотези, k = 1,п.

Якщо випробування проведено і в результаті того подія А з'явилася, то умовна ймовірність Р(В_к \А) може не дорівнювати Р{В_к). Для одержання умовної ймовірності Р(В_к\А) використаємо теорему множення ймовірностей залежних подій:

Підставивши у рівність (15) замість Р(А) її значення з формули (13), одержимо

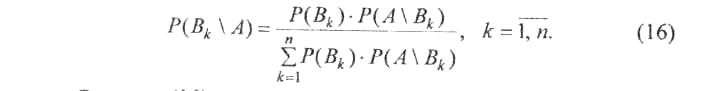
Формули (16) називають формулами Байєса (Т. Байєс (1702-1761) - англійський математик). Вони дозволяють переоцінювати ймовірність гіпотез. Це важливо при контролі або ревізіях.

Приклад 10.9. Виготовлені цехом заводу деталі потрапляють на перевірку їх стандартності до одного з двох контролерів. Ймовірність того, що деталь потрапить до першого контролера, дорівнює 0,6, а до другого - 0,4. Ймовірність того, що деталь буде визнана стандартною першим контролером, дорівнює 0,94, а другим - 0,98.

При перевірці деталь визнана стандартною. Яка ймовірність того, що цю деталь перевіряв перший контролер?

Розв'язання. Позначимо А подію: деталь визнана стандартною; В_х - деталь перевіряв перший контролер; В₂ -деталь перевіряв другий контролер. За умовою

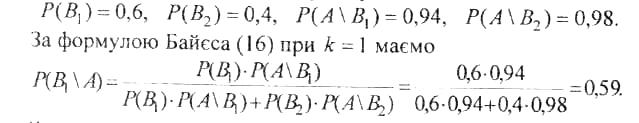
Зауважимо, що до появи події А імовірність P(B_l) = 0,6, a після появи події А імовірність перевірки деталі першим контролером Р(В_[ \ А) = 0,59, тобто зменшилась.