
Министерство цифрового развития, связи и массовых коммуникация Российской Федерации
Ордена Трудового Красного Знамени федеральное государственное бюджетное
образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра Информатики
Лабораторная работа №6
По дисциплине «Численные методы»
На тему «Одномерная оптимизации»
Вариант 23
Выполнил: студент группы
Проверил: преподаватель
Москва, 2024
Цель работы
1. Выбрать индивидуальное задание по номеру варианта из табл. 5-1 для решения задачи одномерной оптимизации:
• функцию f(x), минимум которой необходимо найти;
• метод золотое сечение – четные номера п.3, нечетные –п.4
• метод дихотомии - четные номера п.4, нечетные –п.3
2. Провести исследование индивидуального варианта задания:
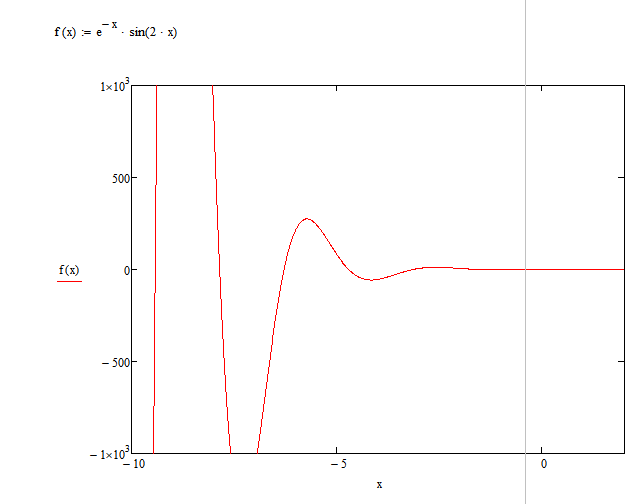
• построить
график функции
![]()
• выбрать начальный отрезок неопределенности (отрезок, содержащий точку минимума);
• проверить выполнение необходимого и достаточного условий унимодальности функции на выбранном отрезке.
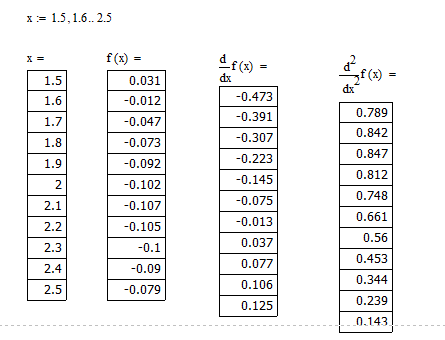
3. Создать в сценарии функцию для проведения значений 3-х итераций определить длину отрезка, содержащего точку минимума, после трех итераций.
4. Написать и выполнить программу, реализующую программу метода, вычисляющую координаты точки минимума функции с заданной точностью 10^-4 .
5. Вычислить число итераций, необходимых, чтобы локализовать точку минимума с точностью E1 = 10^-4 методами дихотомии и золотого сечения.
6. Решить задачу оптимизации с использованием функции optim пакета Scilab.
Индивидуальное задание
![]()
Золотое сечение - расчет на ПК
Дихотомия - ручной расчет
Выполнение задания
Часть 1 - ручной расчет - Дихотомия
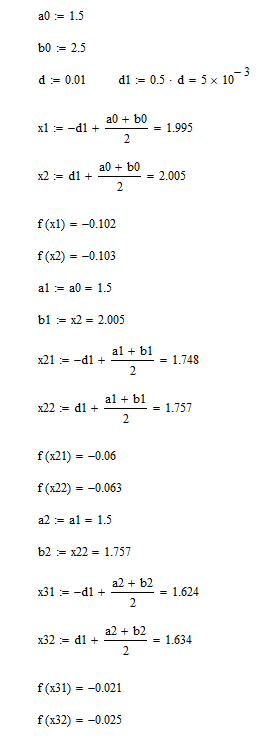
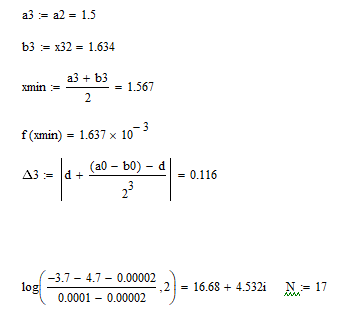
n |
a |
b |
X1 |
X2 |
F(x1) |
F(x2) |
Δ |
1 |
1.5 |
2.5 |
1.995 |
2.005 |
-0.102 |
-0.103 |
0.001 |
2 |
1.5 |
2.005 |
1.748 |
1.757 |
-0.06 |
-0.063 |
0.003 |
3 |
1.5 |
1.757 |
1.624 |
1.634 |
-0.021 |
-0.025 |
0.004 |
4 |
1.5 |
1.634 |
|
|
|
|
|
Часть 2 - расчет на ПК - Золотое сечение
import math
def f(x):
funс = math.exp(-x) * math.sin(2*x)
return funс
def zoloto(a, b, E):
n = 0
k1 = (3 - math.sqrt(5)) / 2
k2 = (math.sqrt(5) - 1) / 2
x1 = a + k1 * (b - a)
x2 = a + k2 * (b - a)
F1 = f(x1)
F2 = f(x2)
while abs(b - a) > E:
n += 1
if F1 < F2:
b = x2
x2 = x1
x1 = a + k1 * (b - a)
F2 = F1
F1 = f(x1)
else:
a = x1
x1 = x2
x2 = a + k2 * (b - a)
F1 = F2
F2 = f(x2)
print(n, a, b, x1, x2, f(x1), f(x2), abs(a - b))
xmin = (a + b) / 2
fxmin = f(xmin)
return xmin, fxmin
a = 1.5
b = 2.5
eps = 0.0001
xmin, fxmin = zoloto(a, b, eps)
print("Минимум для x:", xmin)
print("Минимум для f(x):", fxmin)
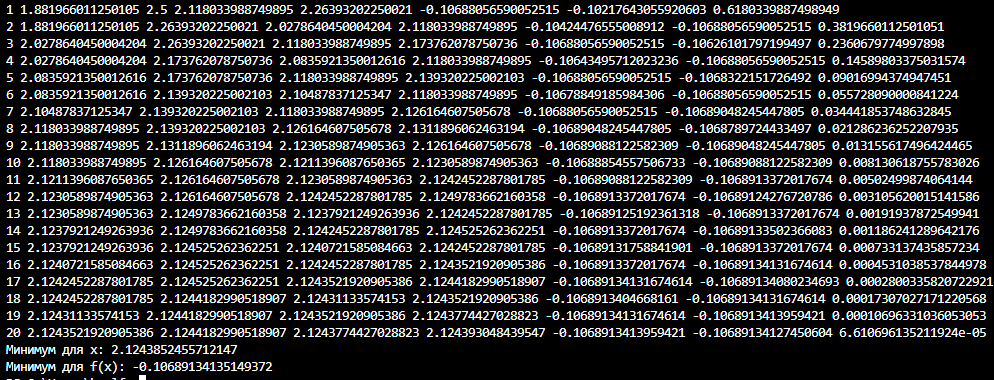
При N=17 длина отрезка 0.00028
Точность достигнута при 20 итерациях
Схема работы алгоритма
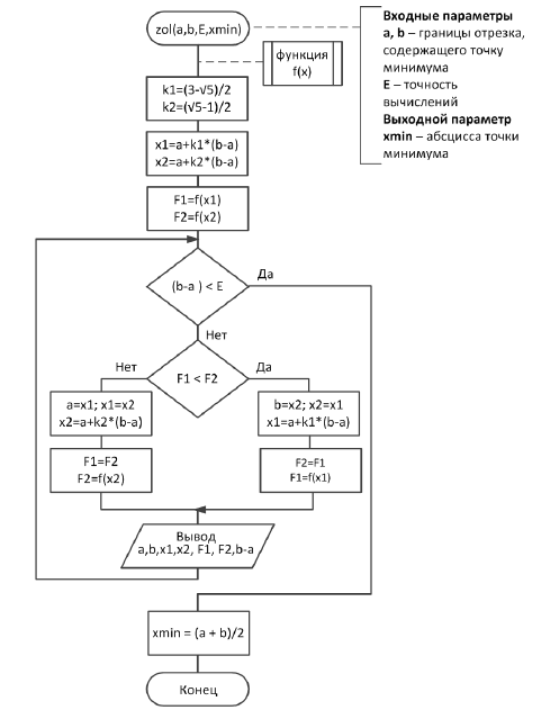
Вывод
В данной работе мною была изучена одномерная оптимизация и выполнено задание не ручной расчет и расчет на ПК
