Методика преподавания математики

1. Методика обучения решению задач на доказательство, вычисление и построение в

курсе планиметрии.

Задача на доказательство:

Пример. Задача. В треугольниках АВС и А1В1С1 углы А и А1 – прямые, BD и B1D1 – биссектрисы. Докажите, что треугольники равны, если угол В равен углу В1 и BD=B1D1.

Задача на вычисление:

1 этап. Основной метод – вопросно–ответный (беседа).

– Какие геометрические фигуры рассматриваются в задаче? (Равнобедренный прямоугольный треугольник и квадрат).

– Выясним, как они расположены относительно друг друга. Для этого вспомните, какими свойствами обладает равнобедренный прямоугольный треугольник? (Катеты равны, угол прямой). Квадрат? (Углы прямые и стороны равны).

– В обозначении квадрата использована буква С, что это значит? (Одна вершина квадрата и вершина прямоугольного треугольника с прямым углом при ней совпадут в точке С).

– Что сказано о трех других вершинах квадрата? (Е – на гипотенузе, а D, F – должны лежать на катетах, потому, что по условию стороны квадрата с общей вершиной С лежат на катетах)

Параллельно строится чертеж, оформляется краткая запись.

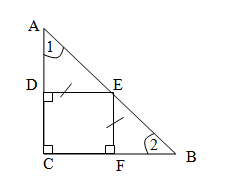
2 этап.

Аналитический метод поиска решения:

– Какие величины даны в условии? (Длина катета треугольника). Что надо найти в задаче? (Периметр квадрата)

– По какой формуле он рассчитывается? (Р=4а).

–А что для этого надо знать? (Длину стороны квадрата).

– Частью каких элементов треугольника являются стороны квадрата? (Частью сторон).

– Можно ли визуально предположить, как связаны стороны треугольника и стороны квадрата? (Видимо, равны половине стороны). Если бы нам удалось это доказать, смогли бы мы ответить на вопрос задачи? (Да. 6 умножить на 4).

– Итак, надо попытаться доказать, что сторона треугольника равна по длине двум сторонам квадрата. Одна сторона квадрата непосредственно является частью стороны треугольника. Значит нужно доказать, что оставшаяся часть FB равна стороне квадрата.

– В состав какой фигуры входит отрезок FB? (DEFB). Может быть, можно визуально найти равный ему треугольник, в состав которого входит сторона квадрата? (DADE, сторона DE).

– Итак, нужно доказать равенство треугольников. Что мы можем сказать о виде треугольников? ( они прямоугольные). Какие признаки равенства прямоугольных треугольников знаем? Какие равные элементы имеются в треугольниках? (Два угла соответственно равны и два катета как стороны квадрата).

– Какой можно вывод сделать, опираясь на признак равенства? (Треугольники равны).

– Что из этого следует? (DE=FB).

–Чему равна длина стороны треугольника? (Сумме длин сторон квадрата CB=CF+DE=2CF).

– Чему равна длина стороны квадрата из этого выражения? (Половине длины стороны треугольника).

– Зная длину стороны треугольника, сможем найти сторону квадрата? Периметр?

Намечается общий план решения задачи.

1. Доказать, что треугольники DEFB и DADE – прямоугольные и обосновать их равенство.

2. Сделать вывод о равенстве отрезков DE и FB.

3. Найти длину стороны квадрата.

4. Найти периметр квадрата.

3 этап – осуществление плана во всех деталях, оформление решения.

Решение

1. DEFB и DADE – прямоугольные (при их вершинах D и F углы являются смежными с углами квадрата, тогда их величина по 90°).

2. DEFB=DADE (по катету и острому углу): Ð1=Ð2 как углы при основании равнобедренного треугольника, DE=EF как стороны квадрата.

3. DЕ=FB из равенства треугольников, тогда СВ=CF+FB=CF+DE=2CF. Откуда CF=1/2CВ=6см.

4. Р=6×4=24 (см).

Ответ. 24см.

4 этап. Исследование. Оценка полученного ответа на достоверность: периметр выражается положительным числом, в нашем случае – верно. 

2. Математические понятия и методика их изучения в средней школе. Применение научных методов анализа и синтеза при обучении математике в школе. Применение научных методов индукции и дедукции при обучении математике в школе.

Характеристика основных этапов изучения математических понятий

Методика работы над определением предполагает:

1) знание определения;

2) обучение распознавания объекта, соответствующего данному определению;

3) построение различных контрпримеров.

Изучение математических определений можно подразделить на три этапа:

1-й этап – введение – создание на уроке ситуации, когда учащиеся либо сами “открывают” новое, самостоятельно формируют для них определения, либо просто подготавливаются к их пониманию.

2-й этап – обеспечение усвоения – сводится к тому, чтобы школьники:

а) научились применять определение;

б) быстро и безошибочно запоминать их;

в) понимали каждое слово в их формулировках.

3-й этап – закрепление – осуществляется на последующих уроках и сводится к повторению их формулировок и обработке навыков применения к решению задач.

Ознакомление с новыми понятиями проводятся:

1 способ: учащиеся подготавливаются к самостоятельному формированию определения.

2 способ: учащиеся готовятся к сознательному восприятию, пониманию нового математического предложения, формулировка которого им сообщается затем в готовом виде.

3 способ: учитель сам формулирует новое определение без какой-либо подготовки, а затем сосредотачивает усилия учащихся на их усвоении и закреплении.

1 и 2 способ представляют эвристический метод, 3 способ – догматический. Использование любого из способов должно соответствовать уровню подготовленности класса и опыта учителя.

Знакомство (почему появилось, откуда и когда)

Заучивание (рекомендации как легче запомнить)

Проверка знаний (математический диктант, зачет)

Умение применения (решение задач, проекты и т.д.)

Методика и формы работы (тут хоть и написан прямой пример работы, но так думаю даже пизже для понимания)

Фронтальная работа с классом;

Работа в группах, парах;

Зачёты с привлечением старшеклассников;

Мозговой штурм (при введении нового понятия или при закреплении);

Проектная деятельность (опережающие или итоговые по теме; индивидуальные и групповые)

Расскажу на примере работы с понятием числа и его развитии:

Пятиклассники выполняют действия только с натуральными числами, на множестве которых выполняются не все действия. Нельзя вычесть пять из шести и невозможным является деление этих чисел, а жизненные ситуации требуют их исполнения. Результат – введение целых чисел, а затем рациональных. До восьмого класса дети не догадываются, что есть и другие числа – иррациональные. Необходимость их введения опять обосновывается. И если далее идти по этой цепочке, то учащимся понятно введение нового действия – логарифмирования, поэтому они быстрее усваивают, что такое логарифм числа, им легко работать с этим определением и они осознанно выполняют действия с логарифмами.

В любой параллели в сентябре начинаю уроки с развития числа, радуемся, что, мы поднялись ещё на одну ступеньку и показываю, что по этой цепочке будут изучаться все основные блоки в курсе математики, а именно сначала вводится понятие степени с натуральным показателем, затем с целым и рациональным показателем. Впервые дети изучают уравнения линейные, потом квадратные, а далее дробные и иррациональные. По той же схеме знакомство с неравенствами и функциями. Обязательно даю исторические справки и авторство понятий и определений.

Приведу пример, как работаю с понятием «функция».

Впервые с этим понятием дети знакомятся в седьмом классе. Именно учитель на уроке даёт определение, что такое функция, самим учащимся это будет трудно сделать, хотя конечно подготовка к введению нового понятия проводится. Сообщаю, что в жизни мы часто встречаемся с зависимостями и с соответствиями, например: каждому человеку соответствует имя, возраст, рост и т д, каждой стране – президент, столица, разговорный язык. На конкретных примерах говорим о зависимых и независимых переменных величинах и далее строим математическую модель: каждому числу из одного множества ставится в соответствие число из другого множества по указанному правилу. Так, если каждому числу ставим в соответствие его квадрат, то говорят - задана функция = . Вводится понятие график функции. Для закрепления и контроля использую работу в парах, математический диктант, «найди ошибку» и т.д.

Далее работа с этим понятием встречается в восьмом классе, уже более широко, а именно, рассматриваем свойства функций: область определения, возрастание, убывание функций, симметричность и другие. Ученики знакомятся с квадратичной функцией, обратной пропорциональностью, кубической зависимостью, учатся строить графики этих функций. Не остаются без внимания понятия функция и свойства функций и в девятом, десятом классах. Практически все девятиклассники принимают участие в подготовке проектов « Графики функций, содержащих знак модуль», объединяясь в группы.

В старшей школе при введении понятия «производная функции», провожу «Мозговой штурм», вспоминаем всё, что связано с понятием функция (на доске появляется до пятнадцати терминов), и убеждаемся, что этого недостаточно, чтобы построить график предложенной им функции, и подвожу к необходимости новых сведений – введения нового понятия «производная функция». Дети видят, что поднимаемся на новую ступеньку, где будут выполняться действия уже не с числами, а действия над функциями.

Эта цепочка отлично показывает, как педагог заинтересован в выполнении всех звеньев этой цепи, и какие результаты может получить в конце проделанной работы.

применение дедукции и индукции в обучении математике

Дедукция широко применяется в обучении как одна из основных форм изложения учебного материала. В дедуктивном умозаключении новое знание добывается опосредованно, без обращения к непосредственному опыту. Дедуктивный подход к построению учебного предмета позволяет вместо описания множества отдельных единичных фактов изложить общие принципы, понятия и умения применительно к соответствующей области знания, усвоение которых позволит затем учащимся анализировать все частные варианты как их проявления. Применение дедуктивного метода особенно полезно при изучении теоретического материала, при решении задач, требующих выявления следствий из некоторых более общих положений. Он позволяет учащимся раньше усваивать знания общего и абстрактного характера и уже из них выводить более частные и конкретные знания. Это открывает большие возможности для сокращения объёма учебного материала и времени, необходимого для его усвоения.

Применение индукции в обучении позволяет сделать обобщающий вывод очевидным, убедительным, вытекающим из рассмотренных фактов и потому доказательным для учащихся. Наиболее, широко индукция применяется в опытных науках и соответствующих им учебных предметах. В старших классах к индукции прибегают в тех случаях, когда нужно показать общую закономерность для всех явлений какой-то группы, но доказательства этого положения предложить учащимся ещё нельзя.

Слабость индуктивного метода обучения состоит в том, что они требуют большего времени на изучение нового материала, чем дедуктивные. Они в меньшей мере способствуют развитию абстрактного мышления, так как опираются на конкретные факты, опыты и другие данные. Однако возможность получения с помощью индукции ложного заключения не является основанием для отрицания роли индукции в школьном обучении. Во-первых, применение индукции в учении корректируется и направляется учителем к открытию истин. Во-вторых, нужно добиваться понимания учащимися правдоподобного характера индуктивного заключения. Поэтому, применяя индукцию, необходимо всячески подчеркивать, что заключение является лишь предположением, гипотезой, которое может быть доказано (если оно истинно) или опровергнуто (если оно ложно).

Различают два основных вида индукции: неполную и полную. Неполная индукция (как метод исследования) – индукция, при которой не исчерпываются все частные случаи, относящиеся к данной ситуации. Неполной индукцией называется вывод, основанный на рассмотрении одного или нескольких (но не всех) единичных или частных суждений, относящихся к рассматриваемому понятию (или системе понятий). Вывод, основанный на неполной индукции, может быть ошибочным, поэтому индукция в качестве метода исследования применяется весьма осторожно. Значение неполной индукции состоит в том, что рассмотрение частных случаев позволяет выявить закономерность, помогает высказать гипотезу о характере этой закономерности; доказательство же должно быть осуществлено другим путем (обычно дедукцией). В процессе обучения школьников к неполной индукции нужно относиться осторожно, учащиеся должны знать, что заключения по индукции могут быть и ложными, и истинными, они нуждаются в доказательстве. Но пренебрегать неполной индукцией нельзя, в этом методе реализуется принцип обучения «от простого к сложному», изучение новых абстрактных понятий и высказываний проходит естественным путем через опыт и наблюдение, через восприятие и представление и т.д. Изучение темы с помощью метода индукции особенно полезно в тех случаях, когда материал носит, преимущественно, фактический характер или связан с формированием понятий, смысл которых может стать ясным лишь в ходе индуктивных рассуждений.

Применение анализа и синтеза в обучении математике

Анализ и синтез являются важнейшими методами обучения школьников. Часто умение мыслить связывают с умением анализировать. Это вполне правомерно, так как вывод следствий, выражающих новые свойства изучаемого объекта, очень часто требует анализа того, что уже известно о нем. В таком понимании, наиболее важном для обучения, анализ является средством поиска решения, доказательства, хотя в большинстве случаев сам по себе решением, доказательством еще не является. Синтез, опираясь на данные, полученные в ходе анализа, дает решение задачи или доказательство теоремы.

Анализ лежит в основе весьма общего подхода к решению задач (имеется в виду нестандартных задач, для которых нет соответствующего алгоритма), известного под названием сведения (редукции) задачи к совокупности подзадач. Идея такого подхода состоит именно в свойственном для анализа «размышлении в обратном направлении» от задачи, которую предстоит решить, к подзадачам, затем от этих подзадач к подподзадачам и т.д., пока исходная задача не будет сведена к набору элементарных задач.

Примером применения анализа и синтеза могут служить арифметический и алгебраический методы решения текстовой задачи. Арифметический метод иллюстрирует синтез, алгебраический – анализ.