Непрерывность некоторых функций.
1) y=c (постоянная) непрерывна в х0 R lim c=c. Зададим ε>0 рассмотрим разность f(x)-f(x0)=c-c=0<ε
xx
x: x-x0< (>0)!
2) y=x непрерывна в x0R, то есть lim x=x0. Зададим ε>0 рассмотрим разность f(x)-f(x0)=x-x0<ε
xx
x: x-x0< (>0)! =ε!
Следствие.
Многочлен p(x)=anxn+ an-1xn-1+…+a1x+a0
(an,an-1…a1,a0 – зададим число)
n=0,1,2,3…. непрерывен в любой точки х0 оси как сумма произведения непрерывной функции. Рациональная функция:
R(x)=p(x)/q(x). Частная двух многочленов непрерывна в любой точки х0 в которой q(x)0
Лекция №9
Ведущая: Голубева Зоя Николаевна
Дата: среда, 11 октября 2000 г.
Тема: «Точки разрыва»
1) Доказать, что lim [((1+x)p-1)/px]=1
x0
y=(1+x)p-1
lim [((1+x)p-1)/px]= x0 y0 =lim ([ln(1+x)]/x)([(1+x)p-1]/[pln(1+x)]=lim ([ln(1+x)]/x)
x0 (1+x)p=y+1 x0 x0
p[ln(1+x)]=ln(y+1)
lim([(1+x)p-1]/[pln(1+x)]=lim y/[ln(y+1)]=1 что и требовалось доказать (1+x)p-1~px при x0
x0 y0 (1+x)p=1+px+o(x) при х0
2) Доказать, что lim (ex-1)/x=1
x0
y=ex-1
lim (ex-1)/x= x0 y0 =lim y/[ln(y+1)]=1 что и требовалось доказать
x0 ex=y+1 y0
x=ln(y+1)
ex-1~x при x0
ex=1+x+o(x) при х0
Классификация точек разрыва функции.
Определение: Пусть y=f(x) определена в О(х0), а в самой точке х0 может быть как и определена, так и неопределенна.
1) Точка х0 называется точкой разрыва 1ого рода функции, если
а) Существует lim f(x)’=lim f(x)’’ , но либо функция неопределенна в точки х0 либо f(x0)b. Тогда точка х0
xx+0 xx-0
точка
устранимого разрыва. 
1,x=1
Y=(x-1)/(x-1)=
Не , x=1
б) f(x)=cb
Можно доопределить или переопределить в точке х0, так что она станет непрерывной.
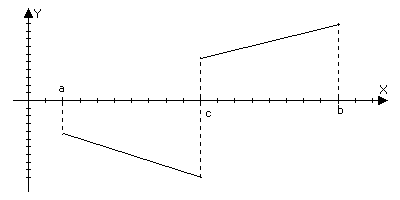
lim f(x)=b; lim f(x)=c, но bc
xx+0 xx-0
Может быть и определена f(x0)=b
Или f(x0)=d
2
)Точка
х0
называется точкой разрыва 2ого
рода функции если она не является точкой
разрыва 1ого
порядка, то есть если хотя бы один из
односторонних пределов не существует
или равен бесконечности.
y=sin(1/x)
Основные теоремы о непрерывных функциях.
Теорема: Все основные элементы функции непрерывны в любой точки своей области определения.
Определение: (функции непрерывной на отрезке)
y=f(x) – называется непрерывной на отрезке [a,b], если она непрерывна в любой точке х(a,b). В точке х=а функция непрерывна справа, то есть lim f(x)=f(a), а в точке х=b функция непрерывна слева lim f(x)=f(b).
xx+0 xx-0
Функция непрерывна на множестве D если она непрерывна в этой точке.
Теорема: (о сохранение знака непрерывной функции)
Пусть y=f(x) непрерывна в точке х0 и f(x0)>0 (f(x0)<0), тогда f(x)>0 f(x)<0 непрерывна в некоторой точки О(х0)
Доказательство: lim f(x)=f(x0) ε>0 >0 x: x-x0< f(x)-f(x0)|<ε.
xx
Пусть f(x0)>0, выберем ε=f(x0) f(x)-f(x0)<f(x0) xO(x0) (>0!)
-f(x0)<f(x)-f(x0)<f(x0); f(x)>0 xO(x0), если f(x0)<0, то ε=-f(x0)
Теорема Коши: ( о нуле непрерывной функции)
Пусть f(x) непрерывна на [a,b] и на концах его принимает значение разных знаков f(a) f(b) <0, тогда x0(a,b): f(x0)=0
Доказательство:
f(b)>0 f(a)<0
Разделим отрезок [a,b] пополам. Если в середине отрезка f(x)=0, то всё доказано, если нет, то выберем ту половину отрезка, на концах которой функция принимает значение разных знаков. Выбранной отрезок поделим пополам. Если в середине нового отрезка f(x)=0, то всё доказано, если нет, то выберем ту половину от той половины, на концах которой функция принимает значение разных знаков и т.д.
[a,b][a1,b1][a2,b2]
Последовательность левых концов удовлетворяет отношению a<a1<a2<…<an<…<b
bb1b2…bn…>a
{
an}-ограниченная
не убывающая
lim
an=b f(a)<0
f(an)<0
n
x+ [anbn]=(b-a)/2n 0 при n
{bn}-ограниченная не возрастающая lim bn= f(b)>0 f(bn)>0 n
x+
В силу непрерывности функции lim f(an)=f (lim bn)=f()0 lim (bn-an)=-= lim (b-a)/2n=0=
x+
x+
x+
x+
f()0
f()=0 x0=
f()=f()0
Условие непрерывности функции нельзя отбросить: f(b)>0; f(a)<0
