
- •Теоретические сведения
- •3. Выполнение лабораторной работы
- •3.1 Получение выборки с генератора
- •3.4.2 Исключение промахов
- •3.4.3 Построение гистограммы
- •3.4.5 Проверка гипотезы о нормальности распределения (критерий ).
- •3.4.6 Расчет значений результата измерений в зависимости от результатов применения критерия Пирсона.
- •4. Выводы
Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего образования «Национальный исследовательский университет
«Московский институт электронной техники»
Институт микроприборов и систем управления
Отчет по лабораторной работе №3
«Обработка результатов измерений с многократными наблюдениями»
Выполнили студенты группы КЕК-$$:
EL_RADIO
EL_BIBA
EL_BOBA
EL_ZELIBOBA
Проверил преподаватель:
Гуркало Кирилл Олегович(ЗАЙКА ЛАПОЧКА)
Содержание
1. Теоретические сведения 3
3. Выполнение лабораторной работы 8
3.1 Получение выборки с генератора 8
3.2 Получение выборки с источника напряжения 8
3.3 Получение выборки без источника напряжения 9
3.4 Обработка выборок с помощью Python 3.x 9
3.4.1 Расчёт параметров выборок 9
3.4.2 Исключение промахов 11
3.4.3 Построение гистограммы 11
3.4.5 Проверка гипотезы о нормальности распределения (критерий ). 17
3.4.6 Расчет значений результата измерений в зависимости от результатов применения критерия Пирсона. 22
4. Выводы 24
Теоретические сведения
Если каждое измерение одной и той же величины дает несколько отличные от других измерений результаты, то имеет место ситуация, когда случайная погрешность играет существенную роль. При необходимости определения случайной составляющей погрешности измерение следует производить несколько раз. В этом случае выполняют измерения с многократными наблюдениями.
Наблюдение - экспериментальная операция, выполняемая в процессе измерений, в результате которой получают одно значение из группы значений величины, подлежащих совместной обработке для получения результата измерения.
Совокупность результатов наблюдений, полученных в процессе одного измерения, называется выборкой наблюдений.
Сами результаты наблюдений могут быть получены в процессе выполнения измерения любого вида (прямые, косвенные, совокупные, совместные) как по методу непосредственной оценки, так и по методу сравнения с мерой.
Результаты измерений с многократными наблюдениями, как и сами наблюдения, являются случайными величинами, поскольку имеют погрешности, распределенные случайным образом.
Случайные величины характеризуются законами распределения. Часто на практике имеет место нормальный (гауссовский) закон распределения случайных величин. Кроме того, в том случае, если случайная погрешность является результатом совместного действия нескольких независимых случайных составляющих, каждая из которых вносит малую долю в общую погрешность, то, по какому бы закону ни были распределены эти составляющие, закон распределения результата их суммарного действия стремится к гауссовскому. Поэтому в методических указаниях МИ 1317-2004 определяется следующее: если имеются основания полагать, что реальная функция плотности распределения - функция симметричная, одномодальная, отличная от нуля на конечном интервале значения аргумента, и другая информация о плотности распределения отсутствует, то следует принимать закон, близкий к нормальному усеченному.
Методику обработки результатов наблюдений, полученных в процессе проведения измерений с многократными наблюдениями, определяет ГОСТ Р- 8736-2011 следующим образом.
В качестве значения результата измерений принимается оценка математического ожидания результатов наблюдений - их среднее арифметическое:

где
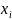 - значения наблюдений в выборке,
- значения наблюдений в выборке,
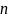 - количество наблюдений в выборке.
- количество наблюдений в выборке.
Иногда при вычислении среднего арифметического вручную удобно воспользоваться формулой:
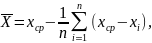
где
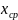 -вспомогательное
значение, выбранное в пределах диапазона
значений наблюдений в выборке.
-вспомогательное
значение, выбранное в пределах диапазона
значений наблюдений в выборке.
Результат измерений с многократными наблюдениями получают посредством обработки выборки наблюдений. При этом выборка может содержать значения, не соответствующие случайной величине. Такие значения называются промахами.
Промахи - грубые погрешности, обусловленные субъективными факторами (невнимательность оператора и др.) и не являющиеся объективной характеристикой измеряемой величины.
Грубая погрешность - погрешность измерения, существенно превышающая ожидаемую при данных условиях погрешность.
Для определения промахов используют
правило «трех сигм», так как при нормальном
законе распределения случайной величины
вероятность нахождения ее значений вне
интервала мала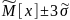 и составляет
и составляет
 .
Здесь
.
Здесь
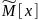 -
оценка математического ожидания
результатов наблюдений;
-
оценка математического ожидания
результатов наблюдений;
 - оценка среднего квадратичного отклонения
результатов наблюдений.
- оценка среднего квадратичного отклонения
результатов наблюдений.
Среднее квадратичное отклонение
результатов наблюдений - параметр
функции распределения результатов
наблюдений, характеризующий их рассеивание
и равный корню квадратному из дисперсии
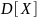 результатов наблюдения (с положительным
знаком):
результатов наблюдения (с положительным
знаком):
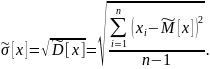
Чтобы определить примерный характер распределения необходимо первым делом построить гистограмму, где рациональное количество интервалов гистограммы можно оценить по формулам:
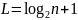 – критерий
Старджеса;
– критерий
Старджеса;
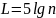 – критерий
Брукса и Каррузера;
– критерий
Брукса и Каррузера;
– критерий Хайнхольда и Гаеде.
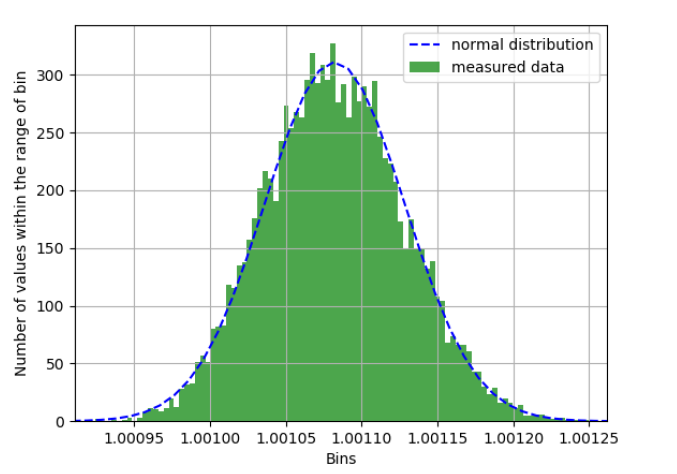
Рис.1. Гистограмма
Если результаты наблюдений можно считать принадлежащими нормальному закону распределения, то для обнаружения промахов в выборке используют правило «трех сигм», основанное на условном предположении, что все наблюдения выборки укладываются в интервал . Результаты наблюдений, которые выходят за пределы интервала , считают промахами и из выборки исключают.
Промахи из выборки исключают по одному, начиная с наиболее удаленного от оценки математического ожидания. При этом вновь вычисляются оценки математического ожидания и среднего квадратичного отклонения после исключения каждого промаха.
Приведенное выше правило исключения промахов, а также используемая в лабораторной работе методика вычисления результата измерений основаны на предположении, что случайная погрешность распределена по нормальному закону. Поэтому необходимо проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению.
Для проверки гипотезы ГОСТ Р 8736-2011
рекомендует использовать критерий
согласия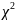 Пирсона, который основан на сравнении
двух гистограмм: практической из выборки
наблюдений и теоретической из
предположения, что наблюдения действительно
распределены по предполагаемому закону.
При этом необходимо наложить условия:
Пирсона, который основан на сравнении
двух гистограмм: практической из выборки
наблюдений и теоретической из
предположения, что наблюдения действительно
распределены по предполагаемому закону.
При этом необходимо наложить условия:
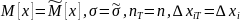 .
.
Теоретическая гистограмма формируется
из предположения, что моменты теоретического
распределения равны соответствующим
оценкам моментов практического
распределения
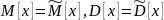 .
Интервалы целесообразно располагать
симметрично относительно математического
ожидания. При соблюдении данных условий
сравнение гистограмм можно свести к
сравнению практического
.
Интервалы целесообразно располагать
симметрично относительно математического
ожидания. При соблюдении данных условий
сравнение гистограмм можно свести к
сравнению практического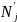 и теоретического
и теоретического количеств попаданий результатов
наблюдений в одноименные интервалы
гистограмм:
количеств попаданий результатов
наблюдений в одноименные интервалы
гистограмм:
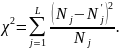
Практическое количество попаданий определяется непосредственным подсчетом соответствующих результатов наблюдений выборки. Теоретическое количество попаданий определяется следующим образом:
Рассчитывают ширину интервалов h по формуле:

где
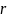 -
число интервалов, определенное по одному
из правил выше.
-
число интервалов, определенное по одному
из правил выше.
Далее вычисляют середины интервалов
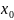 ,
среднее арифметическое -
,
среднее арифметическое -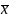 и
СКО - S.
и
СКО - S.
Для выбранного закона распределения вычисляют по формуле:
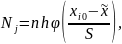
где
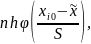 например,
плотность нормального распределения.
например,
плотность нормального распределения.
В
соответствии с критерием
Пирсона нет оснований отвергнуть
проверяемую гипотезу если выполняется
условие
 ,
где
,
где
 выбирается
равным 0,05 и 1-0,05 – вероятность отвергнуть
правильную гипотезу при условии принятия
решения отвергнуть проверяемую
гипотезу;
выбирается
равным 0,05 и 1-0,05 – вероятность отвергнуть
правильную гипотезу при условии принятия
решения отвергнуть проверяемую
гипотезу; -
число степеней свободы,
-
число степеней свободы,
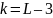 для нормального распределения.
для нормального распределения.
Случайная погрешность, приписываемая
значению результата измерений, может
быть представлена в виде доверительного
интервала, в котором с доверительной
вероятностью
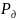 находится истинное значение измеряемой
величины.
находится истинное значение измеряемой
величины.
Доверительные границы погрешности результата измерений - верхняя и нижняя границы интервала, накрывающего с заданной вероятностью погрешность измерения.
Доверительные границы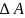 (без
учета знака) случайной составляющей
погрешности результата измерения
находят по формуле:
(без
учета знака) случайной составляющей
погрешности результата измерения
находят по формуле:
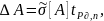
где
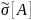 – оценка среднего квадратичного
отклонения результата измерения,
– оценка среднего квадратичного
отклонения результата измерения, –
коэффициент Стьюдента для доверительной
вероятности
и числа
результатов
наблюдений. Рекомендуемое значение
доверительной вероятности
–
коэффициент Стьюдента для доверительной
вероятности
и числа
результатов
наблюдений. Рекомендуемое значение
доверительной вероятности
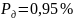 .
.
Оценка среднего квадратического отклонения результата измерения находится по формуле:
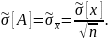
Если распределение нельзя признать нормальным, то точно функцию распределения установить не удается. В этом случае, опираясь на симметричность распределения можно рекомендовать следующую схему решения задачи.
В качестве числовой характеристики типа распределения экспериментальных данных принимаем значение κ, вычисляемое по формуле:

где S – выборочное СКО.
В зависимости от рассчитанного значения κ определяем формулу для оценки измеряемой величины:
κ< 2,5, тогда
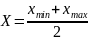 ;
;2,5 ≤ κ≤ 4, тогда
 ;
;κ> 4, тогда
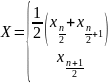 (первая
формула для четных n, вторая для нечетных).
(первая
формула для четных n, вторая для нечетных).
Результат измерения должен быть записан в соответствии с требованиями МИ 1317-86 с учетом количества значащих цифр, заслуживающих доверие:
результат измерений представляется именованным или неименованным числом;
совместно с результатом измерений должны быть представлены характеристики его погрешности;
характеристики погрешности измерений могут быть представлены в виде границ интервала, в пределах которого погрешность измерений находится с заданной вероятностью;
характеристики погрешности измерений, представленные в виде границ интервала, должны сопровождаться указанием вероятности, с которой они получены;
характеристики погрешности выражаются числом, содержащим не более двух значащих цифр;
наименьшие разряды числовых значений результатов измерений должны быть такими же, как наименьшие разряды характеристики погрешности;
представление результатов измерений, полученных как среднее арифметическое значение результатов многократных наблюдений, должно сопровождаться указанием числа наблюдений.
Определить в результате измерения количество значащих цифр n, заслуживающих доверие можно по следующим формулам:
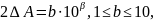

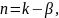
где –
это оценка истинного значения величины,
которая сначала представляется в виде
действительного числа от 1 до 10 кратное
10 в степени, а после разложенное в
многочлен по степеням 10.
–
это оценка истинного значения величины,
которая сначала представляется в виде
действительного числа от 1 до 10 кратное
10 в степени, а после разложенное в
многочлен по степеням 10.
