13. Разностные схемы решения дифференциальных уравнений в частных производных.
14. Классификация химических реакторов. Общая структура моделей химических реакторов.
КЛАССИФИКАЦИЯ ХИМИЧЕСКИХ РЕАКТОРОВ ПО НАЗНАЧЕНИЮ: химическим реактором называется система, предназначенная для преобразования вещества и энергии за счет протекающих в них химических реакций. Бывают: 1) Реакторы синтеза 2) Реакторы получения и преобразования энергии.
КЛАССИФИКАЦИЯ РЕАКТОРОВ ПО РЕЖИМУ ДВИЖЕНИЯ РЕАКЦИОННОЙ СРЕДЫ: 1) неподвижная 2) интенсивно перемешиваемая в замкнутом объеме 3) ламинарно-движущийся через реактор.
15. Математические модели теплообменных аппаратов.
16. Математические модели реакторов идеального смешения. (СМ ВОПРОС 15)
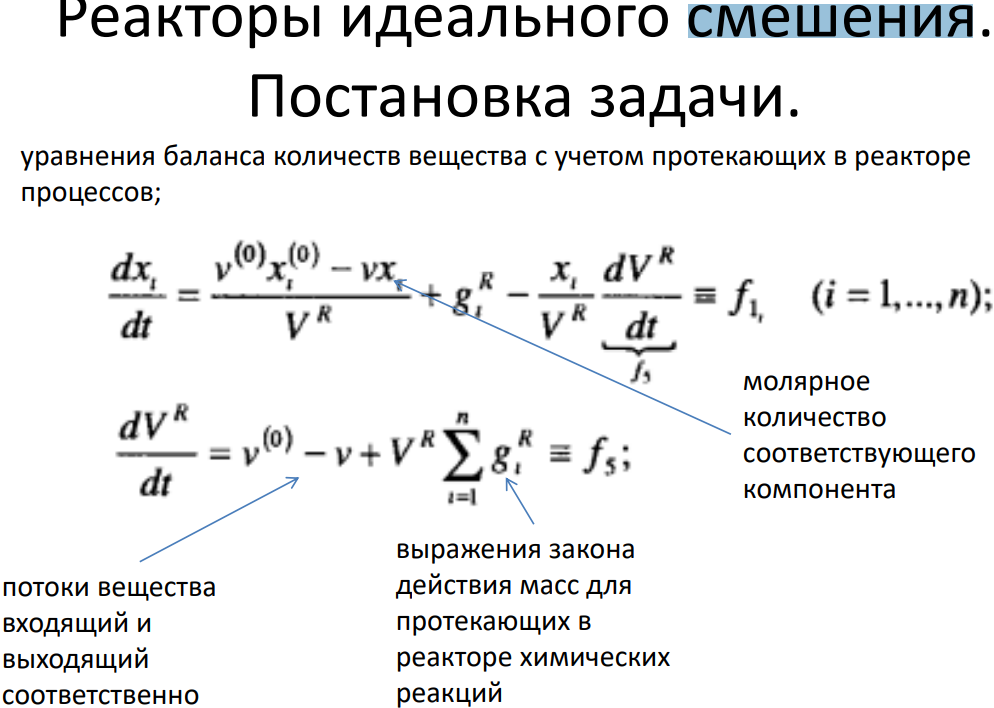
17. Математические модели реакторов идеального вытеснения.
или
18. Математические модели на основе экспериментальных данных. Задачи моделей.
Источники экспериментальных данных: 1) Реальный процесс 2) Физическая модель 3) Математическая модель.
Задачи математических моделей на основе экспериментальных данных:
1) Оценка функциональной связи
2) Вычисление функции в точках, в которых не проводился эксперимент
3) Вычисление производных таблично заданной функции
4) Вычисление интегралов таблично заданной функции
5) Нахождение экстремумов таблично заданной функции
6) Прогнозирование поведения функции, построенной на основе экспериментальных данных
7) Оценка констант теоретических моделей
19. Аппроксимация и интерполяция: определение, методы, оценки погрешностей.
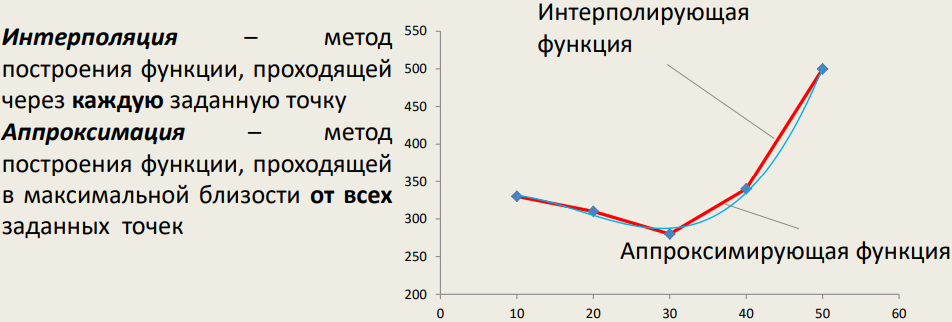
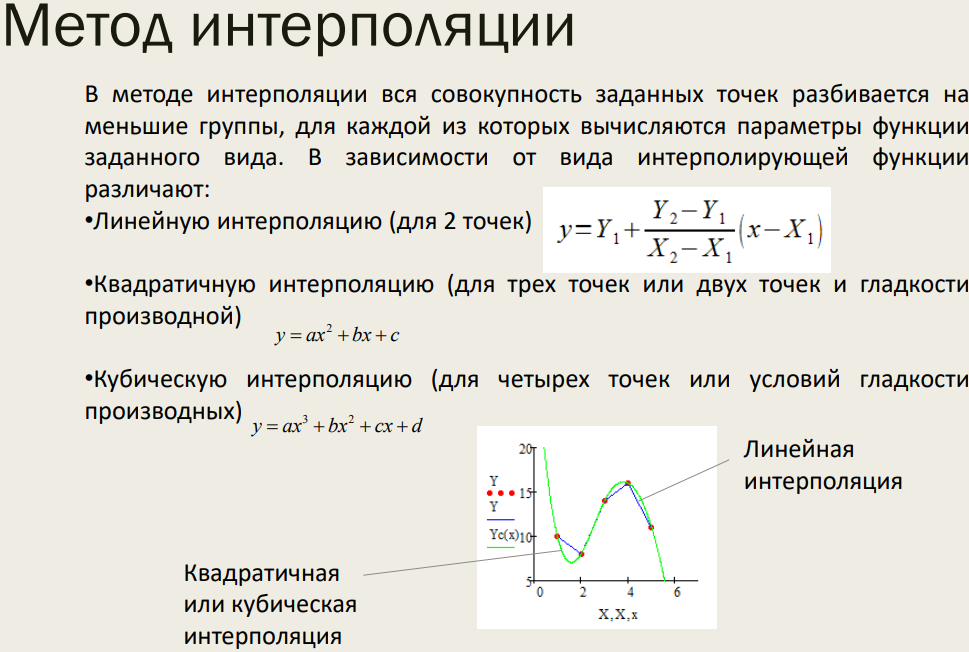
Интерполяция используется при построении гладких графиков по точкам, результат применяется для дифференцирования и интегрирования данных, но не слишком пригоден для прогнозов.
20. Коэффициент корреляции. Определение и области применения.
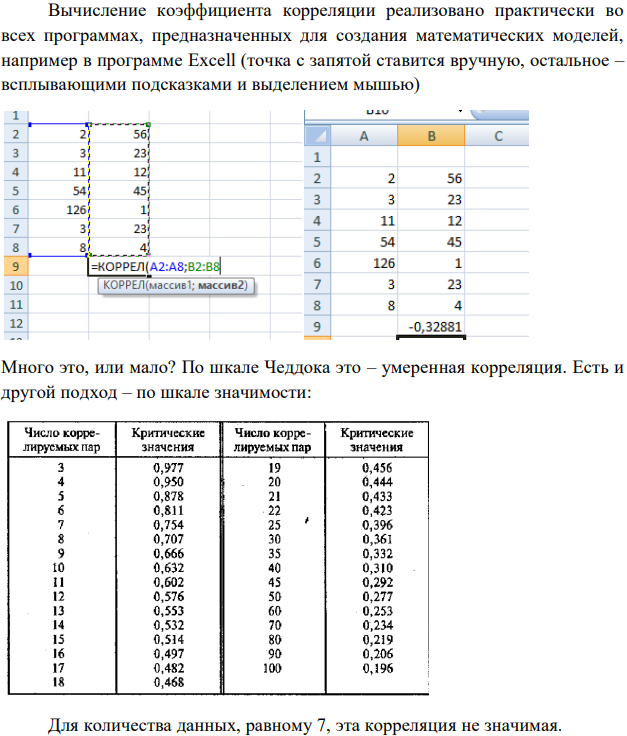
21. Нелинейная и множественная аппроксимация.
22. Оценка погрешностей аппроксимации.
Все экспериментальные данные содержат погрешности, которые выражаются в том, что если многократно повторять какое-либо измерение, результаты не будут совпадать в точности. Это связано с неизбежным влиянием на результат измерения множества малых по величине случайных факторов, которые в совокупности приводят к тому, что измеряемое значение, вообще говоря, является случайной величиной. Основными характеристиками случайных величин являются среднее значение, которое в пределе бесконечно большого числа измерений представляет собой математическое ожидание или значение, которое будет получено с наибольшей вероятностью.
23. Цели и задачи планирования эксперимента. Основные понятия: план эксперимента (матрица планирования), уравнение регрессии.
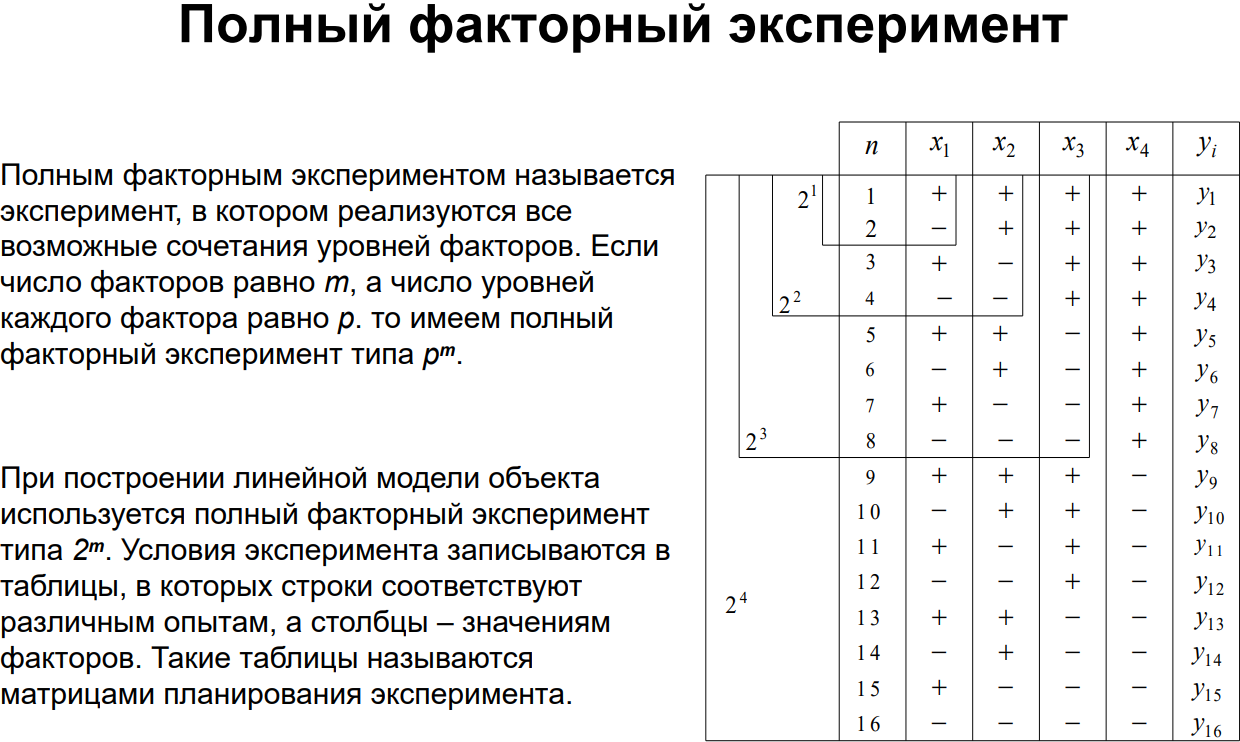
Условия эксперимента записываются в таблицы, в которых строки соответствуют различным опытам, а столбцы – значениям факторов. Такие таблицы называются МАТРИЦАМИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА.
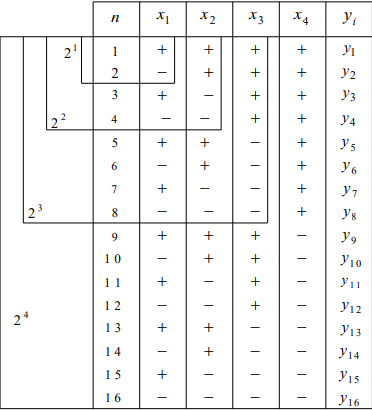
24. Планы полно-факторного эксперимента. Принципы построения.
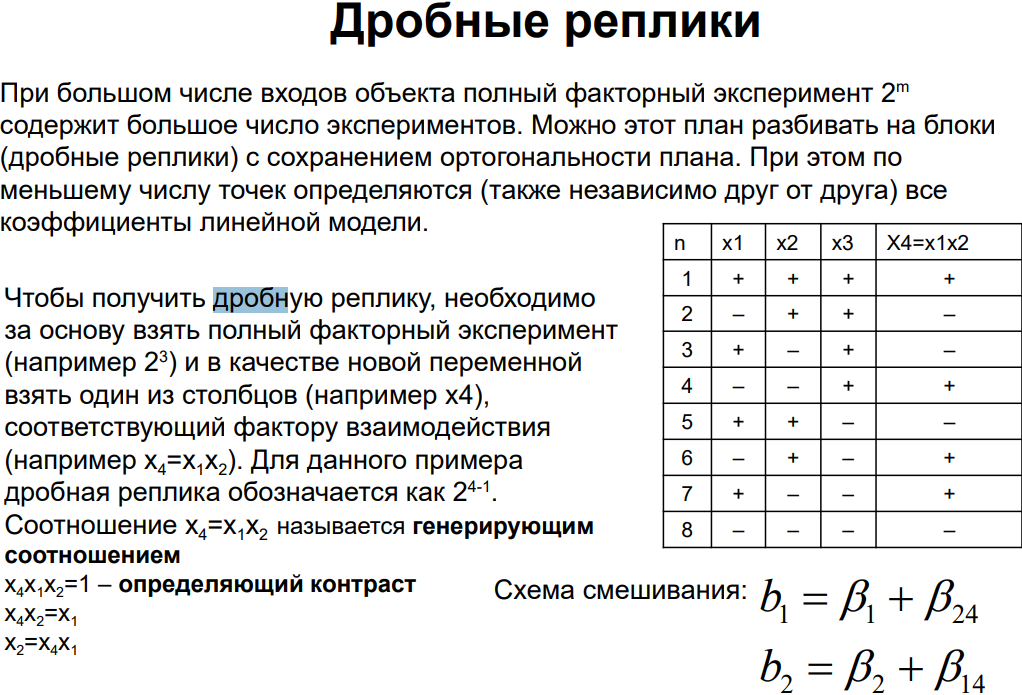
25. Дробный факторный эксперимент.
26. Крутое восхождение по поверхности отклика.
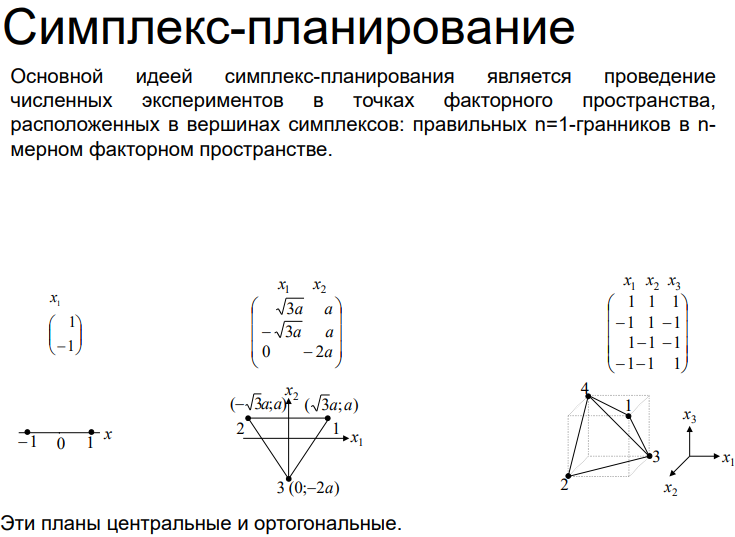
27. Симплекс-оптимизация.
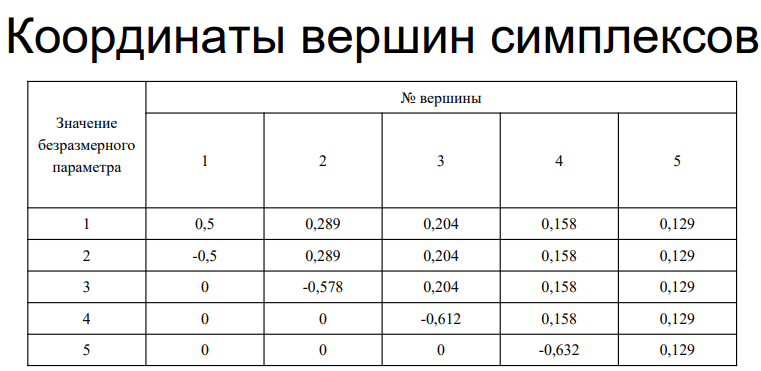
28. Получение и использование нелинейных уравнений регрессии. (тут тупо все с сдо)
https://sdo.srspu.ru/pluginfile.php/355901/mod_resource/content/1/lekziya%2015%20Polucheniye%20i%20ispolzovaniye%20nelineinjy%20regressii.pdf
