1. Цели и задачи математического моделирования.
Основная задача математического моделирования – выделение законов в природе, обществе и технике и запись их на языке математики.
Целью моделирования являются получение, обработка, представление и использование информации об объектах, которые взаимодействуют между собой и внешней средой; а модель здесь выступает как средство познания свойств и закономерности поведения объекта.
Математическая модель является приближенным представлением реальных объектов, процессов или систем, выраженным в математических терминах и сохраняющим существенные черты оригинала. Математические модели в количественной форме, с помощью логико-математических конструкций, описывают основные свойства объекта, процесса или системы, его параметры, внутренние и внешние связи.
2. Этапы создания математических моделей. Моделирование химико-технологических процессов состоит из нескольких этапов:
1. Идентификация объекта, т.е. разработка математического описания (образные модели).
2. Разработка алгоритма моделирования и выбор решения для данного математического описания.
3. Разработка программы расчёта и выполнение расчётов на ЭВМ.
4. Проверка адекватности (соответствия) математической модели на основании экспериментальных данных и адаптация модели к реальным условиям.
5. Интерпретация результатов расчётов и выдача рекомендаций по практической реализации исследуемого процесса.
3
.
Программные средства математического
моделирования.
4. Системы линейных алгебраических уравнений. Определение, методы решения, условия существования решений. Программная реализация решений СЛАУ.
Решить уравнение — это значит:
1) установить, имеет ли оно корни;
2) определить количество корней;
3) найти значение корней с заданной точностью.
Метод Гаусса (последовательное исключение переменных):
Другие методы:
5. Применение СЛАУ в решении задач составления уравнений материального баланса химико-технологического процесса.
6. Нелинейные алгебраические уравнения с одним неизвестным. Определение, методы решения: графические, численные.
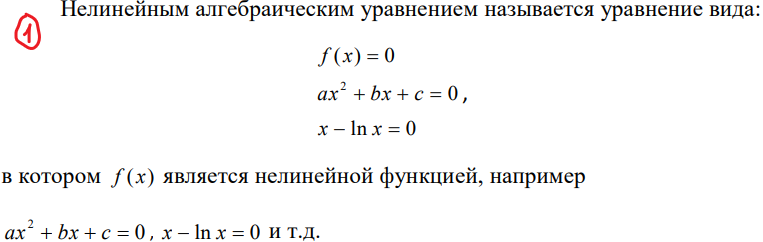
Решить уравнение — это значит:
1) Установить, имеет ли оно корни;
2) определить количество корней;
3) найти значение корней с заданной точностью.
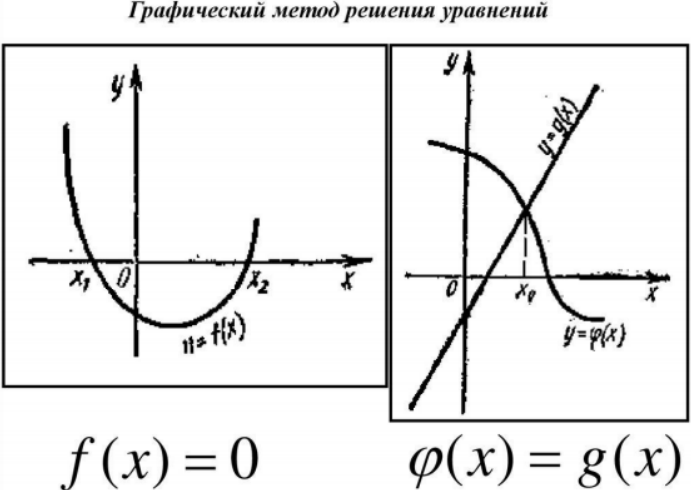
Графический метод основан на построении графика и нахождении координат точки пересечения графика с осью абсцисс или другим графиком:
Этот метод проще аналитического, но он по сути не решает двух первых вопросов решения, есть ли корни в принципе и сколько их. Кроме того, графический метод имеет ограниченную точность.
Численные методы:
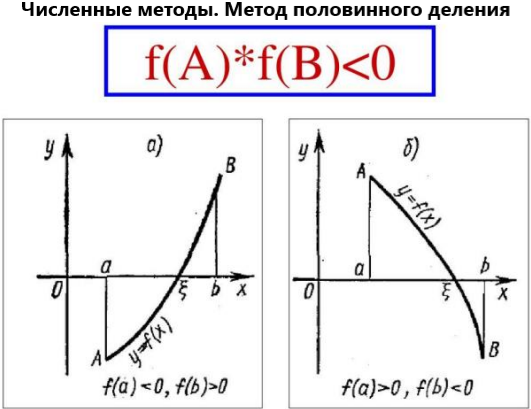
1 ) Метод половинного деления. В данном методе интервал делится ровно пополам. Такой подход обеспечивает гарантированную сходимость метода независимо от сложности функции. Недостатком метода является то, что сходимость метода всегда равна сходимости в наихудшем случае.
Т.е., метод половинного деления:
1. Один из простых способов поиска корней функции одного аргумента.
2. Применяется для нахождения значений действительно-значной функции, определяемому по какому-либо критерию (это может быть сравнение на минимум, максимум или конкретное число).
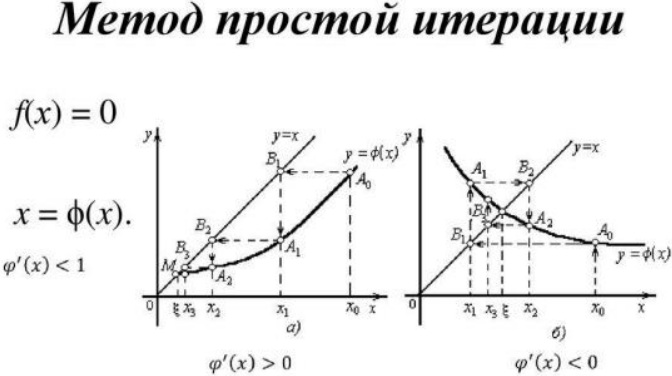
2) Метод касательных — численный метод нахождения (одного) решения (с заданной точностью ε) нелинейного уравнения вида f(x)=0.
