7. Программная реализация численных методов решения нелинейных алгебраических уравнений.
8 . Программная реализация решения систем нелинейных алгебраических уравнений. Расчет химических равновесий.
Основным методом решения систем нелинейных алгебраических уравнений являются численные методы, а именно – метод итераций, который реализован в блоке Find программы MathCad. Этот блок оформляется следующим образом: (слева)
Первая строка записи – это задание начального приближения итерационного процесса, вторая обозначает начало записи решаемых уравнений, последняя является командой выполнения алгоритма, в результате которого после знака равенства (без двоеточия) выводится результат расчета.
Химические равновесия являются широко применяемыми математическими моделями химико-технологических систем, которые позволяют рассчитать выход продукта, концентрации всех участников реакции в зависимости от требуемых исходных данных.
Вид моделей хмического равновесия – выражение константы химического равновесия, например для одной реакции:
в которой строчными буквами обозначены стехиометрические коэффициенты. Константа равновесия имеет вид:
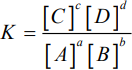
Одно только выражение константы химического равновесия – это одно уравнение с количеством переменных более одного, поэтому оно имеет бесконечное множество решений. Чтобы решение существовало, выражение константы равновесия необходимо дополнить начальными условиями и уравнениями баланса вещества и электрического заряда (если реакция происходит по ионному пути).
Расчет химических равновесий:
9. Обыкновенные дифференциальные уравнения (ОДУ). Определение, общие и частное решение, методы решения.
Методы решения:
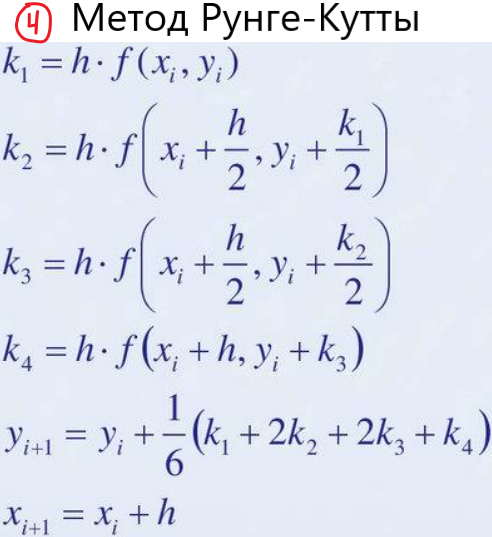
10. Программная реализация решений ОДУ.
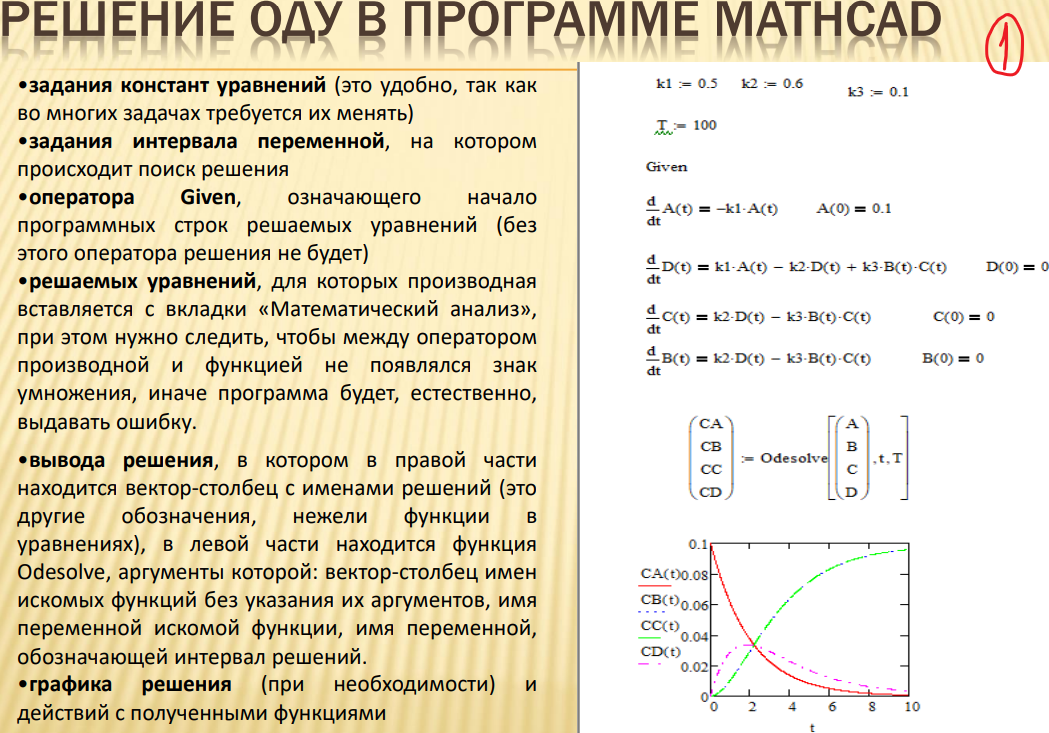
11. Моделирование кинетических схем химических реакций.
12. Дифференциальные уравнения в частных производных, классификация, методы решения.
Методы решения:
Методы решения ЛДУ делятся на аналитические, приближенные и численные.
Приближенные методы решения ОДУ можно разделить на два больших класса: аналитические и численные. Существуют и другие классы приближенных методов для решения ОДУ, например, аналитико-численные или косвенно-численные, графические и др.
Аналитические методы основаны на тождественных преобразованиях исходного ЛДУ, позволяющих получить решение в виде элементарных или специальных функций, например решение уравнения диффузии на полубесконечном интервале с начальным условием:
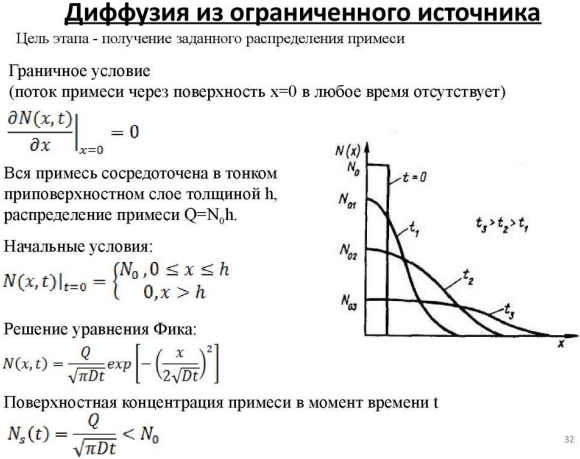
Численные методы позволяют свести решение задачи к выполнению конечного количества арифметических действий над числами, при этом результаты получаются в виде числовых значений.