Лаб по С и С++ / Лаб_С_№3

ЗАДАЧИ ПО ТЕМЕ “Ветвление и функции, возвращающие 1 результат ”

Условия выбора варианта

подгруппа	1	2	3
№ машины	№ варианта	№ варианта	№ варианта
1	10	5	1
2	9	6	2
3	8	7	3
4	7	8	4
5	6	9	5
6	5	10	6
7	4	1	7
8	3	2	8
9- admin	2	3	9
10**	1	4	10

Необходимо написать функции, решающие поставленную задачу.

1. 1. 

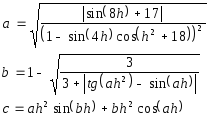
      Даны действительные числа x и у. Получить: max(x,y) и min(x,y);

   2. Дано действительное число h. Выяснить, имеет ли уравнение ax²+bx+c=0 действительные корни, если

Если действительные корни существуют, то найти их. В противном случае ответом является сообщение, что действительных корней нет.

2. 1. Даны действительные числа x, y и z . Получить: max(x,y,z); min(x,y,z);

   2. Даны действительные числа a₁,b₁,c₁ ,a₂,b₂,c₂ . Выяснить, верно ли, 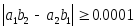, и если верно, то найти решение системы линейных уравнений

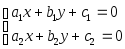
3. 1. Даны действительные числа x, y и z . Получить: max(x+y+z,xyz); min²(x+y+z,xyz)+1

   2. Даны действительные положительные числа a, b, c, d. Выяснить можно ли прямоугольник со сторонами a, b, уместить внутри прямоугольника со сторонами c, d так, чтобы каждая из сторон одного прямоугольника была параллельна или перпендикулярна каждой стороне второго прямоугольника.

4. 1. Даны действительные числа a, b и c . Проверить выполняется ли неравенство: a<b<c.

   2. Даны действительные положительные числа a, b, c, x, y. Выяснить пройдёт ли кирпич с рёбрами a, b, c в прямоугольное отверстие со сторонами x, y . Просовывать кирпич в отверстие разрешается только так, чтобы каждое из его рёбер было параллельно или перпендикулярно каждой из сторон отверстия.

5. 1. Даны действительные числа a, b и c . двоить эти числа, если abc, и заменить их абсолютными значениями, если это не так

   2. Даны действительные положительные числа a, b, c, d. Выяснить можно ли прямоугольник со сторонами a, b, уместить внутри прямоугольника со сторонами c, d так, чтобы каждая из сторон одного прямоугольника была параллельна или перпендикулярна каждой стороне второго прямоугольника.

6. 1. Даны действительные числа x и у. Вычислить z:

1. Даны действительные числа x₁,x₂,x₂ ,y₁,y₂,y₃ . Принадлежит ли начало координат треугольнику с вершинами(x₁, y₁),(x₂,y₂),(x₂ , y₃).

1. 1. Даны два действительных числа. Вывести первое число, если оно больше второго, и оба числа, если это не так

   2. Дано действительное число а. Вычислить 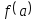, если

8. 1. Даны два действительных числа. Заменить первое число нулём, если оно меньше или равно второму, и оставить числа без изменения в противном случае.

   2. Дано действительное число а. Вычислить 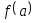, если

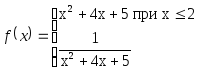
9. 1. Даны три действительных числа. Выбрать из них те, которые принадлежат интервалу (1,3).

   2. Дано действительное число а. Вычислить 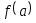, если

10. 1. Даны действительные числа x и у (xy). Меньшее из этих чисел заменить их полусуммой, а большее — их удвоенным произведением

    2. Дано действительное число а. Вычислить 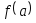, если