
Лаб по С и С++ / Лаб_С_№4
.docЗАДАЧИ ПО ТЕМЕ “ФУНКЦИИ И ЦИКЛЫ”
Условия выбора варианта
|
подгруппа |
1 |
2 |
3 |
|
№ машины |
№ варианта |
№ варианта |
№ варианта |
|
1 |
1 |
11 |
21 |
|
2 |
2 |
12 |
22 |
|
3 |
3 |
13 |
23 |
|
4 |
4 |
14 |
24 |
|
5 |
5 |
15 |
25 |
|
6 |
6 |
16 |
26 |
|
7 |
7 |
17 |
27 |
|
8 |
8 |
18 |
28 |
|
9- admin |
9 |
19 |
29 |
|
10** |
10 |
20 |
30 |
-
-
Дано натуральное число n. Вычислить:
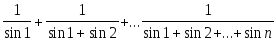
-
Пусть u1=u2=0;v1=v2=1; i=1,2,...
-
![]()
Дано натуральное n (n3). Получить vn.
-
-
Дано натуральное число n. Вычислить:
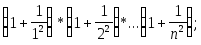
-
Пусть a1=b2=1
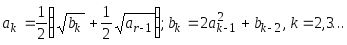 Дано натуральное n.
Найти
Дано натуральное n.
Найти
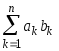 .
.
-
-
-
Даны действительные х, натуральное n. Вычислить
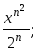
-
Пусть
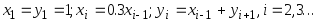 Дано натуральное n.
Найти
Дано натуральное n.
Найти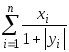 .
.
-
-
-
Даны действительные х, натуральное n. Вычислить
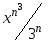
-
Пусть
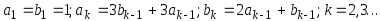 Дано натуральное n.
Найти
Дано натуральное n.
Найти
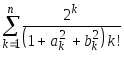 .
.
-
-
-
Дано натуральное число n. Вычислить
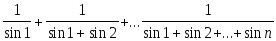 :
:
-
Пусть
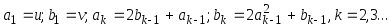 .
Даны действительные u,
v,
натуральное n.
Найти
.
Даны действительные u,
v,
натуральное n.
Найти
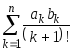 .
.
-
-
-
Дано натуральное число n. Вычислить:
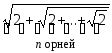
-
Пусть
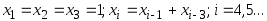 .
Найти
.
Найти
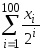 .
.
-
-
-
Дано натуральное число n. Вычислить:
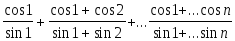
-
Даны действительные положительные a,x,. В последовательности y1,y2,...yn , образованной по закону
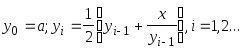 найти первый член yn
для которого выполняется неравенство
найти первый член yn
для которого выполняется неравенство
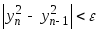 .
.
-
-
-
Дано натуральное число n. Вычислить:
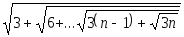
-
Пусть
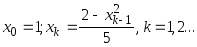 .
найти первый член xn
для которого выполняется неравенство
.
найти первый член xn
для которого выполняется неравенство
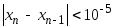 .
.
-
-
-
даны действительное число а, натуральное число n. Вычислить:
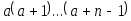
-
Пусть
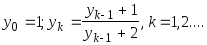 .
найти первый член yn
для которого выполняется неравенство
.
найти первый член yn
для которого выполняется неравенство
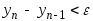 .
.
-
-
-
даны действительное число а, натуральное число n. Вычислить:
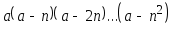
-
Дано действительное положительное a. Последовательность х0, х1, ... образована по закону
-

![]() найти первый член
xn
для которого выполняется неравенство
найти первый член
xn
для которого выполняется неравенство
![]() .
Вычислить для найденного значения
разность
.
Вычислить для найденного значения
разность
-
-
даны действительное число а, натуральное число n. Вычислить:
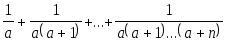
-
Вычислить
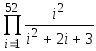 ;
;
-
-
-
даны действительное число а, натуральное число n. Вычислить:
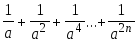
-
Алгоритм Евклида нахождения наибольшего общего делителя (НОД) неотрицательных целых чисел основан на следующих свойствах этой величины. Пусть m и n — одновременно не равные 0 целые неотрицательные числа и пусть mn. Тогда, если n=0, то НОД(m,n)=m, а если n0, то для m, n и r, где r—остаток от деления m на n, выполняется равенство НОД(m,n)=НОД(n,r). Например НОД(15,6)= НОД(6,3)= НОД(3,0)=3. Даны натуральные числа n и m. Используя алгоритм Евклида, найти НОД(m,b).
-
-
-
даны действительное число а, натуральное число n. Вычислить:
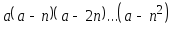
-
Даны натуральные числа n и m. Найти такие натуральные p и q, не имеющие общих делителей, что m/n=p/q.
-
-
-
вычислить (1+sin0.1*(1+sin0.2)*...*(1+sin10).
-
Пусть v1=v2=0, v3=1.5;
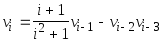 ,
i=4,5
Дано натуральное n>4
Получить vn.
,
i=4,5
Дано натуральное n>4
Получить vn.
-
-
-
Дано действительное число х. Вычислить:
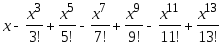
-
Дано натуральное число n. Сколько цифр в числе n? Чему равно сумма его цифр?
-
-
-
Дано действительное число х. Вычислить
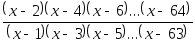
-
Даны действительные a, b, (b>a), натуральное n. Получить
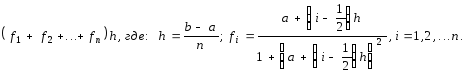
-
-
-
Дано целое число m>1. Получить наибольшее целое k, при котором 4k>m.
-
Вычислить
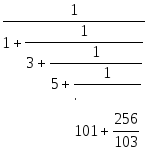
-
-
-
Дано целое число n. Получить наименьшее число вида 2r , превосходящее n.
-
Даны действительные х0, вычислить:
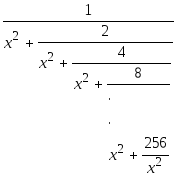
-
-
-
Даны целые числа n, k (nk0). Вычислить
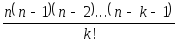
-
Вычислить
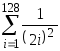 ;
;
-
-
-
Вычислить
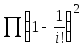 ;
; -
Пусть n— натуральное число и n!! Обозначает 1*3*5...*т для нечётного n и 2*4*6...*n для чётного n. Для заданного натурального n вычислить
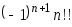
-
-
-
Даны действительные числа x, a ,натуральное n. Выполнить:
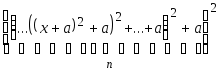
-
Пусть а0=1; ak=kak-1+1/k; k=1,2,... Получить an.
-
-
-
Даны натуральное n, действительное х. Вычислить
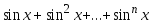
-
Пусть v1=v2=0, v3=1.5;
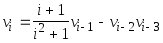 ,
i=4,5
Дано натуральное n>4
Получить vn
,
i=4,5
Дано натуральное n>4
Получить vn
-
-
-
Даны натуральное n, действительное х. Вычислить
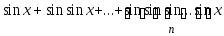
-
Пусть х0=с,х1=d; xk=qxk-1+rxk-2+b; k=2,3,... Даны действительные q, r, b, c, d, натуральное n>2. Получить хn.
-
-
-
Дано действительное число а. Найти среди чисел 1,1+1/2,1+1/2+1/3+... первое, большее а
-
Даны действительные a, b, (b>a), натуральное n. Получить :
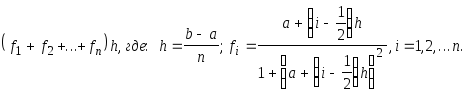
-
-
-
Дано действительное число а. Найти такое наименьшее n , что 1+1/2+1/3+...+1/n > а.
-
Даны целые числа n, k (nk0). Вычислить
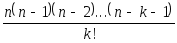
-
-
-
Найти знакочередующуюся сумму цифр числа n ( пусть запись n в десятичной системе есть kk-1...0; найти л-л-1+...(-1)k0).
-
Пусть n— натуральное число, вычислить
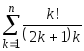 ;
;
-
-
-
Даны натуральные числа n, m. Получить сумму m последних цифр числа n.
-
Пусть n— натуральное число, вычислить
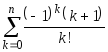
-
-
-
Даны действительные числа a, h, натуральное n. Вычислить
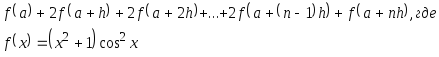
-
Найти знакочередующуюся сумму цифр числа n ( пусть запись n в десятичной системе есть kk-1...0; найти л-л-1+...(-1)k0).
-
-
-
Дано натуральное число n. Вычислить:
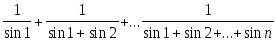
-
Пусть u1=u2=0;v1=v2=1; i=1,2,...
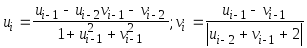 Дано
натуральное n
(n3).
Получить vn.
Дано
натуральное n
(n3).
Получить vn.
-
-
-
Дано натуральное число n. Вычислить:
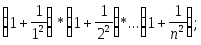
-
Пусть a1=b2=1 ;
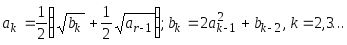 Дано натуральное n.
Найти
Дано натуральное n.
Найти
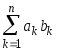 .
. -
Пусть
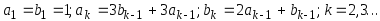 Дано натуральное n.
Найти
Дано натуральное n.
Найти
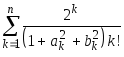 .
.
-
