2413

источник света и точка наблюдения удалены от препятствия, вызвавшего дифракцию, на бесконечно большое расстояние.

Параллельные лучи света формирует точечный источник света, помещаемый в фокусе собирающей линзы. Дифракцию наблюдают в фокальной плоскости другой линзы, установленной за препятствием.

Пусть плоская монохроматическая волна падает нормально к плоскости узкой бесконечно длинной щели шириной а (рис.56, а). Оптическая разность хода между крайними лучами МС и ND, распространяющимися от щели в произвольном направлении определяемом углом , равна

NF asin .

Рис.56

Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна / 2 . При таких условиях число зон умещающихся на ширине щели равно NФ / ( / 2) .

Световые лучи падают на щель нормально. Плоскость щели совпадает с волновым фронтом. Поэтому фазы колебаний всех точек волнового фронта в плоскости щели будут одинаковые.

91

Амплитудывторичныхволнвплоскостищелибудутравны. Этосвязано с тем, что выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к плоскости наблюдения.

Число зон Френеля NФ , укладывающихся на открытой части волнового

фронта, зависит от угла . Это число определяет характер дифракционной картины на экране формируемый результатами наложения всех вторичных волн.

Дифракция Фраунгофера на щели (2) (условия максимумов и минимумов)

Если число зон Френеля четное, то

asin 2 2 (m = 1, 2, 3, ...),

и на экране в точке В наблюдается дифракционный минимум (колебания от каждой пары соседних зон взаимно гасят друг друга).

Если число зон Френеля нечетное, то

asin (2m 1) 2 (m = 1, 2, 3, ...)

и при таком условии наблюдается дифракционный максимум (одна зова Френеля не скомпенсирована).

В направлении, определяемом углом равном 0 , щель действует как

одна зона Френеля. В этом направлении свет распространяется с наибольшей интенсивностью и в точке В наблюдается центральный дифракционный максимум.

Направления на точки экрана, в которых амплитуда (и интенсивность) максимальна и минимальна описываются соотношениями

sin max (2m 1) 2a и sin min m 2a .

Распределениеинтенсивности света по длинеэкрана, получаемоевследствие дифракции, называется дифракционным спектром. Из рисунка видно, что отношения интенсивностей света в центральном и последующих дифрак-

I3 / I0 0,83 10 2 …. Поэтому основная часть световой энергии сосредо-

точена в центральном максимуме.

При уменьшении размера щели (a ) центральный максимум расплывается (его интенсивность уменьшается), а при расширении (a ) –

дифракционныеполосыуменьшаютсяпоразмерам, акартинаосвещённости на экране становится более яркой.

При a в центре дифракционной картины получается резкое изображение источника света. Этот факт подтверждает, что свет через щель распространяется прямолинейно.

92

Положение максимумов интенсивности света на экране зависит от длины волны . Поэтому при освещении щели белым светом центральный максимум имеет вид белой полоски общей для всех длин волн (при 0

разность хода равна нулю для всех ). Боковые максимумы радужно окрашены, так как условие максимума при различных m различны.

С помощью дифракции на одной щели получить отчетливое пространственное разделение на экране различных длин волн 1 и 2 невозможно.

Это связано с расплыванием дифракционных максимумов.

Дифракция Фраунгофета на дифракционной решетке

Дифракционнаярешетка– этоустройство, состоящееизсовокупности параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.

Дифракционнаякартинанаэкранеопределяетсякакрезультатвзаимной интерференции волн, идущих от всех щелей. Другими словами, в дифракционной решетке осуществляется многолучевая интерференция когерентных дифрагированных пучков света, идущих от всех щелей.

Пространственный период дифракционной решетки равен

Условия для наблюдения главных максимумов, главных минимумов и дополнительных минимумов в случае дифракционной решетки записываются в виде соотношений:

m = 1, 2, 3, …;

0, N, 2N…, N – число штрихов решётки.

При наличии в решётке N щелей между двумя главными максимумами на экране располагаются N – 1 дополнительных минимумов, разделенных N – 2 вторичнымимаксимумами, создающимивесьмаслабыйфоннаэкране.

Число максимумов, формируемых дифракционной решеткой с

учётом неравенства sin 1 равно m d .

Дифракционная решётка выполняет функцию разложения белого света в спектр и может использоваться в качестве спектрального прибора.

Спектр светового излучения представляет собой непрерывный или дискретный набор длин (частот) электромагнитных волн от min до max

( min до max ).

93

Дифракция на пространственной решетке

Пространственные (трехмерные) решетки представляет собой про-

странственные образования, в которых элементы структуры подобны по форме, имеют геометрически правильное и периодически повторяющееся расположение, а также постоянные (пространственные периоды) решеток d , соизмеримые с длиной волны электромагнитного излучения .

В качестве пространственных дифракционных решеток используют кристаллические тела. Неоднородности (атомы, молекулы, ионы) в них регулярноповторяютсявтрехнаправленияхдекартовойсистемыкоординат

i , j и k .

Для наблюдения дифракции необходимо, чтобы постоянная решётки была соизмерима с длиной волны d . Поэтому кристаллические вещества могут использоваться для изучения дифракции рентгеновского излучения, характеризуемого малой длиной волны рент по сравнению с

длиной волны оптического (видимого светового) излучения опт

рент опт, рент опт .

Соотношение Вульфа – Брэггов получено при рассмотрении пучка параллельных монохроматических рентгеновских лучей (1, 2) падающих (рис.57) под углами скольжения ϑ (угол между направлением падающих лучей и кристаллографической плоскостью).

Данный пучок возбуждает атомы кристаллической решетки и они становятся источниками когерентных вторичных волн 1 и 2 , интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки. Максимумы интенсивности (дифракционные максимумы) на-

Рис.57 блюдаются в направлениях, в которых все отраженныеатомными плоскостями волны будут находиться в одинаковой фазе. Такие направ-

ления описывает соотношение Вульфа – Брэггов d sin m ,

где т=1, 2, 3, ...

Оно указывает, что при разности хода d sin между двумя лучами рентгена отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн , наблюдается дифракционный максимум.

Соотношение Вульфа – Брэггов даёт возможность оценивать неизвестные параметры излучений при наличии известных

94

Рентгеноструктурный анализ предусматривает измерение и m и по известной длине волны оценивать пространственный период кристаллического вещества d.

Измерения параметров и m в методе рентгеновской спектроскопии дают возможность при известном параметре d найти длину волны .

Критерий Рэлея.

Разрешающая способность спектрального прибора

Критерий Рэлея указывает, что даже при существовании идеальной оптической системы (дефектов и аберраций нет), изображение любой светящейся точки на экране из-за волновой природы света будет в виде центрального светлого пятна, окруженного чередующимися темными и светлыми кольцами.

Согласно критерию Рэлея, изображения двух близлежащих одинаковых точечных источников или двух близлежащих спектральных линий

сравными интенсивностями и одинаковыми симметричными контурами (рис.59) разрешимы (разделены для восприятия), если центральный максимум дифракционной картины от одного источника (линии) совпадает

спервым минимумом дифракционной картины от другого (рис. 59, а).

При выполнении критерия Рэлея

интенсивность “провала” между максимумами составляет 80% интенсивности в максимуме, что является достаточным для разрешения линий 1 и 2 на экране.

Если критерий Рэлея нарушен, то наблюдается одна линия (рис. 58, б).

Разрешающая способность спектрального прибора – это безразмерная величина, определяемая уравнением

R / ,

где – абсолютное значение минимальной разности длин волн двух соседних спектральных линий, при которой эти линии регистрируются на экране раздельно.

Разрешающую способность дифракционной решетки Rдиф.реш оцени-

вают с учётом дифракционного максимума m-го порядка для 2 , наблю-

даемого под углом и описываемого соотношением d sin m .

При переходе от максимума к соседнему минимуму разность хода меняется на / N , где N – число щелей решетки. Следовательно, минимум1 , наблюдаемый под углом min , удовлетворяет условию

95

от друга 2 1 очень малая величина, то разрешающая способность

дифракционной решетки определяется из уравнения

Rдиф.реш mN .

Контрольные вопросы

1.Перечислите дополнения, которыевнёсФренель впринципГюйгенса?

2.В чем состоит принцип построения зон Френеля?

3.По какому принципу действуют зонные пластинки?

4.При каких условиях наблюдается дифракция Френеля и Фраунгофера?

5.Почемудифракцияненаблюдаетсянабольшихотверстияхибольших дисках? Что означают термины «больший» и «меньший»?

6.Как влияет на дифракцию Фраунгофера от одной щели увеличение длины волны и ширины щели?

7.Какопределяютнаибольшийпорядокспектрадифракционнойрешетки?

8.Как изменится дифракционная картина при удалении экрана от решетки?

9.Почему при использовании белого света только лишь центральный максимум белый, а боковые максимумы радужно окрашены?

10.Почему штрихи на дифракционной решетке должны быть тесно расположены друг к другу? Почему их должно быть большое число?

11.Запишите условия дифракционных минимумов для одной щели и главных максимумов для решетки. Каков характер этих дифракционных картин?

12.Почему на кристаллах не наблюдается дифракция видимого света и наблюдается дифракция рентгеновского излучения?

13.Каков механизм рассеяния света в мутной среде и в чистой среде?

14.Как объяснить голубой цвет неба? Почему при закате и восходе солнце кажется красным?

15.Какие практические применения имеет формула Вульфа – Брэггов?

16.Когда два одинаковых точечных источника света разрешимы по Рэлею?

17.От чего зависит разрешающая способность дифракционной решетки

икак получить уравнение для её определения?

18.Почему для получения голограммы, кроме предметной волны необходима еще и опорная волна?

19.В чем заключается идея голографирования?

96

2.4. Взаимодействие электромагнитных волн с веществом

Дисперсия света

Дисперсия света определяется зависимостями абсолютного показателя преломлениявещества n отчастоты падающегонавеществосветаилиот длины световой волны в вакууме 0 или в какой-либо среде:

n ( 0 ) и n ( ) ,

где 0 с и – длины волн в вакууме и среде.

Абсолютноый показатель преломления вещества n оценивается с учётом фазовой скорости света в среде из уравнения n с . Скорость

света длина волны и частота связаны друг с другом соотношением . Поэтому дисперсия света определяется также и зависимостью фазовой

скорости света в среде от его частоты n с с .

Разложение в спектр пучка белого света при прохождении его сквозь оптически прозрачное вещество в форме призмы просходит вследствие явления дисперсии.

Дисперсиясветавозникаеттольколишьприраспространениинемонохроматических волн. Немонохроматическим волнами являются волны, состоящие из непрерывного набора длин электромагнитных волн или полосы частот

max min , max min ,

где max , min ( max , min ) – максимальные и минимальные длины волны

(частоты волн).

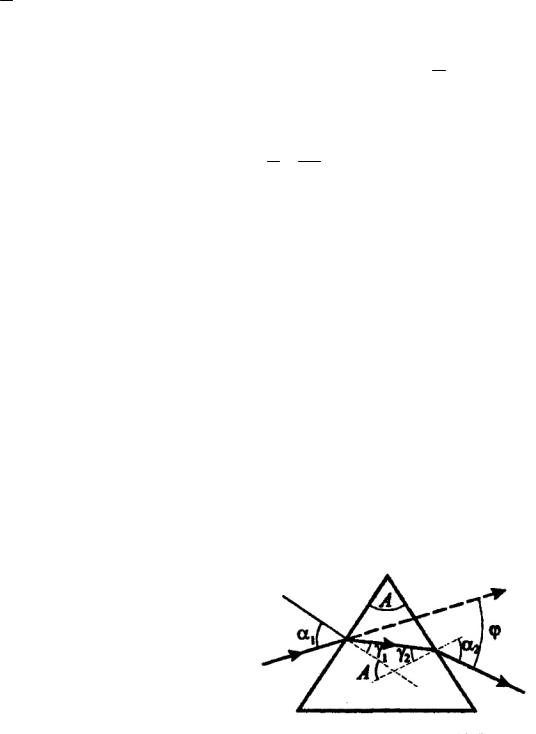
Определение угла отклонения монохроматического луча света призмой проводят путём анализа хода в ней лучей (рис.59).

Если монохроматический луч света падает на призму с показателем преломления n под углом 1 , а преломляющий угол равен A, то после

двукратного преломления (на левой и правой гранях призмы) луч света оказывается отклоненным на угол . Из рисунка следует; что угол равен

( 1 1) ( 2 2 ) 1 2 А.

Если углы A н 1 , малы, то утлы

2 , 1 и 2 также малы и вместо

синусов этих углов используемых по законам преломления можно воспользоваться их значениями. Осюда

( 1 / 1) n и ( 2 / 2 ) 1. Так как

1 2 ,

97 Рис.59

то 2 2n n( A 1) n( А 1 / n) nA 1 или 1 2 nA.

Отсюда преомляющий угол призмы определяется из уравнения

А(n 1) .

Различия в дифрационом и призматическом спектрах. Нормальная и аномальная дисперсия

Спектральный состав света изучают на практике с помощью призменных и дифракционных спектрографов. Данные приборы позволяют экспериментально изучать характер светового излучения и поглощения света с целью определения непрерывного ( min max ) или дискретного

набора длин электромагнитных волн ( 1, 2 , 3.... N ).

Призмы и дифракционные решётки по разному осуществляют разложение светового излучения по длинам волн .

Различия в дифракционном и призматическом спектрах:

1. Дифракционнаярешеткаразлагаетпадающийсветнепосредственно по длинам волн по закону d sin m и по измеренным углам дифрагиро-

ванных лучей (направления соответствующих максимумов) позволяет вычислить длину волны .

Призмавотличиеотдифракционнойрешеткиразлагаетсветвспектр

сучётом характера изменения показателя преломления n от длины волны

. Поэтому для измерения длины волны лучей от источников света, необходимо иметь информацию о зависимости показателя преломления призмы спектрографа от длины волны n f ( ) (рис.60).

2.Составные цвета в дифракционном и призматическом спектрах располагаются по шкале длин волны различно.

Из соотношения для дифракци-

онной решётки d sin m видно,

что синус угла отклонения лучей света пропорционален длине волны

sin d1 m . Следовательно, красные лучи, имеющие большую длину

Рис.60

волны, чем фиолетовые кр ф ,

отклоняются дифракционной решеткой сильнее кр ф.

Призма в отличие дифракционной решетки также разлагает лучи в спектр. Однако, её действие зависит от значений показателя преломления n f ( ) , который для всех прозрачных к свету веществ с увеличением

98

длиныволныуменьшается(см. рис.61). Поэтомукрасныелучиотклоняются призмой слабее, чем фиолетовые.

Дисперсия вещества D – это величина, которая определяется первой производной от показателя преломления n f ( ) по длине волны

D ddn .

Дисперсия вещества является мерой скорости изменения показателя преломления от длины волны .

Дисперсия вещества считается нормальной, если с уменьшением длины волны величина D ddn увеличивается.

Вывод о существовании нормальной дисперсии следует из анализа кривой линии n f ( ) изображённой на рис. 61. Видно, что показатель

преломления n для прозрачных веществ с уменьшением длины волны увеличивается, следовательно, величина D ddn , определяемая из графика

n f ( ) тангенсом угла наклонакасательной tg n , при уменьшении

также увеличивается.

Дисперсия вещества считается аномальной, если показатель преломления n с уменьшением длины волны уменьшается.

Ниже будет показано, что такой ход кривой дисперсии n f ( )

наблюдается вблизи линий и полос поглощения света некоторыми веществами. Показатель преломления п у таких веществ с уменьшением длины волны уменьшается.

Элементарная электронная теория дисперсии веществ обоснована теорией Максвелла. По Максвеллу абсолютный показатель преломления среды определяется из уравнения

n ,

где и – диэлектрическая и магнитная проницаемости вещества.

В оптической области спектра магнитная проницаемость для всех веществ 1 и абсолютный показатель преломления вещества (среды)

является переменной величиной, зависящей от диэлектрической проницаемости вещества (среды) :

n .

Согласно электронной теории, дисперсия света возникает вследствии зависимости от частоты световых волн f ( ) .

Диэлектрическая проницаемость вещества описывается уравнением

1 1 P / 0E ,

где – диэлектрическая восприимчивость среды;

99

0 – диэлектрическая постоянная;

Р – мгновенное значение поляризованности вещества. Отсюда квадрат показателя преломления вещества (среды) равен

n2 1 P / 0E .

Дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав диэлектрика. Под воздействием переменного электромагнитного поля волны, колеблющегося по гармоническому закону E Em cos t и

H Hm cos t , заряженные частицы совершают вынужденные колебания.

При описании этого явления анализируют колебания одного электрона в атомах вещества. Такое упрощение позволяет использовать в расчётах поляризованность вещества P в виде уравнения

P n0 p n0ex ,

где n0 NVA – концентрация атомов в диэлектрике;

e– электрический заряд электрона;

x – смещение электрона от равновесия под воздействием элект-

рического поля Е световой волны. Подставив значение Р, получают

n2 1 n0ex / 0E ,

где Е – напряжённость электрического поля световой волны колеблющаяся по закону E Em cos t .

Поэтому дифференциальное уравнение вынужденных колебаний электрона без учета силы сопротивления приобретает вид:

где Fm eEm – амплитудаколебанийсилы, действующейнаэлектронсосто-

роны поля волны;0 – собственная частота колебаний электрона;

– частота внешнего поля; m – масса электрона.

Решениеданногодифференциальногоуравнениядлясмещенияэлектрона в виде x x t , подставляют в уравнение для п2, откуда квадрат пока-

зателя преломления вещества и показатель преломления вещества равны

100