2408

4.2. Типы конечных элементов

При выполнении расчётов пластин методом конечных элементов важную роль при формировании матрицы жёсткости конечно-элементной модели играет выбор типа конечного элемента.

Тип элемента характеризуется в первую очередь:

Ещё большее число разновидностей элементов существует в зависимости от:

набора узловых переменных, среди которых могут быть как перемещения, углы наклоны поперечных сечений, так и усилия на контуре элемента, характеризующие его состояние, т.е. числа степеней свободы (ср.

41

например, на рис. 4.2 схемы «а» и «б» треугольных элементов с разным количеством узлов);

способа аппроксимации поля перемещений деформированного элемента с помощью базисных функций;

класса рассматриваемых задач.

При первоначальном изучении МКЭ пластин достаточно ограничиться рассмотрением конечных элементов треугольной формы, таких, как:

1)плоский симплекс-элемент (элемент с постоянными деформациями –

СST);

2)элемент Морли.

Они могут быть использованы в расчётах пластин с прямолинейным и криволинейным очертаниями как внешнего, так и внутренного контура.

Плоский симплекс-элемент предназначен для расчёта пластины, нагруженной силами, расположенными в её плоскости. Элемент Морли, а также подобный ему элемент BCIZ, элемент DKT и четырёхугольные конечные элементы, исследованные в специальной литературе, находят широкое применение в расчётах изгибаемых пластин [3, 6, 7].

Обширные библиотеки конечных элементов имеются во всех вычислительныхкомплексах(ПК«Лира», SCAD идр.). КаждомутипуэлементавПК присваиваетсяопределённый номер иликоддля того, чтобыприразработке алгоритма программы расчёта пластинки по МКЭ необходимый элемент вместе с его ячейкой жёсткости можно было «вызвать» из библиотеки и вставить в программу.

Далее подробно рассматривается напряжённо-деформированное состояние двух простейших типов конечных элементов пластин, составляющих библиотеку элементов.

4.3.Ячейки жёсткости плоских элементов

Вэтом подразделе рассматриваются процедуры формирования ячеек жёсткости двух наиболее распространённых типов КЭ: симплекс-элемента

иКЭ Морли.

А) Двумерный симплекс-элемент с шестью степенями свободы

Дискретизацию диска при наличии криволинейной части контура целесообразно выполнять путём разбиения его на треугольные элементы (рис. 4.3,а). В таком случае в качестве конечного элемента служит пластинка треугольной формы с узлами в её вершинах – симплекс-элемент (рис. 4.3,б, в).

Узлы на плоскости х0у нумеруют, начиная с произвольно выбранного i-го узла, обходя треугольник против хода часовой стрелки. Абсциссы i-го, j-го и k-го узлов обозначают через хi , xj , xk , ординаты – через yi , yj , yk .

42

помощью которых описывается возможное распределение перемещений по полю элемента вдоль направлений осей координат, принимают линейными (в виде линейных полиномов):

а

б

в

Рис. 4.3

43

– матрица координат вершин треугольника.

Компоненты вектора , в частности коэффициент 0 , можно найти по способу Крамера

где K = 2А, буква А, как принято, обозначает площадь треугольника.

Разложив определитель, стоящий в числителе, по первому столбцу, определяют коэффициент

0 ui xj yk xk y j u j хi yk xk yi uk хi y j xj yi .

2A

Аналогично находят и два других коэффициента. После подстановки

44

Очевидно, величины i , i являются проекциями на оси 0x и 0y стороны j k треугольника, расположенной напротив i-й вершины (рис.

4.4). Распределение перемещений вдоль оси 0у находится по аналогии с определением перемещений u

если воспользоваться обобщённым вектор-столбцом узловых перемещений

фигурирующих в формулах (4.3). Указанные функции, очевидно, также носят линейный характер, что и функции u, , изначально принятые для

описания предполагаемого поля перемещений конечного элемента.

В МКЭ часто, минуя начальный этап, описанный выше, задаются изменением перемещений в форме (4.4), выбирая базисные функции, соответствующие критериям полноты и совместности деформаций*. В рассматриваемом случае в качестве базисных функций можно взять функции, принимающие единичное значение в одном из узлов конечного элемента

* Критерий полноты, в частности, заключается в том, что базисные функции должны обеспечивать

описание НДС в области КЭ, соответствующего случаю постоянных деформаций и напряжений пластинки; при этом выполняется равенство Li + Lj + Lk = 1. Совместность выражается в сохранении непрерыв-

ности как самих функций, так и их производных, встречающихся в выражении потенциальной энергии конечного элемента.

45

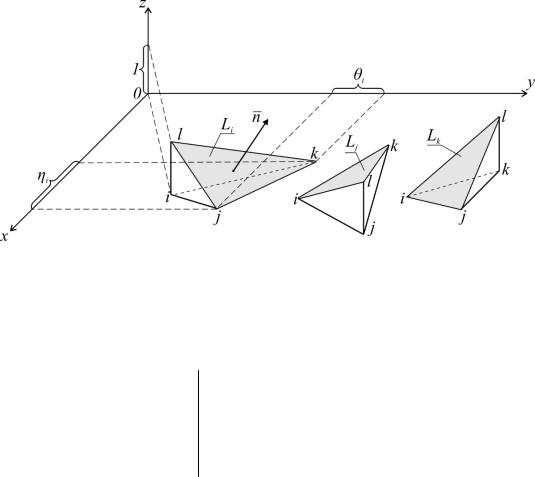
при сохранении нулевых величин в двух других. Графической иллюстрацией одной из таких функций, например для i-й вершины

треугольника, служит наклонная плоскость Li x, y , след которой на

горизонтальной плоскости х0у совпадает с прямой, проходящей через вершины j, k треугольника и через точку l, расположенную над вершиной i на расстоянии, равном единице (рис. 4.4).

Рис. 4.4

Указанным признакам плоскости Li x,y в аналитической форме отвечает условие равенства нулю определителя следующей структуры [12]:

Разложив определитель по третьему столбцу и заменив при этом z на Li x, y , легко вывести уравнение

которое в явной форме принимает вид

46

где, как и в формулах (4.6,а), присутствуют проекции i , i и удвоенная площадь треугольника, равная

Однако, в отличие от функции Ni x, y , в полученной формуле для Li x,y отсутствует слагаемое, содержащее постоянную величину i .

Аналогично находятся базисные функции и для двух других узлов (см.

рис. 4.4):

Наклон плоскости с осью абсцисс составляет угол i arctg i 2A . С

учётом этих замечаний выражение для функции Li x, y принимает вид

Li x, y хtg i ytg i .

По аналогии записываются и другие базисные функции.

Рис. 4.5

47

Таким образом, обобщённое поле перемещений можно выразить и с помощью новых функций согласно преобразованию (4.4), в котором

матрица N подлежит замене на матрицу

похожей структуры.

Вектор деформаций ε x , y , xy , компоненты которого находятся на основе общих соотношений между деформациями и перемещениями

справедливыми в рамках плоской задачи теории упругости, можно представить в матричной форме

если воспользоваться матричным дифференциальным оператором следующего вида:

Учитывая зависимость (4.4), несложно установить связь между деформациями и узловыми перемещениями

= L Z .

Произведение матриц в этом выражении, обозначаемое символом

называется матрицей формы деформаций или матрицей градиентов; в литературе на английском языке – «strain matrix». С её помощью вектор деформаций пластинки можно представить в виде

Структуру матрицы В легко установить, выполнив перемножение матриц и L и последующее дифференцирование выражений (4.6,б)

48

Матрица формы деформаций позволяет найти деформации конечного элемента на основе перемещений его узлов. Так как все элементы блоков

данной матрицы постоянны, то и компоненты вектора деформаций ε на всей площадкерассматриваемого конечного элементапостоянны (критерий

полноты базисных функций Li x, y , Lj x, y , Lk x, y удовлетворяется).

Если в последних выражениях выполнить умножение, то они могут быть представлены через тангенсы углов наклона плоскостей

Li x, y , Lj x, y , Lk x, y с осями координат:

матрица H , связывающая узловые перемещения с деформациями эле-

ментов стержневой системы [11].

Зависимость между напряжениями и деформациями для изотропных упругих пластин подчинена закону Гука

x , y , xy T D ,

где

– матрица упругих констант (матрица упругости) пластины; E, – модуль

упругости и коэффициент Пуассона материала пластины. Когда здесь

Е0 1 E 2 , 0 1 ,

49

имеет место случай плоского напряжённого состояния ( z = 0 ), а при

Е0 = E, ν0 = ν – плоской деформации ( z 0 ).

Приняв во внимание выражение для деформаций согласно (4.9), напряжения в элементе можно определить через узловые перемещения, т.е.

Выражения энергии упругих деформаций и работы внешних распределённых нагрузок интенсивностью q , приложенных на контуре в срединной

плоскости конечного элемента, с учётом последних соотношений можно представить в матричном виде:

После подстановки выражений для энергии W и работы А в условие минимума полной потенциальной энергии элемента

W A 0Z

с последующим дифференцированием матричных произведений в соответствии с правилами:

уравнение равновесия конечного элемента можно записать в матричной форме, а именно

50