2545

12 10 6 K 1. 0 C 273,15 K , где К – кельвин, единица измерения

температуры.

Знаки членов формулы (3.55) определяются так: если деформации элемента dx от температуры и от единичной силы аналогичны, то знак соответствующего члена будет положительным, и наоборот. Т.е. положительные знаки будут тогда, когда изгибающие моменты Mm (и продольные

силы Nm ) фиктивного состояния вызывают одинаковые деформации воло-

кон с температурными деформациями стержней.

Пример 1. Отыскать горизонтальное перемещение точки С (рис.3.29), если внутри температура повысилась на 10 С. h=0,2 м.

Рис. 3.29

Решение. По направлению искомого перемещения прикладываем силу P 1 и строим единичные эпюры M и N (рис.3.29, б, в).

M 12 3 3 3 3 4,5 9;N 1 3 3.

Температурные множители

(t1 t2 ) (0 10) 10;

(рис.3.30,а), если внутри температура повысилась на 20 С. Высота сечений стоек – 0,4 м, высота сечения ригеля – 0.5 м.

71

Решение.

Рис. 3.30

1093,75 400 60 1553,75 м.

3.9.Перемещения статически определимых систем, вызываемые осадкой опор

Встатически определимых системах осадки опор не вызывают реакций во внутренних связях, то есть не вызывают внутренних усилий в элементах системы.

Пусть требуется определить какое-либо перемещение в статически определимой системе, у которой опора получила перемещение 1 и 2

(рис.3.31,а).

Рис. 3.31

72

Приложим в точке, перемещение которой определяется, единичную силу P 1 в направлении искомого перемещения i и найдем опорные

реакции в заданной системе (рис. 3.31,б).

На основе принципа возможных перемещений можно записать, что если система находится в равновесии, то сумма элементарных работ всех активных равна нулю:

Произведения под знаком суммы имеют знак плюс, если направления перемещения совпадают с направлением реакции. В противном случае – наоборот – знак минус.

Пример . Требуется определить перемещение точки К в статически определимой системе, у которой опора получила перемещение С1, С2 и С3. (рис.3.32). С3 0,1 рад; С1 0,05 м; С2 0,03 м.

Рис. 3.32

HB 1; RA 142 0,5; RB 0,5; M B 1 2 0,5 8 6. P1 1c M B C3 HB C1 RB C2 0.

1c M B 0,1 HB 0,05 RB 0,03 6 0,1 1 0,05 0,5 0,0030,6 0,05 0,015 0,65 0,015 0,635 м.

2с 8 0,1 1 0,05 1 0,03 0,82 м.

73

4. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ СИЛ

Метод решения статически неопределимых задач, при котором за неизвестные принимаются усилия в лишних связях, или метод сил, появился давно. В неявном виде он фигурировал при расчете неразрезной балки уже в 1808 г.

Канонические уравнения метода сил впервые в литературе дал Максвелл в 1864 г. Он вывел эти уравнения для статически неопределимой фермы, пользуясь принципом возможных перемещений и рассматривая последовательно возможную работу сил X1=1, X2=1 и т.д. на действительных перемещениях системы.

Дальнейшее развитие эти уравнения получили в 70-80-х гг. XIX в. в трудах Мора и ряда других авторов. В России проф. В.Л. Кирпичев познакомил широкий круг инженеров с общей теорией расчета статически неопределимых стержневых систем в конце

XIX — начале XX в.

Особое внимание канонические уравнения метода сил стали привлекать к себе тогда, когда возникла необходимость рассчитывать сложные, т.е. содержащие много лишних неизвестных, и притом весьма разнообразные по своим формам и геометрической структуре статически неопределимые системы.

4.1. Основная идея метода

Рассмотрим задачу расчета статически неопределимой системы на примере балки, изображенной на рис.4.1,а.

Рис. 4.1

74

Данная балка 1 раз статически неопределима, т.к. для закрепления одного диска требуется три связи. Поэтому реакции не могут быть определены из уравнений равновесия. Отбросим «лишнюю» связь в опоре В и заменим ее неизвестной реакцией X1 . Система с отброшенной связью

(рис.4.1,б) является статически определимой. Система с отброшенными лишними связями называется основной системой.

В основной системе можно определить перемещение точки приложения силы X1 по направлению этой силы от внешней нагрузки Р (рис.4.1,в), равное

1p , а также перемещение силы X1 1 по своему направлению, равное 11 . Полное перемещение от силы X1 будет равно 1X 11 X1 . Ввиду отсутствия вертикального перемещения т.В в заданной системе мы должны записать

Остальные реакции легко определяются из уравнений равновесия, после чего можно построить эпюры внутренних усилий и найти напряжения в любой точке любого сечения балки.

4.2. Лишние неизвестные. Выбор основной системы метода сил

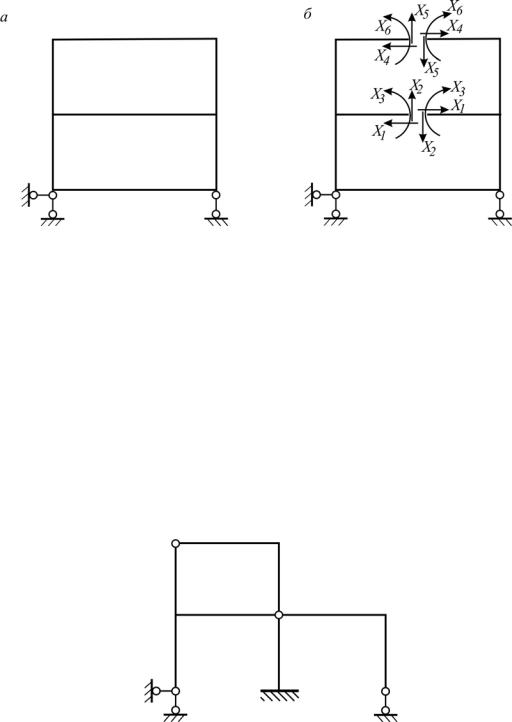
Первым вопросом, возникающим при анализе статически неопределимой стержневой системы, является вопрос определения числа лишних связей. В качестве лишних связей могут (рис.4.2,а) выступать как реакции опорных связей (рис.4.2,б), так и реакции внутренних связей (рис.4.2,в).

Рис. 4.2

Для определения лишних связей обычно используют два подхода. Первый из них состоит в применении основной формулы кинематического анализа сооружений:

75

Второй подход основывается на том очевидном факте, что каждый замкнутый контур является трижды статически неопределимым (рис.4.3).

Рис. 4.3

Следовательно, если рассматривается произвольная многоконтурная рама, то степень ее статической неопределимости, т.е. число лишних связей можно вычислить по следующей формуле:

где K – количество замкнутых контуров;

СОТ – число связей, недостающих для полного замыкания контура.

На примере для рамы, показанной на рис. 4.4,

W 3D 2Ш C0 3 4 2(1 3) 6 2 ,

или

3K COT 3 3 (1 1 3 2) 2 .

Рис. 4.4

При выборе основной системы надо следить за тем, чтобы она не оказалась геометрически изменяемой. Вообще же вариантов основной системы может быть несколько. Например, для рамы, изображенной на рис.4.5,а, число лишних неизвестных равно:

3K COT 3 2 (2 1 1 1) 1.

76

Здесь первые индексы означают направление перемещения (и номер отброшенной связи), а вторые указывают причины, вызвавшие перемещения.

Обозначив реакцию связи k через Xk и выразив перемещение ik через единичные перемещения с помощью равенства ik Xk ik , представим условие (4.5) в виде:

Таким образом, условие эквивалентности основной и заданной систем математически сводится к удовлетворению системы n линейных уравнений:

Первое уравнение выражает мысль о равенстве нулю перемещений в основной системе по направлению первой отброшенной связи, второе – по направлению второй отброшенной связи и т.д.

Уравнения (4.7) называют каноническими уравнениями метода сил, т.к.

они составлены по определенному правилу (канону). Неизвестными здесь являются реакции отброшенных связей. Эти уравнения можно записать в

Коэффициенты 11, 22 ,..., nn называют главными коэффициентами, а остальные – побочными. Т.к. ik ki (см. теорему о взаимности перемещений), матрица L является симметрической.

78

4.4. Вычисление коэффициентов и свободных членов канонических уравнений и их проверка

Для рам и балок, работающих преимущественно на изгиб, коэффициенты и свободные члены канонических уравнений метода сил могут быть вычислены по формулам:

Для этого в основной системе предварительно строятся эпюры изгибающих моментов Mi от Xi 1 и эпюра изгибающих моментов от внеш-

ней нагрузки M p . Эпюры Mi называются единичными, а эпюра M p –

грузовой.

Главные коэффициенты ii всегда положительны, а побочные члены

могут иметь как положительные, так и отрицательные связи.

После вычисления коэффициентов обычно делается их проверка по формуле:

4.5. Построение окончательных эпюр внутренних усилий.

Статическая и кинематическая проверка

Итак, система уравнений построена и проверена. После ее решения тем или иным способом и определения значений лишних неизвестных X1, X2 ,..., Xn строятся исправленные эпюры Mi Xi .

Окончательная эпюра моментов определяется сложением

i 1

После этого строятся эпюры поперечных Q и продольных N сил.

79

Правильность окончательной эпюры М проверяется с помощью

кинематической проверки:

Физический смысл этой проверки таков: сумма перемещений по направлению всех отброшенных связей должна быть равна нулю.

Статическая проверка заключается в условиях равновесия моментов в жестких узлах и в равенстве нулю проекций сил Fkx 0, Fky 0 в

раме, отсеченной от опорных закреплений.

4.6. Примеры расчета

Пример №1. Рассчитать раму (рис.4.7,а) методом сил. Решение. Подсчитаем степень статической неопределимости рамы:

W 3 Д 2Ш Соп 31 2 0 4 1,

т.е. данная рама один раз статически неопределима. Выберем основную систему, отбрасывая одну связь (рис. 4.7,б) и заменяя ее действие неизвестной силой Õ1 . Уравнение метода сил имеет вид

11X1 1p 0 .

Уравнение метода сил примет вид

X1 E72I EI66 0,

откуда

Строим исправленную эпюру М1 X1 (рис. 4.8,а). Окончательная эпюра

моментов (рис. 4.8б) соответствует уравнению

Mок M p М1 X1.

80