2545

3.5. Определение перемещений. Интеграл Мора

Вопрос о простом, а главное, общем способе определения перемещений – центральный вопрос теории статически неопределимых систем. Отсутствие общей формулы перемещений было главным препятствием, о которое в течение долгого времени разбивались попытки построения общего метода расчета статически неопределимых систем. Существенный шаг к решению расчета арки был сделан Максвеллом. Он впервые определил как работу взаимное сближение двух точек фермы, вызванное заданным удлинением s одного из ее стержней. Уравнение работ, которое до Максвелла служило средством для нахождения усилий, после него стало инструментом для вычисления перемещений. Это открыло новую страницу в строительной механике.

Рассуждения Максвелла заключают в себе некоторое ограничение, обусловленное тем, что он применил принцип возможных перемещений не в общем, а в частном виде – в форме принципа сохранения энергии. Написанное им уравнение работ справедливо только в том случае, когда удлинение s обусловлено именно силами Р, приложенными по направлению искомого перемещения. Но как быть в том случае, когда заданы удлинения нескольких стержней? В этом случае невозможно приложить такие две силы, которые вызовут во всех стержнях заданные удлинения. Здесь приходится прибегнуть к опыту предшественников.

В период 1874-1885 гг. Мор в ряде работ дал для фермы более прямое решение, так как исходил непосредственно из принципа возможных перемещений и учел влияние не только внешней нагрузки, но и температуры.

Распространение общей формулы перемещений на элементы, работающие на изгиб, содержится в книге Кастилиано, изданной в 1875 г., где эти перемещения написаны в форме производной от потенциальной энергии стержневой системы.

К концу 80-х гг. прошлого века общая формула перемещений стержневых систем была доведена до такого совершенства, которое было необходимо для ее действенного применения в практике инженерных расчетов. Однако потребовалось еще немало времени, чтобы в строительной механике она заняла подобающее место. Постепенно все частные способы вычисления перемещений, применявшиеся для различных систем, уступили место общей формуле.

Рассмотрим два состояния упругой системы. В первом состоянии на нее действует какое угодно число сил и моментов.

1-е состояние – действительное загружение

2-е состояние – единичная (фиктивная) нагрузка

Рис. 3.10

61

Во втором состоянии к системе приложена лишь одна сосредоточенная

сила Р2 1.

Работа силы Р2 на перемещении 21, возникающем от сил первого состояния, равна:

усилия вызваны действием единичной силы.

Таким образом, формула (3.41) позволяет найти перемещение от любой нагрузки. Для определения перемещения надо в направлении искомого перемещения данной точки конструкции приложить единичную силу. Далее следует определить внутренние усилия от заданной нагрузки и от единичной силы. Перемещение по направлению силы Pm 1, вызванное

заданной нагрузкой n, определяется по формуле Мора (или с помощью интеграла Мора):

Если требуется определить поворот данного сечения mn , то вместо единичнойлинейнойсилывсеченииприкладываетсяединичныймомент Mm 1.

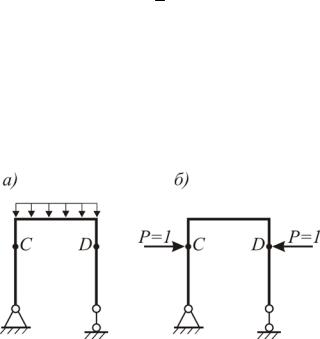
Если определяется взаимное сближение точек конструкции (рис.3.11а, точки С и D), то следует в точках С и D (рис.3.11б) приложить единичные силы, направленные по линии CD.

Рис. 3.11

При практическом использовании формулы Мора для изгибаемых систем оставляют только первое слагаемое, для систем, работающих на растяжение-сжатие, используют только второе слагаемое.

62

3.6.Вычисление интеграла Мора по правилу Верещагина

Всистемах, состоящих из прямолинейных элементов постоянной жесткости, определение перемещений можно значительно упростить, используя

l

специальный прием вычисления интеграла вида MmMndx. Этот приём

0

называют перемножением эпюр способом Верещагина (по фамилии студента Московского института железнодорожного транспорта А.К. Верещагина предложившего это правило в 1925 году). Его можно использовать, если одна из эпюр, например Mm , прямолинейна.

Рис. 3.12

63

Тогда

Т.е. результат перемножения двух эпюр равен произведению площади одной из них на ординату yc другой (прямолинейной) эпюры, взятую под

центром тяжести площади первой эпюры. Ордината yc должна быть

взята обязательно из прямолинейной эпюры.

Когда перемножаются две эпюры, имеющие вид трапеции, то следует одну из эпюр разбить на два треугольника

Для «перекрученных» трапеций эта формула сохраняет свой вид, но с учетом знаков перемещений

Когда перемножаются две эпюры, ограниченные ломаными линиями, то целесообразно разбить их на участки, где легко определить положение центра тяжести или можно использовать формулу перемножения трапеций.

64

При

Рис. 3.21

3.7. Определение перемещений от силовых воздействий

Пример №1. Вычислить вертикальное перемещение конца консоли (рис 3.22).

Изгибающий момент от внешней нагрузки:

Изгибающий момент от единичной силы:

M P l x .

Перемещение конца консоли равно:

66

Пример №2. Определить вертикальное и горизонтальное перемещение точки К, используя метод Верещагина (рис. 3.23,а).

Определим угол поворота в сечении I-I.

67

Пример №3. Найти горизонтальное перемещение крайней правой точки Т-образной системы (рис. 3.25,а).

Рис.3.25

На рис. 3.25,б показана грузовая эпюра, а на рис. 3.25,в – единичная эпюра. Горизонтальное перемещение системы (рис 3.25,г) равно:

Рис. 3.26

Грузовая и единичная эпюры показаны на рис. 3.26,б и 3.26,в, соответственно.

68

49,125 10 6 м.

Определим угол поворота сечения 1. Приложим в этом сечении единичный момент M 1. Построим эпюру изгибающих моментов от этого воздействия (рис.3.27).

3.8. Определение перемещений от температурных воздействий

Формулу Мора для стержней, испытывающих деформации изгиба и растяжения (сжатия) можно записать в виде

69

В таком виде формула Мора может быть использована, когда деформации d n и d n элемента dx стержня вызваны не только внутренними

усилиями в поперечных сечениях от нагрузки, но и действием температуры на сооружение.

Рассмотрим стержень с высотой поперечного сечения h и с произвольно расположенным центром тяжести (рис.3.28).

Рис. 3.28

Пусть верхнее волокно элемента dx нагрето на t1 , нижнее – на t2

градусов Цельсия. Распределение температуры по сечению примем по линейному закону. Тогда удлинение верхнего волокна будет равно t1dx , а

нижнего – t2dx , где – коэффициент линейного расширения материала стержня. Продольная деформация будет определяться формулой

Деформация искривления, определяемая углом взаимного поворота

Для случая прямолинейных стержней постоянного сечения интегралы могут быть рассчитаны как площади единичных эпюр и формула перемещений примет простой вид:

70